This paper proposes a method for predicting the dispersion of reinforcement nanoparticles (TiC) within the molten pool during the DED (Direct Energy Deposition) additive manufacturing process for a metal matrix composite (Ti-6Al-4V). The formation behavior of the molten pool was computationally simulated using a Finite Volume Method (FVM)-based model that incorporates the Marangoni effect and complex physical phenomena. The cross-sectional analysis of the molten pool demonstrated that the prediction error was, on average, within 10% compared to the experimental values. Based on these predicted values, the behavior of the nanoparticles within the molten pool was simulated using the Discrete Phase Model (DPM), ultimately enabling the prediction of their dispersion within the molten pool.

본 연구에서는 나노 크기의 강화입자(TiC)가 포함된 금속기지복합재(Ti-6Al-4V)의 에너지 직접 용착(DED, Direct Energy Deposition) 방식 적층제조에서의 용융풀 내 강화 입자 분산 예측방법을 제시하였다. 마랑고니 효과(Marangoni effect) 및 복잡한 물리현상을 포함한 유한체적법(FVM, Finite Volume Method) 기반 모델링을 통해 용융풀 형성 거동을 전산 모사하였으며, 용융풀 단면 분석 결과 실험값 대비 평균적으로 10% 이내의 예측 오차율을 보임을 확인하였다. 이러한 예측 값을 기반으로 이상유동모델(DPM, Discrete Phase Model)를 이용하여 용융풀 내에서의 나노 입자의 거동을 모사하였고, 최종적으로 용융풀 내 분산을 예측하였다.

Keywords: 금속기지복합재(Metal Matrix Composites), 에너지 직접 용착(Directed Energy Deposition), 적층제조(Additive Manufacturing), Discrete Phase Model(DPM)

에너지 직접 용착(DED, Direct Energy Deposition) 방식은 금속 적층 제조 방법 중 하나로서, 다른 적층 제조 방법들에 비해 적층 가능한 부품의 크기가 크고, 적층률이 높다는 장점이 존재한다. 이러한 장점을 기반으로, 넓게는 항공우주분야에서 사용되는 기능성 부품 제작에서부터 복잡한 구조를 가지는 메타물질 및 여러 금속기지복합재(MMC, Metal Matrix Composites) 제작에 널리 활용되고 있다[1-3]. 그러나, 선택적 용융 방식(SLM, Selective Laser Melting)과 같은 다른 금속 적층 제조 공정들이 오랜 연구와 테스트를 통해 발전해온 것과 달리, 에너지 직접 용착 방식의 경우 비교적 새로운 기술로 아직까지 연구 개발이 충분치 않은 실정이다.
에너지 직접 용착 방식을 포함한 금속 적층 제조에 대한 연구는 주로 실험적으로 수행되어 왔다. 그러나 금속 적층 제조의 경우 실험에 소모되는 시간적, 금전적 비용이 크고 공정 상 발생하는 물리현상을 직접적으로 관찰하기 매우 어렵기 때문에, 수치해석을 활용하여 공정 상에서 발생하는 물리현상을 분석하는 시도들이 이어지고 있다[4-6]. 일반적으로 수치해석을 이용한 에너지 직접 용착 공정 해석 모델은 유한요소법(FEM, Finite Element Method)과 유한체적법(FVM, Finite Volume Method) 두 가지 모델로 구분할 수 있다.
유한요소법을 이용한 금속 적층 제조 공정의 전산 모사는 요소의 활성/비활성을 통해 구현된다. 파우더가 녹아 유입이 되기 전까지 적층 위치에 해당하는 요소가 비활성 상태로 유지되다가, 이후 레이저 에너지로 인해 요소의 온도가 녹는 점에 도달하면 요소가 활성화되고 열전도를 통해 에너지를 확산시킬 수 있도록 모델링 된다[4,7-10]. 이러한 유한요소법 기반 공정 해석은 유한체적법 모델에 비해 비교적 간단하고, 계산량이 적고 빠르게 결과가 도출된다는 장점이 있으나 용융풀 내에서 일어나는 각종 물리 현상이 무시되어 온도분포, 잔류 응력 및 변형이 제대로 모델링 되지 않는다는 단점이 존재한다.
유한체적법을 이용한 전산 해석의 경우 질량 보존 방정식, 운동량 방정식, 에너지 방정식을 전산유체해석(CFD, Computational Fluid Dynamics) 모델에 포함하여 비선형 편미분 방정식을 기반으로 유체의 운동, 확산, 그리고 상 변화와 같은 현상을 계산한다[11-13]. Gan et al.[14,15]은 단층 및 다층 레이저 클래딩(cladding) 중 적층 형상을 예측하기 위해 전산유체해석 모델을 개발하였으며, 마랑고니 효과(Marangoni effect)와 표면장력으로 인한 힘을 모델에 포함시켰다. 마랑고니 효과는 용융풀 형성 및 열유동 해석에 있어 중요한 현상 중 하나로, 두 상(phase) 간의 계면에서 표면장력 크기의 구배가 존재할 때 발생한다[16]. 유한체적법 모델에 포함되는 마랑고니 효과 및 다양한 복잡한 물리현상(레이저 반사, 반발압 등)은 용융풀 내 온도 및 유동 그리고 기하학적 특성을 더 정확히 계산할 수 있게 도움을 주지만, 계산 난이도를 크게 증가시켜 제한적으로 사용되고 있었으나 컴퓨팅 파워의 발전과 함께 용융풀의 정확한 형상 예측을 위해 필수적으로 모델에 포함되어 연구가 이루어지고 있다[17,18].
이러한 에너지 직접 용착 공정 모델링에 관한 연구와 더불어 기존에 저조했던 에너지 직접 용착 공정을 이용한 금속기지복합재 제조에 대한 연구가 최근 실험 연구 위주로 이루어지고 있다. Jiang et al.[19]은 에너지 직접 용착 공정을 통해 7075Al/TiB₂ 복합재 적층을 수행했으며, TiB₂가 불균일하게 분산되었음에도 4 wt% TiB₂ 함량에서 약간의 결정립 미세화가 달성된 것을 확인하였다. 또한 Wen et al.[20]도 DED 공정을 통해 2024Al/TiB₂ 복합재에서 비슷한 경향이 나타남을 관찰하였다. Pouzet et al.[21]은 Ti-6Al-4V/B₄C 복합재의 미세구조 및 기계적 특성을 연구하였다. 해당 연구에서 TiB의 바늘 구조로 인해 핵 형성 효과가 강화되었으며, 이는 낮은 B₄C 함량에서도 이러한 효과가 나타날 수 있음을 보여준다.
그러나, 이러한 연구들은 시간적, 비용적 소모가 큰 실험 위주로 진행이 되었다는 제한점이 존재한다. 특히 금속기지복합재의 경우 원료(feedstock) 개발이 제한적으로 이루어지기 때문에, 다양한 금속기지복합재에 대해 연구를 수행하기 위해서는 수치해석을 위한 전산 모델링이 필수적이다. 따라서 본 연구에서는 나노 크기의 강화입자(TiC)가 포함된 금속기지(Ti-6Al-4V) 복합재의 에너지 직접 용착 방식 적층제조 공정을 전산 모사하여 최종적으로 적층된 싱글 비드(Single bead)에 대해 강화입자의 분산을 예측하였다. 용융풀 형성 과정과 나노입자 분산 예측 과정을 이원화화여 유한체적법 기반 열 유동 모델을 통해 용융풀 형성 과정 및 유동 흐름을 분석하고, 이러한 데이터를 기반으로 이상유동모델(DPM, Discrete Phase Model) 방법을 적용하여 최종적으로 나노 입자의 분산을 예측하였다.

2.1 유한체적법 기반 용융풀 유동 해석
본 연구에서는 에너지 직접 용착 공정에서의 용융풀 유동을 해석하기 위하여 유한체적법 기반 열유동(Thermo-fluid) 해석을 수행한다. 효율적인 해석을 위해 다음과 같은 네 가지 가정을 설정하였다.
1) 용융풀 내 유동의 비압축성, 점성/층류 유동 가정
2) 용융 금속의 뉴턴 유체 가정
3) 연기(fume)의 생성 및 효과 무시
4) 금속 분말의 비산(spatter) 무시
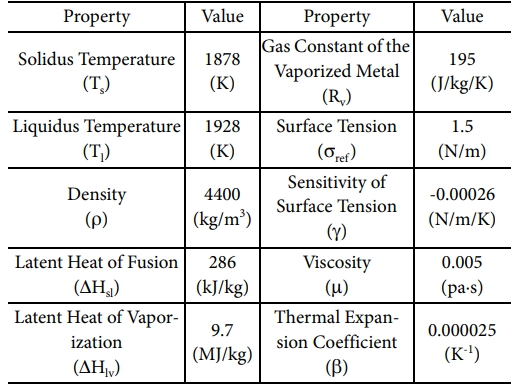
위 가정을 바탕으로 열유동 해석을 수행하였으며, 해석은 상용 코드인 Flow-3D를 사용하였다. 해석에 사용된 Ti-6Al-4V의 열물성은 Table 1과 같다.
2.1.1 Fluid Flow Model
CFD 모델의 계산 영역은 두 가시 상(Phase)로 구성되는데, 첫 번째 상은 주변 공기(air)이며 두 번째 상은 금속 영역이다. 이러한 다상 유동을 모사하기 위한 방법으로 Volume of Fluid(VOF) 방법을 사용하여 연속방정식 및 모멘텀 방정식을 기술하였다.



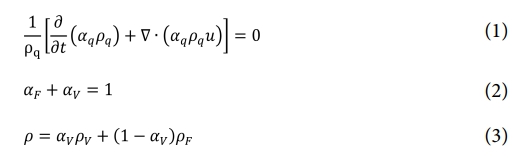
여기서 u는 유동장의 속도벡터이고, q는 각 상(phase)의 지시자로서 본 연구에서는 공기와 금속(Ti-6Al-4V)를 의미한다. a는 상의 부피분율으로 식 (2)와 같이 유체상(금속, F로 표기)과 공극상(공기, V로 표기)의 부피분율 합은 1을 만족하여야 한다. 또한 수송 방정식(transport equation)에 사용되는 물성 값은 식 (3)과 같이 각 검사 체적(control volume) 내의 2차 상의 부피 분율에 의해 계산되었다. 식 (3)은 2상 유동에서의 유효 밀도를 나타낸 식이고, 다른 물성치도 같은 방식으로 계산되었다.



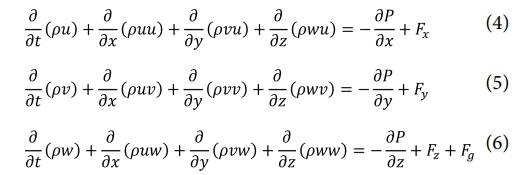
식 (3)~(6)은 모든 상의 합성 물성에 기반한 운동량 방정식으로, (u, v, w)는 유동장 속도 벡터 u의 x, y, z 성분이다. F항은 점성 응력을 나타내며 식 (7)과 같이 계산된다. 또한 공정 중 온도 변화에 의해 용융 금속의 밀도가 변화하며 발생하는 부력은 유체의 비압축성을 가정하여 Boussinesa approximation을 사용, 식 (8)과 같이 계산하였다.



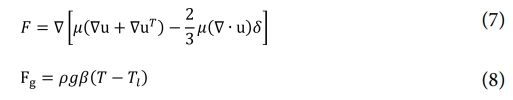
여기서 β는 금속의 열팽창 계수, T_l은 금속의 액상선 온도이다.
또한 용융풀의 자유표면에 작용하는 반발압(Recoil pressure), 용융풀 내의 온도 구배로 인해 압력이 발생하는 Marangoni 효과, 냉각과정 중 발생하는 표면장력 등의 요인들도 다음과 같이 고려되었다.



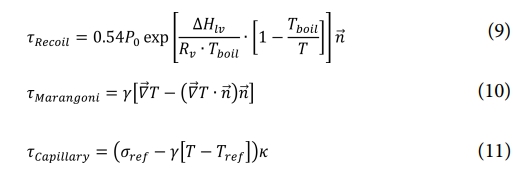
이 때 ∆H_lv는 증발 잠열, R_V는 기화된 금속의 기체 상수이다. σ_ref와 γ는 각각 기준 표면 장력(reference surface tension)과 온도에 따른 표면 장력 민감도(sensitivity of surface tension)를 나타낸다.
2.1.2 Heat transfer Model
본 연구에서 용융풀 계산 영역에 대해 적용된 에너지 방정식은 다음과 같다.



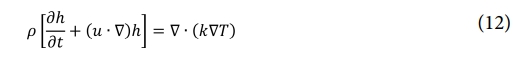
이 때 h는 엔탈피이고, k는 금속의 열전도율이다. 유체의 엔탈피는 식 (13)과 같이 표현 가능하다.



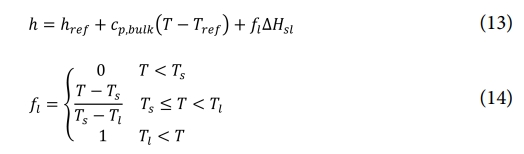
식 (13) 에서 c_p,bulk, ∆H_sl, 그리고 fl은 각각 비열(specific heat capacity), 융해 잠열(latent heat of fusion), 그리고 액체 분율 함수(liquid fraction function)이다. T_s는 금속의 고상선 온도이다. 또한 Rule of Mixture를 이용하여 비열은 식 (15)와 같이 계산된다.



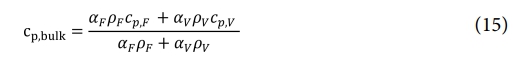
고 에너지 열원으로 인해 용융풀에서는 복사, 전도, 대류 및 상변화를 포함한 다양한 열 전달이 발생한다. 이러한 물리적 현상을 반영하여 다음과 같은 열 경계 조건을 설정하였다.



여기서 ε는 방사율(emissivity), η는 스테판-볼츠만 상수(Stefan-Boltzmann constant)를 나타낸다. ∆H_lv는 증발 잠열(latent heat of evaporation), T_boil은 끓는점, R_v는 기화된 금속의 기체 상수(gas constant)를 나타낸다.
2.1.3 Heat source model
본 연구에서는 레이저 열원의 반사 및 손실효과를 고려하는 레이 트레이싱(Ray-tracing) 방법이 적용되었다.
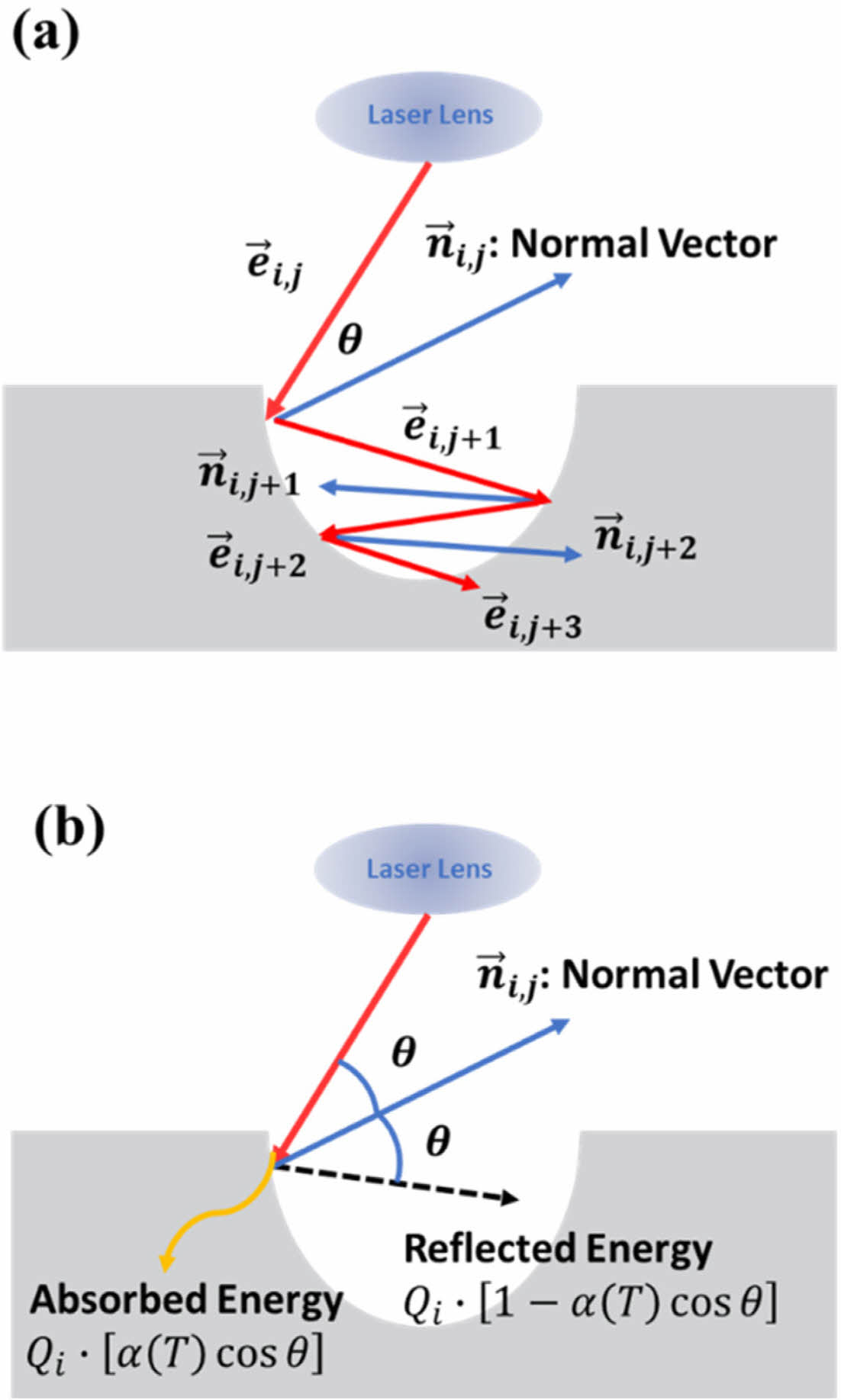
Fig. 1과 같이 레이저 레이는 용융풀 내에서 반사 및 흡수가 발생하게 되고, 그에 따라 용융풀에 전달되는 에너지에 변화가 발생한다. 이러한 레이저 레이를 추적하고 에너지를 계산하기 위해 식 (21), 식 (22)을 이용한다.



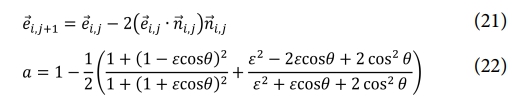
식 (21)은 레이의 반사를 추적하는 식으로 i는 각 레이저 레이에 대한 태그이고, j는 레이저 레이와 유체의 자유 표면이 충돌한 횟수를 나타낸다. 식 (22)는 프레넬 반사 모델(Fresnel reflection model)로 유체에 의해 흡수되는 에너지 양을 결정하는 유체의 흡수율(absorptivity) a를 식(18)에 따라 계산되는 레이의 각도를 이용하여 도출한다. e의 경우 특정 레이저 유형과 재료에 대해 그 값이 이미 결정되어 있는 것으로 알려져 있다. 본 연구에서는 0.2를 적용하였다.
2.2 이상유동모델 기반 강화입자 추적
2.2.1 이상유동모델
금속 기지 복합재를 사용한 에너지 직접 용착 공정 중에는 강화입자가 용융풀의 유동을 따라 용융풀 내에 분산된다. 강화입자는 용융풀 내에서 항력, 관성력, 중력 등과 더불어, 열영동력과 브라운력에 의한 영향을 받는다. 이상유동모델 해석에서 강화 입자에 대한 동적 지배방정식은 다음과 같은 수식으로 표현할 수 있다.



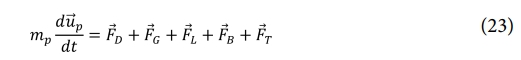
여기서 m_p는 입자의 질량이고, 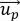는 분말의 속도이며, 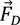, , 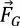, 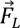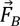그리고 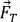는 각각 항력, 부력, 양력, 브라운력(Brownian force), 열영동력(Theromphoretic force)이다.
마이크로 크기 이상의 입자와 달리, 나노입자의 경우 작은 크기로 인해 열영동력(Thermophoretic force)과 브라운력(Browian force)가 추가적으로 작용한다. 여기서 열영동력이란, 온도 구배가 존재하는 용융풀 내에서 나노입자와 충돌하는 금속 원자들의 운동 에너지 차이로 인해 발생하는 힘으로, 나노입자가 고온영역에서 저온영역으로 이동하게 만든다. 그 수식적 표현은 다음과 같다.



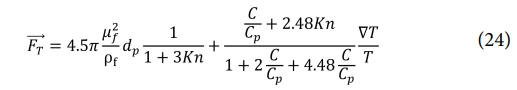
이 때 μ_f와 ρ_f는 용융 금속의 점성과 밀도이며, d_p는 강화입자의 직경이다. 또한 C와 C_p는 각각 용융 금속과 강화입자의 열전도도이다. Kn은 Knudsen 수로, 용융 금속 원자의 평균 자유경로와 강화입자의 직경을 통해 계산된다. 열적 요동(fluctuation)에 의해 나노 입자에 작용하게 되는 브라운력은 일반적으로 수식 (25)와 같이 확률적 힘(Stochastic force)로 표현된다.



여기서 R_i는 평균이 0이고, 분산이 1인 독립적인 가우시안 난수로 강화입자에 작용하는 힘의 벡터를 결정한다. 그리고 k_B, μ_f, d_p, T는 각각 볼츠만 상수(Boltzmann constant)와 기지의 점성, 강화 입자의 직경, 유체(기지)의 온도이다. C_c는 커닝햄 보정계수(Cunningham correction)으로 나노 및 마이크로 크기의 미세입자와 유체의 상호작용을 설명할 때 사용되는 계수이다. 이러한 작은 크기의 미세입자에서는 유체 내에서 완전한 점성 흐름을 따르지 않고 미끄러지는 슬립(Slip)이 발생한다. 커닝햄 보정계수는 다음과 같이 계산된다.



λ는 용융 금속 원자의 평균 자유 경로이며, d_p는 강화입자의 직경이다. A, B 그리고 C는 경험적 계수로 본 연구에서는 각각 1.257, 0.4, 0.55가 사용되었다.
기존 마이크로 크기 이상의 입자에 작용하는 항력, 관성력, 중력은 식 (27)~(29)과 같다.



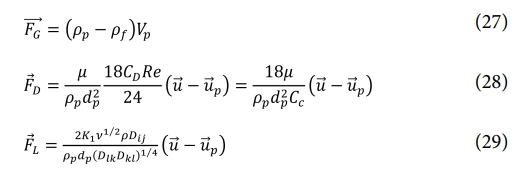
여기서 μ는 점도(viscosity), C_d는 항력계수(Drag coefficient), Re는 레이놀즈 수, ρ_p는 파우더의 밀도, d_p는 분말의 직경이다.
2.2.2 강화입자 생성 및 추적 알고리즘
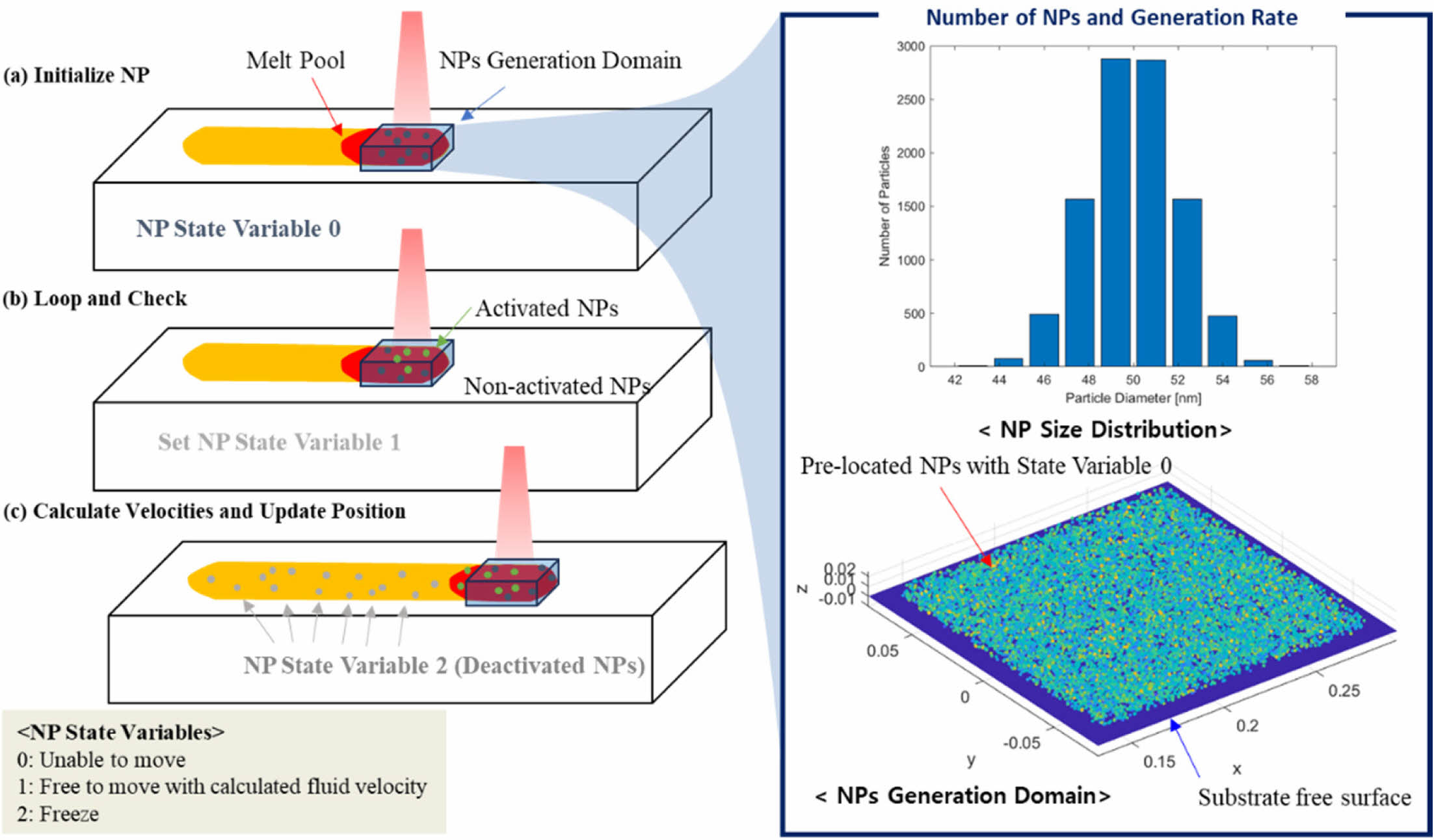
본 연구에서는 나노 크기의 강화 입자의 분산을 예측하기 위해 지배방정식에 기초하여, Fig. 2와 같은 나노 입자 생성 알고리즘을 인하우스 코드로 구현하였다.
a) Initialize Nano Particle(NP)
강화 입자가 생성될 영역을 지정한다. 해당 영역의 중심은 레이저의 조사 위치와 동일하며, 매시간 간격(time step)마다 레이저 이동에 따라 강화 입자 생성 영역 또한 업데이트한다. 생성된 강화 입자에 대해서는 상태변수(State Variables)를 지정하여 최소 생성시 0, 용융영역에 속하는 경우 1, 용융영역을 벗어난 경우 2로 강화입자를 구분한다.
b) Loop and check
CFD 결과로부터 생성된 나노 입자가 용융영역에 존재하는지 확인하여 상태변수를 업데이트한다.
c) Calculate velocities and update position
나노 입자의 운동 지배 방정식에 따라 매시간 간격마다의 속도를 계산하고, 위치를 업데이트 한다. 업데이트된 나노 입자가 용융영역에 존재하는지 판단 후 상태변수를 업데이트한다.

3.1 DED 용융풀 해석 결과
제시된 모델을 이용하여 200W-700mm/min, 200W-850mm/min, 300W-700mm/min, 300W-850mm/min의 네 가지 공정변수 조합에 대해 열유동 해석을 수행하고 실험 결과와 비교하였다.
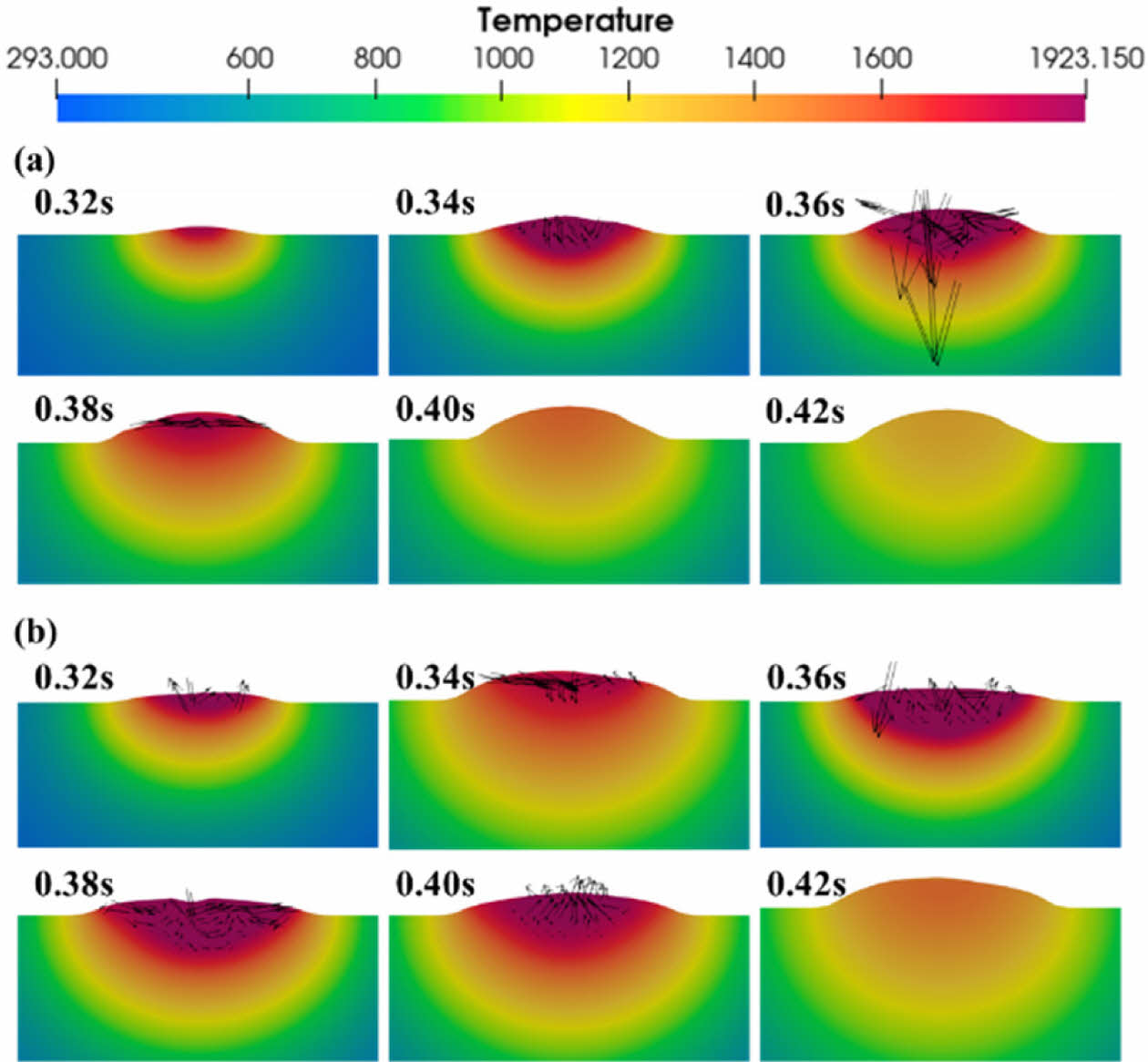
Fig. 3은 싱글 비드의 중앙 단면에서 레이저 진행 방향과 수직인 단면을 보여준다. 동일 시간에서 200W 조건 보다 고에너지인 300W 조건의 용융 정도는 더 크지만, 용융풀의 높이는 200W 조건에서 더 큼을 확인할 수 있다. 이는 높은 에너지밀도로 인해 고온에서의 표면장력 감소, 오랜 유동시간, 상대적으로 더 넓은 용융풀에서의 질량 분산이 복합적으로 작용한 결과로 볼 수 있다.
용융풀 내 유동 흐름 또한 확인하였다. 전반적으로 Fig. 3(b)의 0.38초에서 나타난 바와 같이 용융풀 상부에서는 유체가 중심에서 가장자리로 흐른 후, 용융풀의 가장자리를 따라 대각선 방향으로 아래쪽으로 이동하며, 마지막으로 0.4초에서와 같이 용융풀 바닥에서 위쪽으로 흐르는 순환 유동을 형성한다. 다만 파우더 유입으로 인해 Fig. 3(a)의 0.36초에서 나타난 바와 같이 때때로 강력한 하향 유동이 발생할 수 있음도 확인되었다.
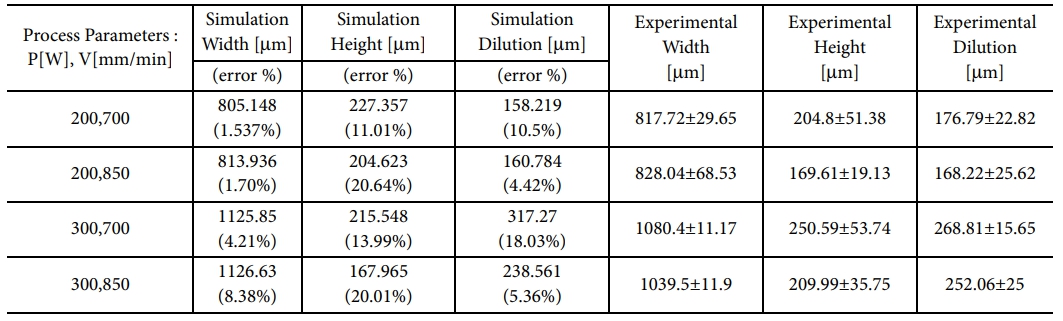
Table 2은 해석 결과를 실험결과와 비교한 표이다. 용융풀의 전체적인 형상이 대부분 10% 내의 오차를 보이며 높은 정확도로 예측되었다. 일부 Height 예측 결과가 실험값(평균치)과 20% 내외로 상대적으로 높은 오차를 보였으나, 이는 에너지 직접 용착 공정상 파우더 공급의 편차로 인해 발생하는 용융풀 크기의 큰 편차에서 기인한 것으로 보인다.
3.2 이상유동모델 해석 결과
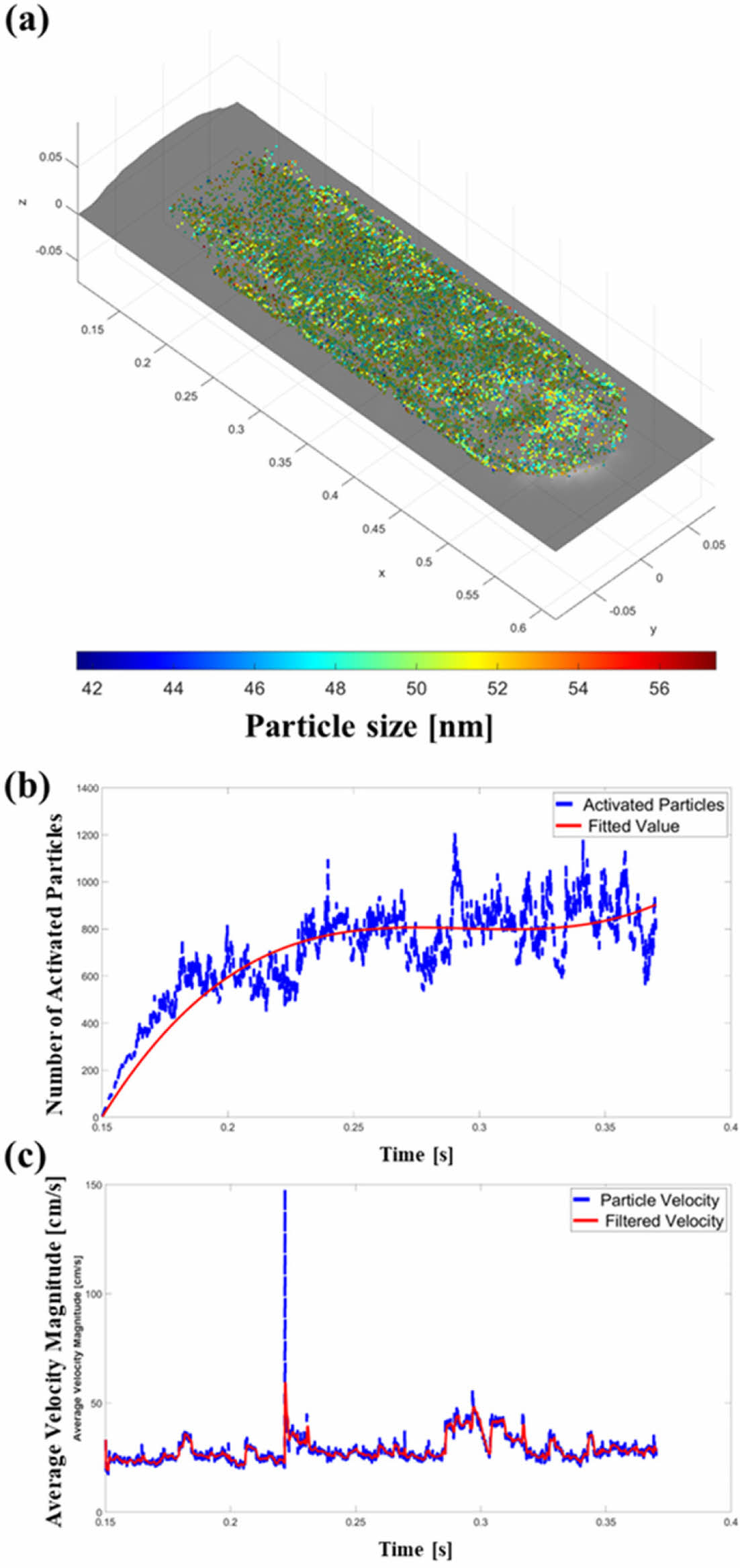
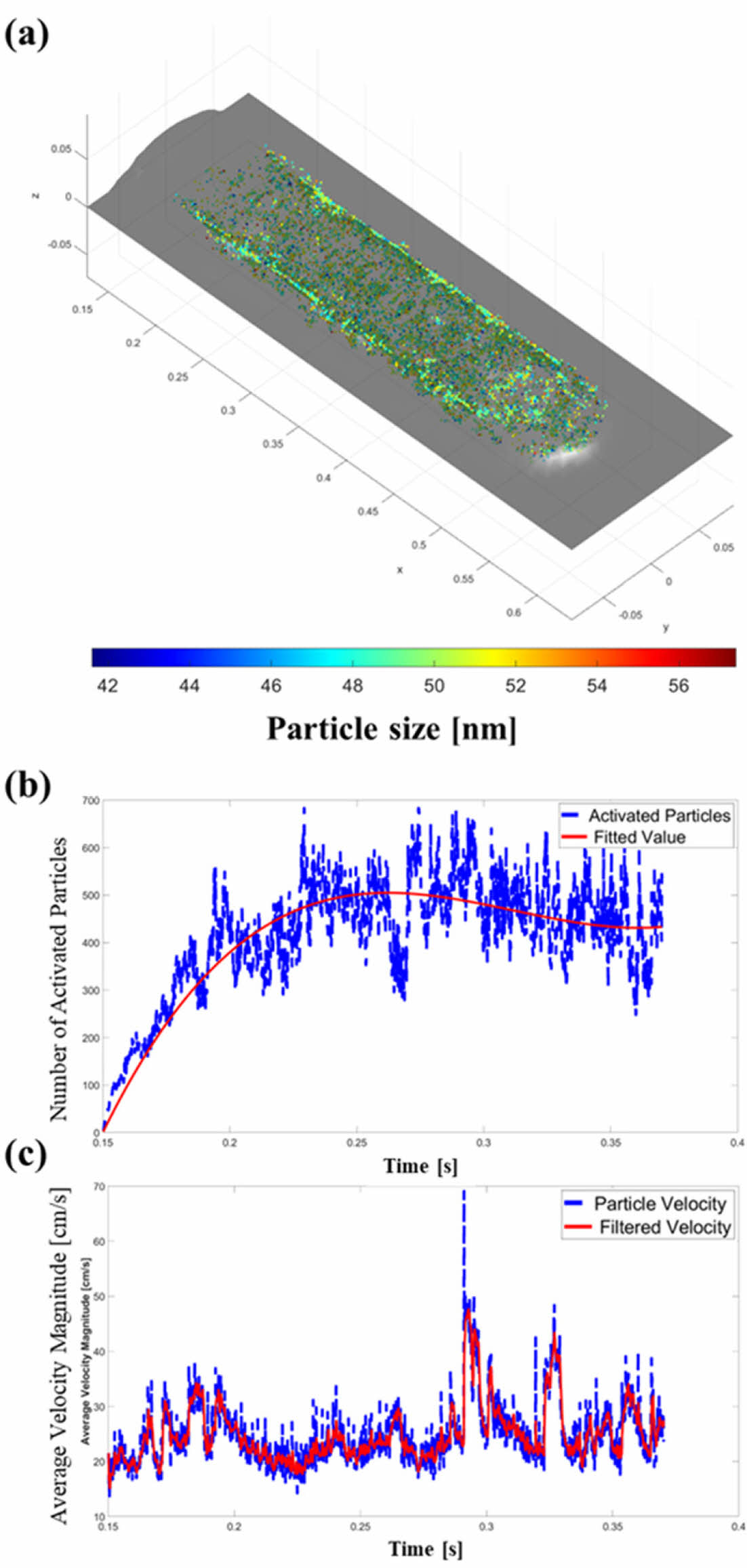
앞서 제시된 이상유동모델 알고리즘을 이용하여 200W-850mm/min, 300W-850mm/min의 두 가지 공정 조건에 대하여 강화입자 분산 해석을 수행하였다. 두 가지 조건에서의 해석 수행 결과는 각각 Fig. 4, Fig. 5와 같다. 각 그림의 (a)를 보면, 두 경우 모두 강화입자들이 용융풀 내의 유동을 따라 균일하게 분포하나, 200W-850mm/min 조건에서 조금 더 외곽에 밀집된 형태로 분포된 것을 확인할 수 있다. (b)에서도 마찬가지로 두 경우 모두 활성 강화 입자의 개수가 빠르게 증가하다가 0.25~0.3초경 수렴하수 시작하는 것을 확인 할 수 있다. (c)는 활성화 상태의 강화 입자의 평균 속도로, 두 조건 모두에서 약 25cm/s로 동일하게 나타났다.
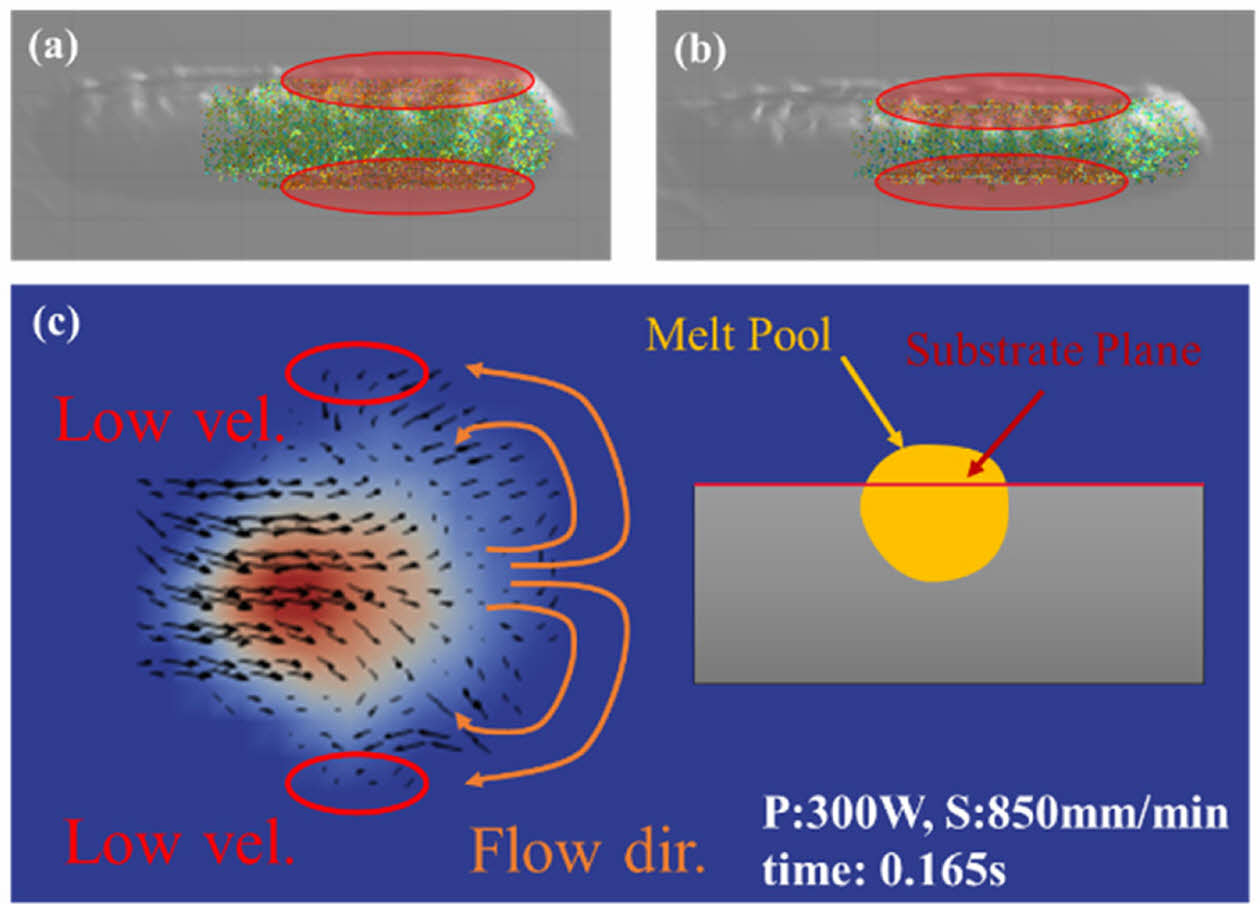
Fig. 6(a), (b)를 보면 두 가지 조건 모두에서 공통적으로 강화 입자의 분포가 용융풀의 외곽 부분에 상대적으로 밀집되어 있는 것을 확인 할 수 있다. 이는 용융풀 내 유동에 의한 현상으로 확인된다. Fig. 6(c)를 보면 용융풀 내의 유동은 기판(substrate) 면을 기준으로 용융풀의 중앙에서 전면으로 흐른 뒤, 외곽으로 회전하는 양상을 보인다(주황 선). 이 때 용융풀 중앙부 온도 대비 낮은 온도 분포를 보이는 최외곽에서 용융 금속의 점성이 높아 해당 부위에서 높은 저항을 가지게 되는데, 이로 인해 최외곽에서는 유속이 매우 감소하고 강화 입자의 밀도가 외곽에서 높은 수치를 보인다고 할 수 있다.

본 연구에서는 강화 나노 입자가 포함된 에너지 직접 용착 공정 상 용융풀 거동을 모델링하고, 그에 따른 나노 입자의 분포를 추적하는 이상유동모델 해석방법을 제시하였다. 용융풀의 정확한 예측을 위해 에너지 직접 용착 공정 중 발생하는 다양한 물리현상(Multiple reflection of laser ray, recoil pressure, phase change 등)을 고려하였다. 제시된 모델을 통한 용융풀 해석 결과 용융풀 단면의 Width, Height, Dilution의 예측 값이 실험결과 대비 평균적으로 10% 내외 수준의 예측 정확도를 보임을 확인하였으며, 에너지 직접 용착 공정 중 발생하는 용융풀 내부의 유동 흐름을 확인하고 분석하였다.
이러한 용융풀 내부의 열적 거동 및 유동 흐름 해석 데이터를 기반으로 이상유동모델 기법을 활용하여 파우더 내 포함된 강화입자(본 연구에서는 TiC 사용)의 용융풀 내 분산을 예측하였다. 입자의 크기를 고려하여 항력, 양력, 부력과 더불어 브라운력 및 열영동력이 포함된 지배 방정식에 따라 거동을 더욱 엄밀히 예측하였다. 거동 분석 결과 공정 조건에 따라 강화 입자의 분포가 달라짐을 확인할 수 있었으며 용융풀 내부의 유동흐름에 의해 용융풀 최외곽에 입자의 분포밀도가 높아짐을 확인하였다.
본 연구에서 제시하는 해석모델을 통해 용융금속의 결정화과정에서 결정핵(crystal nucleus) 역할을 수행하는 나노 크기의 강화입자가 용융풀 내부에서 어떤 거동을 보이는지 확인할 수 있으며, 이를 기반으로 입자의 최종 분포를 예측할 수 있다. 향후에는 에너지 직접 용착 공정에서 만들어지는 제조물 물성의 보다 정확한 예측을 위해 이상유동모델 기반 입자분포 예측모델을 결정성장 모델과 병합하여 강화입자가 포함된 에너지 직접 용착 공정에서의 제조물의 미세구조를 예측하는 멀티스케일 해석 기법의 연구가 가능할 것으로 판단된다. 또한 본 연구는 제한된 공정변수 조합에 대해서만 해석을 진행하였다는 한계점이 존재하기 때문에, 향후 연구에서는 공정 변수 범위를 확대하여 공정변수에 따라 달라지는 용융풀 거동을 확인하고, 그에 따른 강화입자의 분포 예측 지도를 도출함으로써 제시된 해석모델의 활용성을 넓힐 수 있을 것으로 사료된다.

이 논문은 2024년도 정부(방위사업청)의 재원으로 국방기술진흥연구소의 지원을 받아 수행된 연구임(No. 21-106-A00-006(KRIT-CT-23-019), 반응성 고증착률 적층제조 기술 특화연구실).