- Finite Element Analysis of Stress Responses in Biaxial Specimen Geometries
Yoonsub Woo*, Hyungbum Park*†
*Department of Mechanical Engineering, Incheon National University
- 유한요소해석 기반 이축변형시편 형상에 따른 응력 거동 평가
우윤섭* · 박형범*†
This article is an open access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
This study aims to evaluate the suitability of various geometrical shapes of biaxial deformation specimens for assessing the biaxial deformation behavior of polymer materials through finite element analysis. The research comprehensively considered various geometries presented in the literature to determine the optimal specimen shape that ensures stress concentration in the gauge section, reduces shear stress, and promotes failure through high plastic deformation in the gauge section. To assess suitability, the average stress in the gauge section and the maximum stress in the notch section during biaxial tensile deformation were quantitatively derived and comparatively analyzed. First, analyzing the stresses in the gauge and notch sections for circular gauge sections with varying curvatures showed that a large curvature in the notch section significantly concentrated stress there, but the benefit to the gauge section stress was minimal. In contrast, an indented notch shape significantly increased stress in the gauge section while substantially alleviating stress concentration in the notch section compared to notches with large curvatures. Regarding the influence of gauge section geometry, it was confirmed that modifying the gauge section to a rhombus shape could alleviate stress in the notch section. Although this alleviation effect was minimal for low-curvature notches, indented notches showed a stress reduction effect of over 5 MPa. These findings are expected to serve as fundamental data for designing biaxial deformation specimens for polymer materials, a topic that has not yet been clearly established.
본 연구는 고분자 재료의 이축 변형 거동을 평가하기 위한 이축 변형 시편의 다양한 기하학적 형상을 고려하여, 이축 주응력 측정의 적합성을 유한요소해석을 통해 평가하고자 한다. 본 연구에서는 이축 변형 시편 설계 시 목표로 하는 게이지 부의 응력 집중 및 전단 응력의 저감과, 높은 소성 변형 유도를 통한 게이지 부 파괴 유도를 위해 기존 문헌에 제시된 다양한 형상을 종합적으로 고려하여 시편 형상의 적합성을 조사하였다. 적합성을 판단하기 위하여, 이축 인장 변형 상에서 게이지 부에서의 평균 응력과 노치부에서의 최대 응력을 정량적으로 도출하여 비교 분석하였다. 우선 가장 많이 활용되는 원형 형태의 게이지부에서 서로 다른 곡률에 따른 게이지 및 노치 부 응력을 분석한 결과, 노치부의 큰 곡률은 노치부 응력을 크게 집중시키지만 게이지 부의 응력에서의 이득은 그리 크지 않은 것으로 조사되었다. 반면에 함몰형 노치부는 게이지 부의 응력을 크게 증가시키며, 큰 곡률을 지닌 노치 부와 비교하였을 시 노치 부 응력 집중을 대폭 완화시키는 것으로 확인되었다. 게이지 부의 형상에 따른 조사 결과로는, 게이지 부 형상의 마름모꼴 변경이 노치 부의 응력을 완화시킬 수 있음이 확인되었다. 낮은 곡률의 경우에 이러한 완화 효과는 미미하지만, 함몰형 노치부의 경우 5MPa 이상의 응력 완화 효과를 나타냄을 확인하였다. 해당 연구 결과는 현재까지 정립되지 않은 고분자 소재의 이축변형시편의 형상을 설계함에 있어서 기초 자료로 활용될 수 있을 것으로 기대한다.
Keywords: 이축변형시험(Biaxial deformation tests), 이축변형시편(Cruciform specimens), 유한요소해석(Finite element analysis), 고분자소재(Polymers), 소성변형(Plastic deformations)
일반적으로, 부품의 기계적 수명을 정확히 평가하고, 보다 진보된 설계를 위해서는, 구성 소재의 3차원 응력 거동을[1,2] 정밀히 규명하는 것이 요구된다. 단순하게 단축 하중 상황에서 측정한 항복 및 파괴 응력의 기준만으로는 하중 상황이 다축으로 변화됨에 따라 해당 기준이 더 이상 유효하지 않을 수 있다[3]. 따라서, 소재의 정밀한 3차원 항복 및 파괴 기준을 확립하는 것은 매우 중요하며, 이축, 삼축 하중 조건에서의 변형 거동 평가 방법론이 이를 위해 활용된다. 일반적으로 이축변형시편, 튜브형 시편, Arcan 시편 등을 활용한 다양한 다축 변형 시험 방법론이 존재하며, 요구되는 하중 방향 및 소재 특성에 따라 알맞게 적용된다. 그러나, 표준화가 완료된 보편적인 3차원 응력 측정 시험법은 부재한 상황이며, 다양한 시험기기 및 방법론이 여전히 개발되어지고 있다.
십자 형태의 시편을 활용하는 이축 변형 시험(Cruciform test)은 재료의 다축 변형 거동을 평가하는 대표적인 방법 중 하나로, 두 축 방향으로 동시에 하중을 부과하여, 다축 기계적 변형 거동을 정밀히 분석할 수 있다. 이와 같은 변형 시험 시, 시편의 형상은 시험의 정확성과 결과 신뢰성에 영향을 미치는 핵심 변수이다. 기존 대부분의 연구는 금속 소재의 이축 변형 시험을 위한 이축 변형 시편의 형상 확립에 초점을 맞추어 진행되었다. 바람직한 시편의 형상은 게이지 부에서 높은 응력 집중을 유도해 파손이 발생하도록 설계하는 동시에, 게이지 부 내에서 높은 소성 변형을 유도할 수 있어야 한다. 이 과정에서, 게이지 부 내에서 의도하지 않은 전단 응력 및 변형률은 최소화되어야 한다. 이를 위해 게이지 부의 두께를 얇게 설정하고[4-6], 시편의 팔 부분에 슬릿 형상을 추가하여 게이지 부로 유도되는 하중이 직접적으로 전달되도록 형상을 고안하였다. 또한, 시편의 팔이 서로 맞닿는 모서리 영역인 노치 부의 형상을 다양하게 설계하여, 노치 부에서 발생하는 응력 집중을 최소화하는 방법 또한 제시되었다[7-10]. 이러한 연구의 결과로 금속 소재의 복잡한 변형 거동을 정밀하게 평가할 수 있는 최적화된 시편 설계가 완성되었으며[11,12], 이는 국제 표준화 기구인 ISO에 공식적으로 등록된 상황이다.
그러나 해당 표준화 시편 형상을 복합소재용 고분자 소재에 직접적으로 적용하기에는 매우 제한적이다[13,14]. 표준화된 시편 형상은 균일한 하중을 게이지 부에 전단의 영향을 최소화하여 전달하기 위해 얇은 슬릿 구조를 도입하였는데, 슬릿 구조는 높은 취성을 지니는 고분자 소재에는 시편 파단 문제로 인하여 도입이 어렵다는 단점이 존재한다[15-18]. 또한 표준 시편 형상은 높은 소성 변형률을 게이지 부에 발생시킬 수 없다는 단점이 존재하기에, 항복 이후의 항복 표면의 진전을 효과적으로 도출하기가 어렵다는 한계점이 존재한다. 따라서, 에폭시와 같은 취성 고분자 소재를 활용한 이축 변형 시험에서는 금속 소재의 시편 설계를 그대로 적용하기보다, 고분자 소재의 특성을 고려한 맞춤형 설계가 요구되는 실정이다[19,20].
본 연구에서는 게이지 부의 얇은 두께와 슬릿 형상을 통한 응력 집중 유도 방식을 배제하고, 십자형 시편의 성능을 결정짓는 주요 요소인 게이지 부와 노치 부의 구조적 변수들이 응력 분포와 변형 거동에 미치는 영향을 유한요소해석을 활용하여 종합적으로 분석하고자 한다. 특히, 본 연구에서는 게이지 부와 노치 부 사이의 응력 집중 정량 분석을 통하여, 구조적 형상이 게이지 외부 소성변형 및 파단에 미치는 영향성을 검토하고자 한다.
2.1 주요 구조 변수
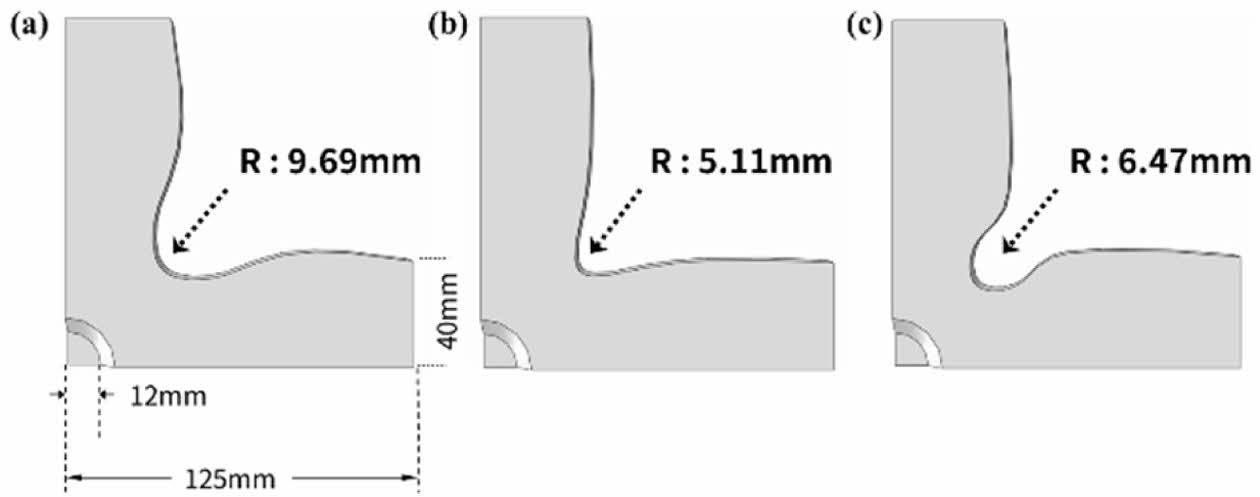
이축 변형 시편의 노치 부의 형상은 시편의 전체적인 응력 분포에 결정적인 영향을 미치는 핵심 구조적 변수이다. 노치 부의 형상은 게이지 부에서의 응력 분포 및 첫 소성 변형이 발생하는 위치에 지대한 영향을 미치며, 동시에 노치 부의 응력 집중 정도를 결정 짓는다. 본 연구에서는 게이지 부 형상을 원형으로 고정시키고 노치 부의 형상을 곡률에 따라 낮은 곡률형(1), 높은 곡률형(2), 함몰형(3)으로 분류하고 해석 결과를 비교하고자 한다[19,21]. 각 곡률 별 1/4 시편 형상을 Fig. 1에 아래와 같이 나타내었다.
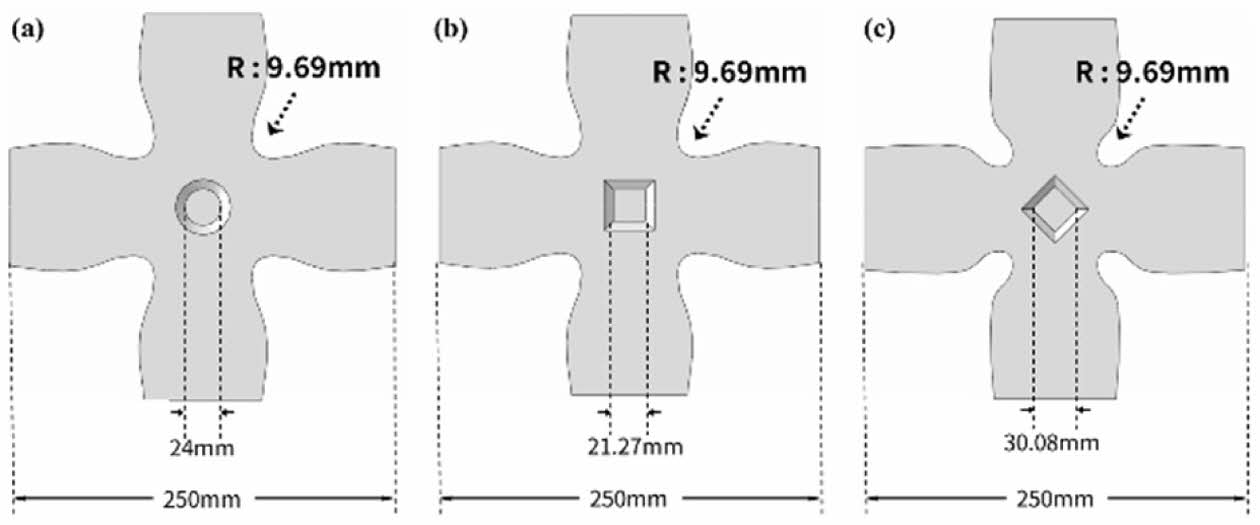
또한, 다양한 게이지 부 형상에 따라 게이지 부 및 노치 부 응력 분포에 대해서도 조사하였다. 기존 문헌에서 제안된 여러 게이지 부 형상을 기반으로[14], 원형, 사각형, 마름모형의 세 가지 형상을 대표 사례로 선정하여 비교 분석 하였다. 각 시편 형상과 구체적 치수는 Fig. 2에 제시되어 있다.
모든 시편 형상들은 게이지 부 가장자리에서의 응력 집중을 완화하고자 시편의 끝 부분 두께로부터 점진적으로 얇아지게끔 구성되었으며, 이때의 테이퍼링 각도는 45°로 설정하였다. 제안된 시편 모델들의 세부 형상 치수는 기존 연구에서 제안된 시편 형상들을 수집하여 형상의 특성을 가장 잘 반영할 수 있도록 결정되었다[22-24].
2.2 유한요소해석 방법론
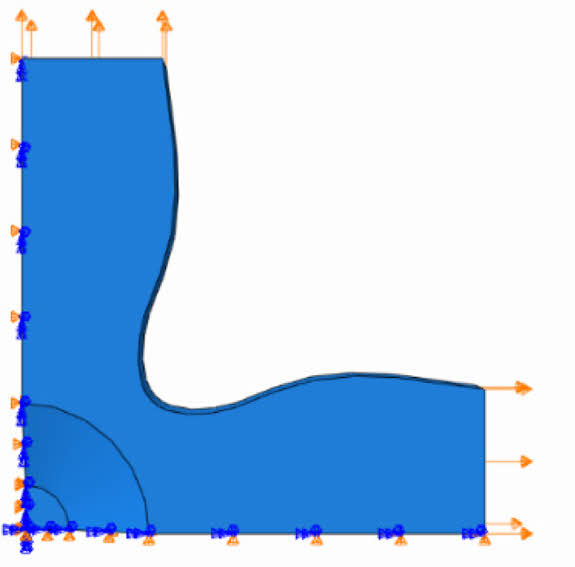
등이축 인장 변형 시 응력 거동을 조사하기 위하여 유한요소해석을 수행하였다. 경계 조건은 시편의 팔(arm) 부에 변위를 부여하였으며, 충분한 소성 변형을 관찰하기 위해 최대 변형률이 약 8%에 도달하는 1 mm의 변위를 설정하였다. 또한, 계산 효율성을 제고하기 위해 모델은 4분할 되어 구축하였고, 분할 대칭단면에는 XSYMM 및 YSYMM 경계조건을 부여하여 실제 시편의 대칭적 거동을 재현하였다(Fig. 3).
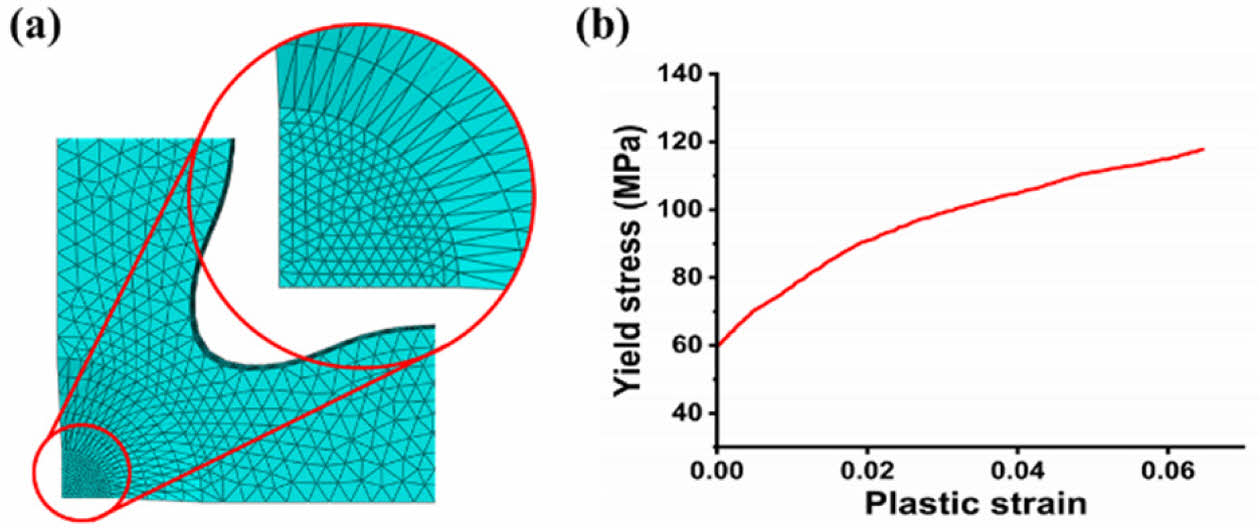
특히, 응력이 집중되는 게이지 부의 거동을 정밀하게 분석하기 위해 해당 영역의 메쉬 크기를 1 mm로 설정하여 (팔 부의 약 1/5) 해석의 정밀성을 높였다(Fig. 4(a)). 아울러, 시뮬레이션에 사용된 물성치로는 실험적으로 측정된 에폭시 수지의 기계적 물성을 활용하였다[25]. 이때, 해당 에폭시 소재는 게이지 및 노치부의 응력 집중에 따른 변형을 명확히 이해하고자, 충분한 연성 특성을 나타내는 소재로 선정되었다. 구성방정식으로 탄성 영역은 3차원 훅의 법칙으로, 소성 영역은 3차원 von-Mises 항복 기준을 활용하였다. 이때 탄성 계수 및 프아송 비는 각각 2980.21 MPa, 0.4의 값으로, 항복 응력은 59.72 MPa로 설정되었다. 항복 이후 거동은 Fig. 4(b)에 도시되었다.
2.3 응력 분석
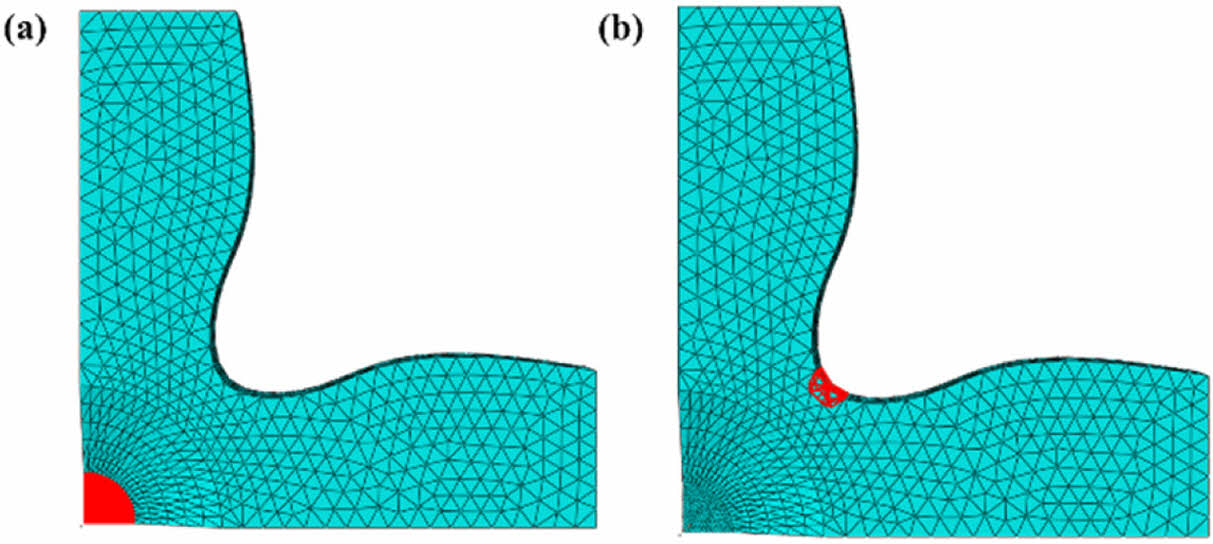
시뮬레이션 결과를 분석하기 위한 주요 지표로는 1) 게이지 부 내의 평균 응력, 2) 노치 부 내의 최대 응력, 3) 최초 소성 변형 발생 위치, 4) 게이지 부 내에서의 최대 전단 응력을 선정하였다. 이러한 지표들은 각 형상의 특성을 체계적으로 분류하는 데 활용되며, 이를 토대로 보다 적합한 형상을 도출할 수 있는 근거를 제공한다. 게이지 부와 노치 부의 영역의 예시는 Fig. 5에 도시되어 있다. 게이지 부는 두께가 3 mm로 설정된 영역의 모든 요소들로, 노치부는 모델의 y=x 대칭 축 상에서의 모델 내 끝 부분을 기점으로 반지름 5 mm 내에 속한 요소들로 상정되었다.
게이지 부의 응력은 식 (1)에서 볼 수 있듯, 영역 내에 있는 요소의 부피가 각각 다름을 반영하여 각 요소의 von-Mises 등가 응력과 부피를 곱한 값을 모두 더한 후, 영역의 전체 부피로 나누는 부피 평균 값을 활용하였다. 반면, 노치 부의 응력은 단순한 평균값 계산 대신 최대 응력을 근사하기 위한 p-norm 응력을 적용하여 산출하였다. 식 (2)에 제시된 p-norm 응력은 특정 영역내의 응력 값을 최대값으로 근사화 할 수 있는 방식으로 p값이 커짐에 따라 최대응력에 근사된다[26]. p 값에 따른 최대 응력 값의 민감도를 고려하여, 경험적으로 결정된 값인 20를 가중치 p로 설정하였다. 마지막 응력 분석 지표로, 시편 형상이 게이지 부 내 전단 응력 발생에 미치는 영향을 관찰하고 이를 분석하기 위해 게이지 부 내에서 발생하는 평균 전단 응력을 계산하였다. 게이지 부 내의 요소에서 발생하는 τxy, τyz, τzx의 전단 응력 값들 중 최대 전단 응력을 활용하여 비교 분석하였다.
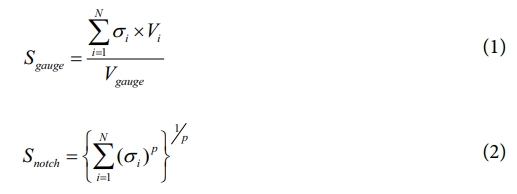
|
Fig. 1 Three different notch section geometries: (a) low curvature, (b) high curvature, and (c) indented geometry |
|
Fig. 2 Three different gauge section geometries: (a) Circular, (b) Square, and (c) Rhombus |
|
Fig. 3 Boundary conditions and load direction for the quartered specimen |
|
Fig. 4 (a) Fine mesh size in the gauge section for accurate stress distribution analysis, and (b) Yield stress as a function of plastic strain for epoxy resin |
|
Fig. 5 Highlighted region: (a) gauge section, (b) notch section |
3.1 노치 부 형상 비교
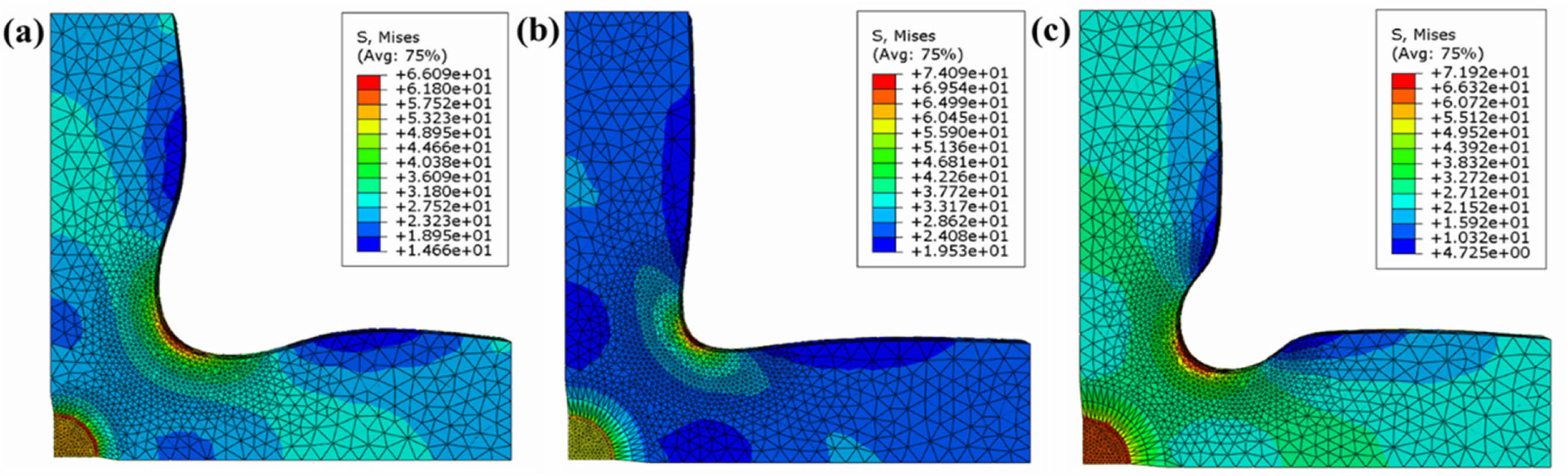
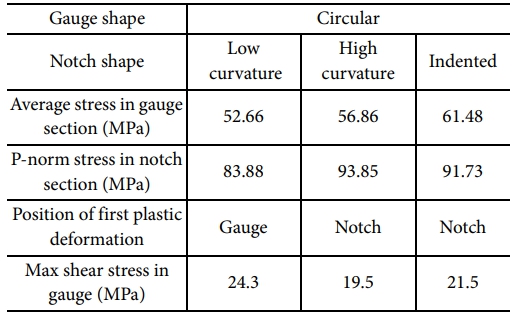
앞서 설명한 세 가지 노치 부 곡률을 적용한 모델을 활용하여 유한요소해석을 수행하고, 제안된 네 가지 결과 지표를 계산하여 형상을 비교하였다. 각 시편의 해석 결과는 (마지막 인가 변위 시점 기준) Fig. 6에 제시하였으며, 네 가지 주요 결과 지표는 Table 1에 정리하였다. 모든 시편에서 게이지 부의 응력 집중이 발생하였으며, 곡률의 정도에 따른 기계적 거동의 차이를 확인할 수 있었다.
우선 게이지 부의 응력을 비교할 시, 낮은 곡률, 높은 곡률, 함몰형 시편의 순서대로 평균 응력 값이 증가함을 알 수 있다. 이때 단순 곡률의 증가는 게이지 부 응력 값을 효과적으로 증가시키지 못함을 확인하였다. 반면에 함몰형의 경우, 노치부 소재 영역 감소로 인하여 게이지 부에 높은 응력을 인가할 수 있다는 점이 확인되었다.
노치 부의 응력을 비교하였을 시, 높은 곡률의 형성은 낮은 곡률 대비 약 10 MPa의 높은 노치 부 응력 집중을 야기함을 확인하였다. 따라서, 단순 곡률을 증가시키는 것은 게이지 부의 응력을 효과적으로 상승시키지 못함과 동시에 노치부의 응력 집중을 배가하는 것으로 확인되었다. 이러한 관점에서 함몰형 노치 부의 형태는 높은 곡률 결과 대비 노치 부 응력을 약 2 MPa 정도 낮출 수 있음을 확인하였다. 이는 적절한 노치 부 함몰을 통해 게이지 부와 노치 부의 응력 커플링을 완화할 수 있음을 나타낸다.
소성 변형의 시작 위치 조사 결과, 낮은 곡률 모델만 게이지 안쪽에서 소성 변형이 시작됨을 알 수 있다. 따라서 함몰형 시편의 경우에는 노치 부와 게이지 부 간의 응력 밴드를 완화하지 못할 시, 시편의 파단은 게이지 외곽에서 시작될 수 있음을 알 수 있다. 전단 응력의 경우는 세 시편 형상 모두 적지 않은 값(10 MPa 이상)을 나타내었기에, 이에 대한 영향을 축소시킬 수 있는 방안이 필요함을 확인하였다.
3.2 게이지 부 형상 비교
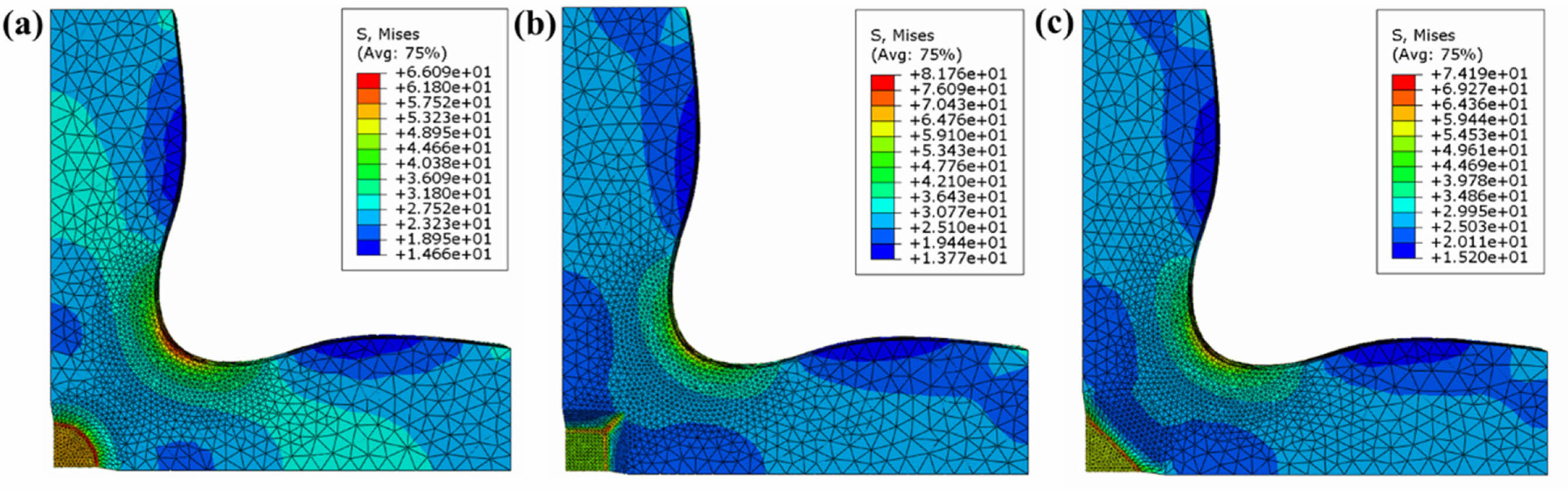
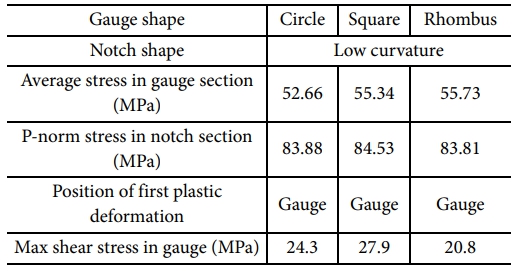
제안된 세 가지 게이지 부 형상인 원형, 사각형, 마름모형 모델에 대해 유한요소해석을 수행하여 각 형상의 기하학적 특징이 시편의 응력 분포에 미치는 영향을 분석하였다. 앞선 Table 1의 결과에 따르면, 낮은 곡률형 노치 부 형상이 가장 낮은 노치 부 응력을 가지며, 첫 소성 변형이 유일하게 게이지 부에서 발생하여 세 가지 형상 중 시편 목적에 가장 적합한 것으로 평가되었다. 이에 따라, 게이지 부 형상 분석에서 기본 노치 부 형상으로 낮은 곡률형 노치 부를 채택하였다. 게이지 부 형상에 따른 해석 결과는 Fig. 7에 도시되어 있으며, Table 2에 네 가지 주요 지표가 정리되어 있다.
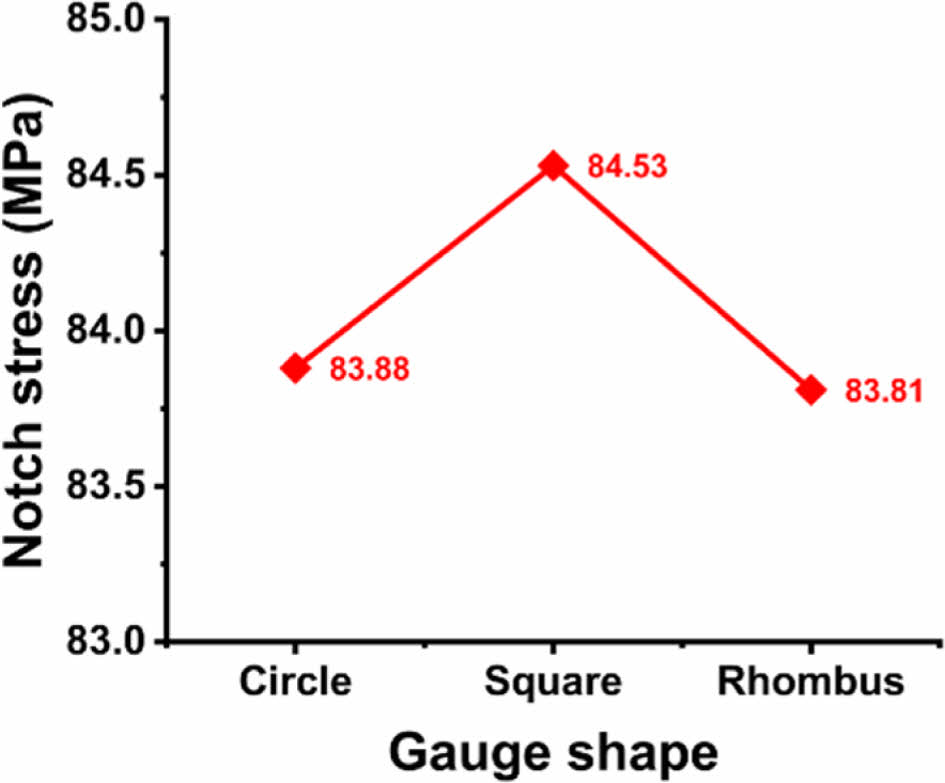
Table 2의 계산된 지표 값을 비교하면, 다른 형상의 게이지 부에 비해 마름모형 게이지 부가 더 낮은 노치 부 응력을 가지는 것을 확인할 수 있다. 이는 마름모형 게이지 부가 이축 인장 시뮬레이션 중 노치 부로 전파되는 응력 분포를 하중 방향인 시편의 팔 방향으로 응력을 집중적으로 전환하는 것으로부터 기인한다. 반면, 사각형 게이지 부는 응력 분포를 노치 부로 더 강하게 집중시키는 특징을 가지므로, 마름모형 게이지 부보다 더 높은 노치 부 응력이 발생하는 것을 확인할 수 있다(Fig. 8). 그러나 이러한 영향은 Table 1에서 제시된 노치부의 형상에 따른 영향보다는 매우 미미한 값임을 확인할 수 있다. 다른 주요 지표 중 하나인 노치 부 내 최대 전단 응력 값은 마름모형 게이지 부에서 가장 낮은 수치를 기록하였으며, 이는 게이지 부의 빗면이 하중 방향과 이루는 각도에 따라 전단 응력의 수준이 달라지기 때문으로 해석된다. 아울러, 게이지 부 응력과 첫 소성 변형의 위치는 세 가지 시편에서 모두 유사한 결과를 보였으며, 이는 게이지 부 응력이 노치 부의 형상 변화보다 게이지 부 형상 변화에 둔감하게 반응한다는 점을 시사한다. 결론적으로, 노치 부 응력이 가장 낮고 게이지 부에서 발생하는 전단 응력을 효과적으로 방지할 수 있는 마름모형 시편이 게이지 부 형상 중 가장 적합한 것으로 판단된다.
3.3 종합 비교
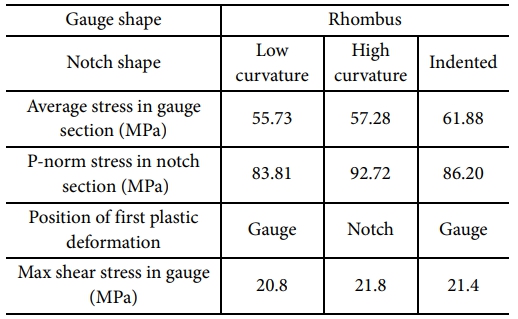
앞선 결과에 따르면, 마름모형 게이지 부는 이축 인장 시뮬레이션 중 노치 부로 전파되는 응력 분포를 하중 방향인 시편의 팔 방향으로 유도할 수 있는 특성을 지니는 것으로 확인하였다. 이러한 결과를 기반으로 정의된 3가지 노치 부 형상 모델을 마름모형 게이지 부 조건에서 구축하여 유한요소해석을 수행하고 결과를 비교 분석하였다. 마름모형 게이지 부를 적용한 시편의 형상과 해석 결과는 Fig. 9와 10에 도시되어 있으며, 각 형상에서 계산된 네 가지 결과 지표는 Table 3에 정리하였다.
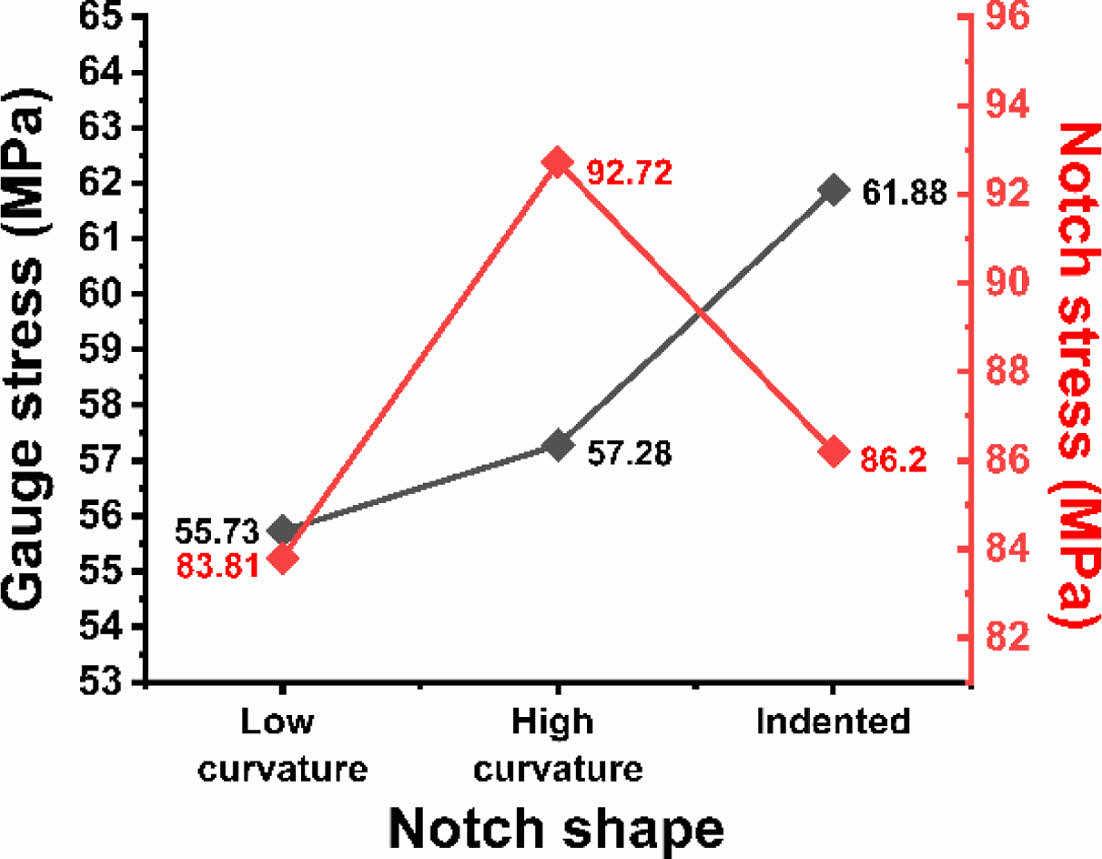
Table 3의 계산된 결과 지표에 따르면, 함몰형 노치 부를 가진 시편은 다른 시편에 비해 약 4-6 MPa 높은 게이지 부 응력을 가지면서도 상대적으로 낮은 노치 부 응력을 보인다. 이를 앞선 원형 게이지 부 해석 결과(Table 1)와 비교하면, 게이지 부를 마름모형으로 변경함으로써 원형 게이지 부와 함몰형 노치 부를 가진 시편의 주요 단점이었던 높은 노치 부 응력이 완화되었음을 확인할 수 있다(Fig. 11 참고). 함몰형 노치 부를 가진 시편에서 게이지 부의 최대 전단 응력은 다른 시편에 비해 약 1 MPa 정도 높게 나타나지만, 전반적으로 최대 전단 응력은 원형 게이지 부 결과들에 비해 낮음을 알 수 있다. 소성 변형의 위치 또한 게이지 내부에서 발생하여 시편 설계 방향에 부합함을 알 수 있다.
이와 같은 결과가 시사하는 바는 이축 변형 시편에서의 고질적인 문제점인 게이지 및 노치 부의 응력 커플링 현상을 게이지 부의 형상과 노치부 곡률, 함몰 정도에 따라 적절하게 조절할 수 있다는 점이다. 특히, 게이지 부의 형상의 선정에 따라 이러한 게이지 및 노치 부의 응력 커플링의 정도를 조절할 수 있음을 확인하였다. 마름모 꼴의 게이지 부를 선정 시, 함몰 형의 노치부를 모델링하더라도 원형 게이지 부 결과와 대비하여 노치 부 응력 차이를 5 MPa 정도 축소시킬 수 있다. 또한, 추가적으로 최적화 과정을 통하여 노치 부 곡률과 함몰 정도에 따라서 노치부의 응력 집중을 저감시킬 수 있는 최적화의 가능성 또한 존재함을 시사한다.
|
Fig. 6 Results of biaxial tension tests based on FEM simulations for different notch section shapes: (a) Low curvature, (b) High curvature, and (c) indented shapes |
|
Fig. 7 Results of biaxial tension test according to gauge section shape based on FEM simulations: (a) Circular, (b) Square, (c) Rhombus shapes |
|
Fig. 8 Graph comparing notch section stresses based on different gauge section shapes |
|
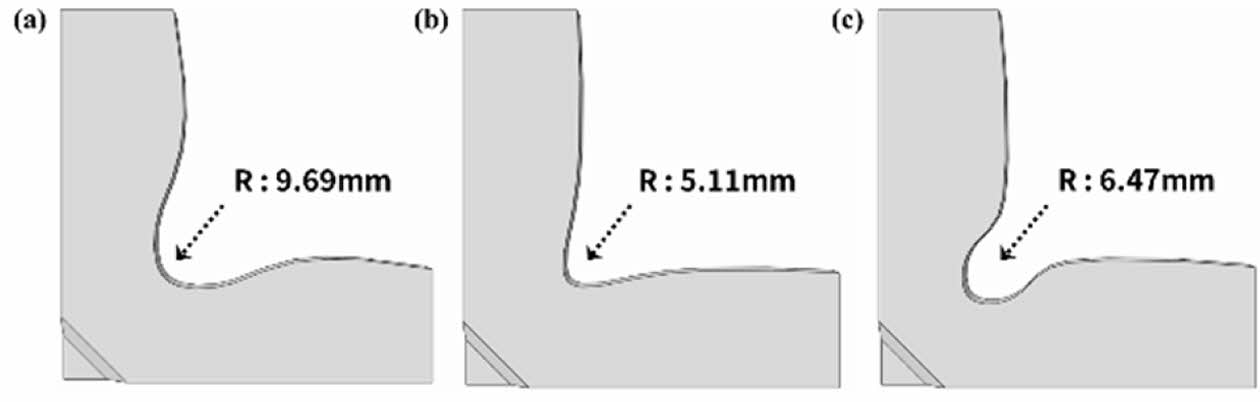
Fig. 9 Three notch geometries based on rhombus gauge section: (a) low curvature, (b) high curvature, (c) indented shapes |
|
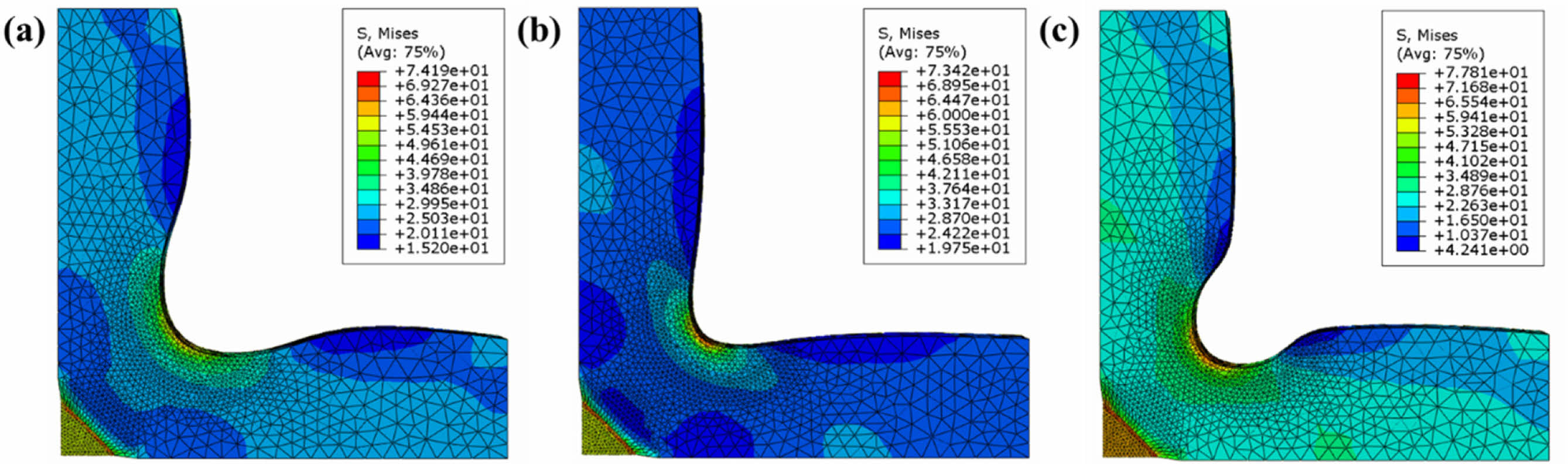
Fig. 10 Results of biaxial tension test according to notch section shape based on FEM simulations with rhombus gauge section: (a) low curvature, (b) high curvature, (c) indented shapes |
|
Fig. 11 Comparison of gauge section and notch section stresses of rhombus-shaped gauge specimens |
|
Table 1 Calculated indicators through FEA of three notch sections based on a circular gauge section |
|
Table 3 Calculated result indicators of three notch shapes based on a rhombus gauge section |
본 연구에서는 이축 변형 시편 형상 분석을 목표로 유한요소해석을 활용하여 각 형상의 기하학적 특성이 시편의 응력 분포와 소성 변형 거동에 미치는 영향을 평가하였다. 노치 부의 세 가지 형상을 비교한 결과, 노치 부의 함몰 정도 및 곡률 값의 선정에 따라 게이지 부의 응력 집중 정도가 달라짐을 확인하였다. 그러나, 동시에 게이지 부 및 노치 부의 응력 커플링 현상으로 인해, 게이지 부의 응력 유도는 노치 부의 응력 또한 집중시킴을 확인하였다.
게이지 부의 형상 해석 결과로는, 제안된 게이지 부의 형상 중, 마름모형 게이지 부가 노치 부의 응력 집중을 효과적으로 완화함을 확인하였다. 특히, 함몰형 노치 부와 마름모형 게이지 부가 결합한 시편 형상은 게이지 부로의 응력 전달을 유지하면서도 노치부 응력을 효과적으로 완화함을 확인하였다. 본 결과는 향후 게이지 부의 형상, 노치부의 곡률 및 함몰 정도의 적절한 조합이 이축 변형 시편 형상의 설계에 필요함을 시사한다.
본 연구는 2025, 국가과학기술연구회, CRC23012-000, 재활용 가능한 미래 에어모빌리티 구조용 소재 부품 경량화 플랫폼 기술 개발, 2023.07.01 – 2029.06.30 사업과 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. 2022R1F1A1073774)을 밝힙니다.
- 1. Kim, J.Y., and Park, H.B., “Evaluation of Yield Surfaces of Epoxy Polymers Considering the Influence of Crosslinking Ratio: A Molecular Dynamics Study,” Composites Research, Vol. 36, No. 5, 2023, pp. 369-376.
-

- 2. Chang, S.-H., “Microscopic Observation of Draped Composite Materials : Bias Extension and Biaxial Tests,” Composites Research, Vol. 17, No. 1, 2004, pp. 38-46.
- 3. Meng, Y., et al., “Identification of True Stress-strain Curve of Thermoplastic Polymers Under Biaxial Tension,” SAE International Journal of Materials and Manufacturing, Vol. 9, No. 3, 2016, pp. 768-775.
-

- 4. Creuziger, A., et al., “Insights into Cruciform Sample Design,” JOM, Vol. 69, No. 5, 2017, pp. 902-906.
-

- 5. Lamkanfi, E., et al., “Strain Distribution in Cruciform Specimens Subjected to Biaxial Loading Conditions. Part 2: Influence of Geometrical Discontinuities,” Polymer Testing, Vol. 29, No. 1, 2010, pp. 132-138.
-

- 6. Lu, Z., et al., “Optimization Design of a Small-Sized Cruciform Specimen for Biaxial Fatigue Testing,” Metals, Vol. 10, No. 9, 2020, pp. 1148.
-

- 7. Baptista, R., et al., “Optimization of Cruciform Specimens for Biaxial Fatigue Loading with Direct Multi Search,” Theoretical and Applied Fracture Mechanics, Vol. 80, 2015, pp. 65-72.
-

- 8. Makris, A., et al., “Shape Optimisation of a Biaxially Loaded Cruciform Specimen,” Polymer Testing, Vol. 29, No. 2, 2010, pp. 216-223.
-

- 9. Zhao, K., et al., “Design of a Biaxial Tensile Testing Device and Cruciform Specimens for Large Plastic Deformation in the Central Zone,” Journal of Materials Science, Vol. 54, No. 9, 2019, pp. 7231-7245.
-

- 10. Correa, E., et al., “Design for a Cruciform Coupon Used for Tensile Biaxial Transverse Tests on Composite Materials,” Composites Science and Technology, Vol. 145, 2017, pp. 138-148.
-

- 11. Upadhyay, M.V., et al., “Stresses and Strains in Cruciform Samples Deformed in Tension,” Exp Mech, Vol. 57, No. 6, 2017, pp. 905-920.
-

- 12. Zhu, Z., et al., “Optimal Design of a Miniaturized Cruciform Specimen for Biaxial Testing of TA2 Alloys,” Metals, Vol. 9, No. 8, 2019, pp. 823.
-

- 13. Park, H., et al., “Characterizing the Biaxial Compressive Deformation Behavior of epoxy Polymer Through Cruciform Experiment and Finite Element Analysis,” Composite Structures, Vol. 305, 2023, pp. 116488.
-

- 14. Horta Munoz, S. and Serna Moreno, M.D.C., “Advances in Cruciform Biaxial Testing of Fibre-Reinforced Polymers,” Polymers (Basel), Vol. 14, No. 4, 2022, pp. 686.
-

- 15. Park, S.-M., et al., “Numerical Investigation of the Progressive Failure Behavior of the Composite Dovetail Specimens under a Tensile Load,” Composites Research, Vol. 34, No. 6, 2021, pp. 337-344.
-

- 16. Smits, A., et al., “Design of a Cruciform Specimen for Biaxial Testing Of Fibre Reinforced Composite Laminates,” Composites Science and Technology, Vol. 66, No. 7-8, 2006, pp. 964-975.
-

- 17. Tang, J., et al., “Failure Analysis of Plain Woven Glass/epoxy Laminates: Comparison of Off-axis And Biaxial Tension Loadings,” Polymer Testing, Vol. 60, 2017, pp. 307-320.
-

- 18. Lang, J., et al., “Investigations of Cruciform Specimen Designs for Biaxial Tensile Testing of SMC,” in Proceedings. MDPI, 2018.
-

- 19. Lamkanfi, E., Van Paepegem, W., and Degrieck, J., “Shape Optimization of a Cruciform Geometry for Biaxial Testing of Polymers,” Polymer Testing, Vol. 41, 2015, pp. 7-16.
-

- 20. Kobeissi, A., et al., “Strength Characterization of Glass/epoxy Plain Weave Composite under Different Biaxial Loading Ratios,” Journal of Composite Materials, Vol. 54, No. 19, 2020, pp. 2549-2563.
-

- 21. Moncy, A., et al., “Understanding the Effect of Anisotropy in Composite Materials on the Performance of Cruciform Specimens,” Composite Structures, Vol. 273, 2021, pp. 114225.
-

- 22. Youssef, Y., et al., “Specimen Design, Manufacturing and Testing Procedures for Flat Carbon Fiber Reinforced Plastic Laminates under Biaxial Loading,” Polymer Composites, Vol. 19, No. 3, 1998, pp. 257-263.
-

- 23. Escárpita, D.A.A., et al., “Biaxial Tensile Strength Characterization of Textile Composite Materials,” in Composites and Their Properties, IntechOpen, 2012.
-

- 24. Xu, C., et al., “Experimental Investigation on the Mechanical Behaviour of 3D Carbon/carbon Composites under Biaxial Compression,” Composite Structures, Vol. 188, 2018, pp. 7-14.
-

- 25. Ma, X., et al., “Synthesis and Mechanical Properties of the Epoxy Resin Composites Filled with Sol-gel Derived ZrO2 Nanoparticles,” Journal of Sol-Gel Science and Technology, Vol. 88, 2018, pp. 442-453.
-

- 26. Le, C., et al., “Stress-based Topology Optimization for Continua,” Structural and Multidisciplinary Optimization, Vol. 41, 2010, pp. 605-620.
-

 This Article
This Article
-
2025; 38(2): 132-138
Published on Apr 30, 2025
- 10.7234/composres.2025.38.2.132
- Received on Jan 20, 2025
- Revised on Feb 11, 2025
- Accepted on Mar 17, 2025
 Services
Services
Shared
 Correspondence to
Correspondence to
- Hyungbum Park
-
Department of Mechanical Engineering, Incheon National University
- E-mail: gamamle@inu.ac.kr






 Copyright ⓒ The Korean Society for Composite Materials. All rights reserved.
Copyright ⓒ The Korean Society for Composite Materials. All rights reserved.