This study analyzes the restraining force of the hang-off clamp and the safety of the wire during submarine cable installation using the Flexible Pull-in Installation System (FPIS). In particular, for permanent clamps, it is crucial to examine the potential for slip and failure due to self-weight before and during installation, as well as additional loads after fastening. To achieve this, numerical analysis was conducted to evaluate the maximum frictional resistance of the clamp and the possibility of wire damage. The analysis results indicate that the minimum frictional load generated in the temporary clamp is approximately 34.63 kN, which is about 14% higher than the target weight of 30 kN for the cable and protective equipment. Additionally, when the permanent clamp is fastened, the maximum stress observed in the clamp is 414.4 MPa, while the maximum stress in the wire reaches 881.3 MPa. Although the wire's maximum stress exceeded the material’s tensile strength, this was attributed to localized stress concentration. Buckling and deformation were observed; however, the possibility of complete failure was determined to be low.

본 연구에서는 유연 입상 설치 시스템(Flexible Pull-in Installation System, FPIS)에서 해저 케이블 설치 시 하중을 지지하는 행오프 클램프(Hang-off Clamp)의 구속력과 와이어의 안전성을 분석하였다. 특히, 영구 클램프(Permanent clamp)의 경우 케이블 설치 전과 체결 전의 자중, 그리고 체결 후 추가 하중에 따른 슬립 및 파단 여부를 면밀히 검토할 필요가 있다. 이를 위해 수치 해석을 수행하여 클램프의 최대 마찰 저항력과 와이어 손상 가능성을 평가하였다. 분석 결과, 보조 클램프(Temporary clamp)에서 발생하는 최소 마찰 하중은 약 34.6 kN으로, 이는 케이블과 보호 기자재의 목표 중량인 30 kN보다 약 14% 높은 수준임을 확인하였다. 또한, 영구 클램프 체결 시 클램프에서는 최대 414.4 MPa, 와이어에서는 최대 881.3 MPa의 응력이 발생하는 것으로 나타났다. 와이어의 최대 응력은 소재의 인장 강도를 초과하였으나, 이는 국소적인 응력 집중 현상으로 판단되었으며, 좌굴 및 변형은 관찰되었으나 파단 가능성은 낮은 것으로 확인되었다.

Keywords: 행오프 클램프(Hang-off clamp), 해저케이블(Submarine cable), 최대마찰저항력(Maximum static frictional force), 최대응력(Maximum Stress)

전력 발전의 중요성은 경제, 여가, 생산, 소비의 확대로 그 중요성이 커지고 있다. 세계적인 전력소비량은 친환경에너지의 운송, 저장, 소비 규모확대와 이를 활용한 AI, 전기자동차와 같은 전기의존기술의 발달로 인해 더욱 증가세를 보이고 있다[1].
풍력, 파력, 조력, 태양광 등의 신재생 에너지의 발전과 함께 전력 공급량을 늘리기 위한 다양한 방법들이 제시되고 있다. 전력공급 추세에 힘입어 풍력발전단지 또한 증가하고 있으며 해상풍력의 경우 육상에 비해 설치공간, 난류, 소음, 풍력자원 등의 장점으로 20년동안 수요가 급격히 증가하였다[2].
해저케이블의 경우 해양환경으로부터 반복하중, 부식, 장소의 특수성으로 인한 설치비용 증가 등의 단점이 보고되고 있으나 보호기자재 등의 발전으로 인해 단점을 보완하는 방법들이 제시되고 있다. 또한 해저케이블의 매설 방법의 발달과 설치방법의 고도화로 인해 해저케이블 설치 시의 단점이 보완되고 있다.
행오프 클램프(Hanf-off clamp)의 경우 해저케이블 설치 시 케이블과 보호기자재의 하중을 지지하는 역할을 한다. 이는 케이블에 직접적으로 체결되면서 영구 클램프(Permanent)까지 케이블 및 관련 기자재에 대한 중량을 지지하는 역할과 케이블 말단의 와이어를 압착하여 영구적으로 고정하는 역할을 한다.
실물을 이용한 실험의 경우 실제환경을 반영하여 결과를 도출하는데 신뢰성을 가질 수 있으나 실물 실험에 관련한 제작 및 제어와 반복실험 등에 있어 시간적, 물리적, 비용적인 어려움을 가진다. 이러한 단점들로 인해 기본 및 상세 설계과정에서는 수치 해석 및 시뮬레이션을 통한 설계 인자를 분석하여 설계 타당성을 도출한다. 특히 이방성과 같은 물성치 부여와 좌굴 압력 예측, 하중조건 변경, 비선형거동 예측과 같은 인자들을 반영하여 설계 타당성을 볼 수 있는 용이성으로 인해 복합재료 분야에서는 설계 시 수치 해석 및 시뮬레이션의 활용성이 증가하고 있다[3-8].
본 연구에서는 유연 입상 설치 시스템(Flexible Pull-in Installation System, FPIS)에서 해저케이블에 사용되는 행오프 클램프를 대상으로 수치해석적 방법을 통해 기계적 거동을 살펴보았다. 행오프 클램프는 복합재료에서 활용될 수 있는 PU 소재와 부재물들을 포함하는 piggy back clamp로서 수치해석적 방법론을 통한 기계적 거동 분석은 필수적이고 piggy back clamp의 구속력 및 와이어 안전성에 대해 분석하였다. 수치 해석적 방법을 통해 클램프에 가해지는 추가 하중을 구현하였고 클램프의 최대 마찰 저항력과 최대응력을 확인하였다. 이를 통해 와이어 손상 가능성을 평가하였고 볼트체결강도와 와이어 안전성을 도출하였다.

2.1 배경
보조 클램프 구속력은 슬립이 발생되는 최대 마찰 저항력 이하의 중량이 가해질 경우 구속된다.
만약 구속력을 위해 클램프 체결 볼트의 체결강도를 높인다면 케이블 외곽의 와이어 및 클램프에 손상이 발생하기 때문에 적절한 구속력의 확보와 체결강도 산정이 필요하다. 클램프 체결 볼트의 체결강도의 경우 케이블 및 보호기자재의 중량 30 kN 이상인 최대마찰 저항력을 가졌을 경우 충분한 구속력을 지닌다. 클램프 와이어의 경우 영구 클램프 체결 시 압착으로 인한 파단여부를 통해 파단 및 손상여부를 확인할 수 있다. 파단여부는 영구 클램프로 인해 와이어에 가해지는 국소적인 응력들을 구성재질의 인장강도 등과 비교하여 나타난 변형률과 변위를 통해 파악할 수 있다.
2.2 모델링
2.1.1 보조 클램프 모델링
보조 클램프의 경우 Fig. 1와 같이 슬립이 발생하지 않는 마찰하중을 도출하기 위해 와이어와 클램프를 중심으로 모델링하였다.또한, 케이블의 내부 구성요소는 해석의 수렴성을 위해 Dummy 모델로 가정하였으며, 재질은 강재(steel)로 적용하였다.
보조 클램프의 격자 생성은 Fig. 2와 같이 해석모델의 형상적 특징을 반영하여 격자를 구성하였다. 클램프는 Tetra 격자, 케이블은 Hexa 격자를 적용하였다. Dummy 모델의 경우 구조부재가 아니므로 격자 사이즈를 주요부재에 비해 큰 사이즈를 적용하였다.
2.1.2 영구 클램프 모델링
영구 클램프의 모델링은 Fig. 3과 같이 체결 후 추가적인 하중을 가해 하중에 의한 케이블 와이어의 변위 발생과 그로 인한 변형을 확인하기 위해 해석모델을 구성하였다. 1개의 외각와이어가 부담하는 외부하중으로 의한 파단, 파손 발생여부를 확인하고 와이어를 고정하기 위한 구조적 성능을 검토하기 위한 모델링을 진행하였다.
영구 클램프의 격자는 Fig. 4과 같이 모든 부재에 Hexa 격자를 적용하였다. 격자사이즈는 해석모델의 사이즈 및 접촉으로 인한 대변형 등을 고려하여 2 mm~4 mm로 설정하였다.
2.2 재료 물성치
두 클램프 및 외곽 와이어는 S355J2를 소재로 사용하였다. 일반적인 설계에서는 선형범위 내에서 해석을 수행하지만 본 연구에서는 압착 과정에서 발생되는 대변형에 따른 비선형성을 고려하기 위해 비선형 재료를 적용하였다. 재료 모델은 Table 1과 같이 항복강도는 355 MPa, Tangent Modulus는 1,450 MPa를 적용하였다.
케이블 중간 내용물인 Dummy 모델은 강재로 가정하여 선형재료를 적용하였으며, 모든 강재의 탄성계수(E)는 200,000 MPa, 포아송비(v)는 0.3을 적용하였다[9].
2.3 하중 및 경계 조건
2.3.1 보조 클램프
보조 클램프 접촉조건은 Dummy와 외곽 와이어와의 접촉조건을 고려하여 외곽 와이어를 케이블 중앙 내용물과 부착하는 Bonded Contact 조건을 부여하였다. 또한, 클램프와 외곽 와이어 간의 접촉은 구조거동을 고려하여 Frictional 접촉조건을 적용하였으며, 마찰계수는 강재와 강재 간 적용이 가능한 0.2로 설정하였다.
클램프의 돌기는 Fig. 5와 같이 클램프와 외곽 와이어의 접촉 특성 및 해석 수렴도를 높이기 위해 날카로운 돌기대신 둔각의 돌기로 수정하여 해석을 수행하였다.
클램프의 경우, 압착 후 케이블 및 보호기자재 중량인 30 kN의 하중이 적용될 때 클램프와 케이블 간 슬립이 발생되지 않는 구속력을 요구하지만 구속력이 너무 클 경우 외곽 케이블 와이어를 손상시킬 수 있는 위험성 때문에 최소 구속력을 도출하는 방향으로 구조해석을 수행하였다.
해석모델인 클램프와 와이어는 Fig. 6과 같이 해석시간을 단축하기 위해 xz-평면을 기준으로 대칭 모델을 적용하여 구조해석을 수행하였다. 또한, 비선형 재료 및 접촉을 적용 시 해석의 수렴성 문제로 인해 하중이 아닌 변위하중을 고려하여 해석을 진행하였다.
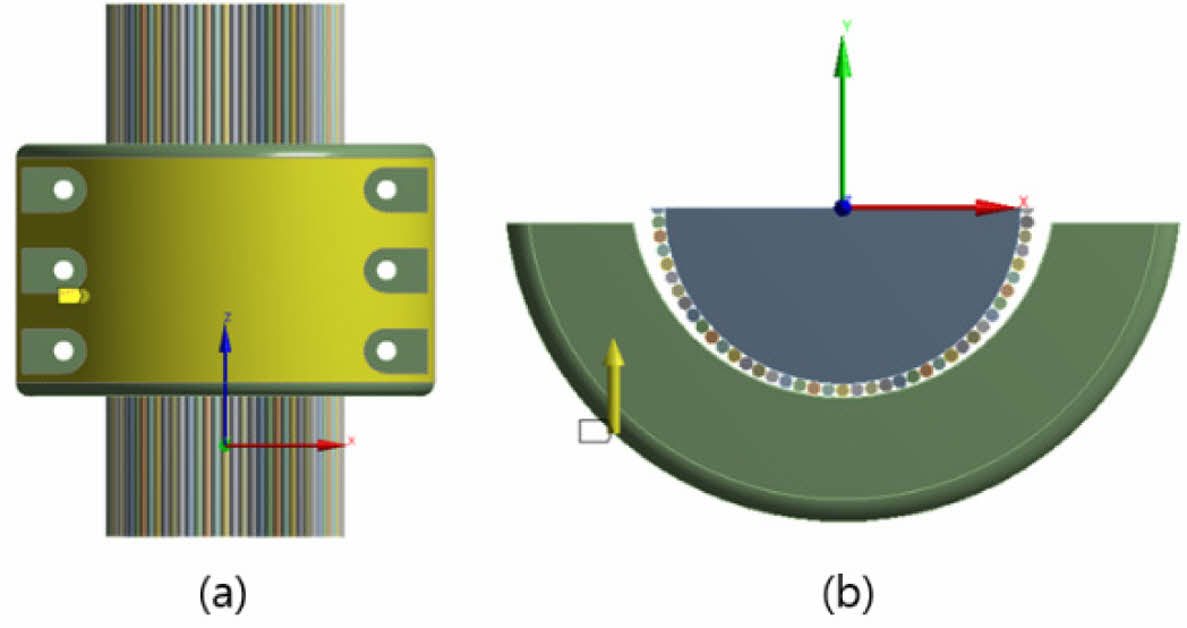
Fig. 6의 경우 압착하중으로 인해 발생하는 클램프의 수평 변위가 0~0.5 s일 때 클램프는 최대 0.17 mm 이동 후 같은 위치를 유지한다. 따라서 케이블에 상기의 수평 변위 조건을 적용 후 수직 변위를 적용하여 슬립이 발생하는 최소마찰하중을 검토하였다.
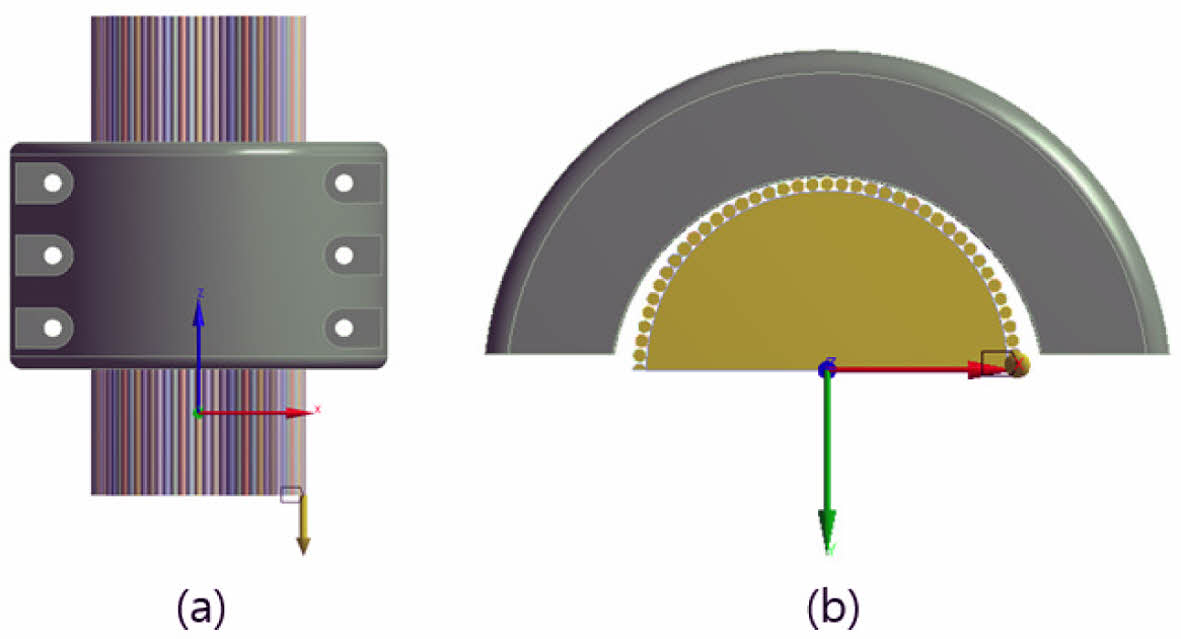
Fig. 7의 경우, 클램프에 압착 하중 이후 적용되는 케이블과 보호기자재 중량을 반영하여 케이블 해석모델 하부에 수직 변위를 최대 5 mm로 적용하였다.
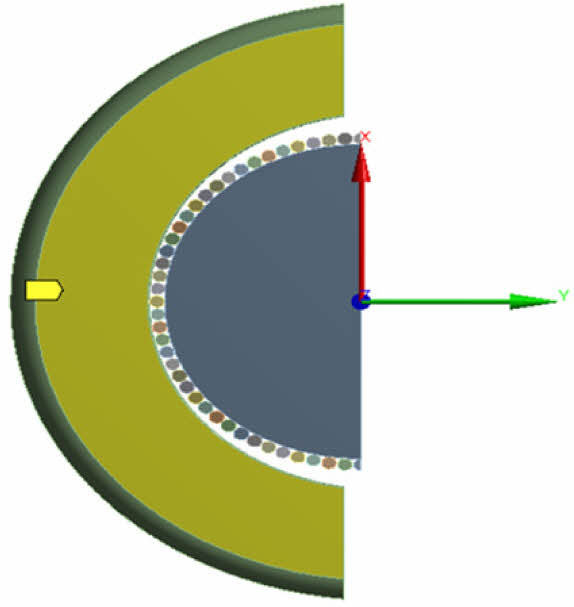
Fig. 8는 보조 클램프 해석의 경계조건을 나타내며, 클램프의 하부면과 베이스 플레이트가 접하는 면을 경계조건으로 적용하였다.
경계조건은 변위를 제어하여 클램프가 압착되는 방향을 제외하고 모든 변위(x, z축)를 제어하였다.
2.3.2 영구 클램프
영구 클램프는 Fig. 3과 같이 클램프의 체결 후 추가 하중에 대한 슬립발생 여부를 판단하기 위해 수행하였다.
해석시간, 수렴성 등을 고려하여 케이블 외곽 와이어 1개가 부담하는 하중에 대한 구조성능을 검토하였다. 해석모델의 접촉조건은 클램프와 외곽 와이어 간의 구조거동을 고려하여 슬립이 발생할 수 있는 Frictional 접촉조건을 고려하였으며, 마찰계수는 강재와 강재가 적용이 가능한 0.2를 적용하였다. 영구 클램프 체결 후, 자중으로 인한 추가 하중은 20 kN이 되어야 한다. 이는 클램프 압착 후 80개의 외곽 와이어에 20 kN의 수평하중을 적용하여도 케이블이 슬립 또는 파단이 발생되지 않도록 설계하여야 한다는 의미이다.
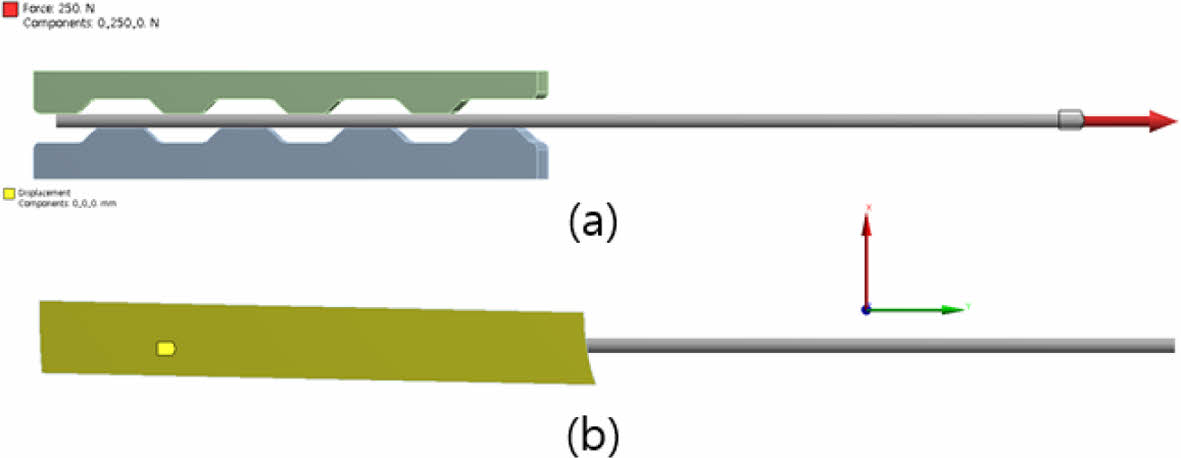
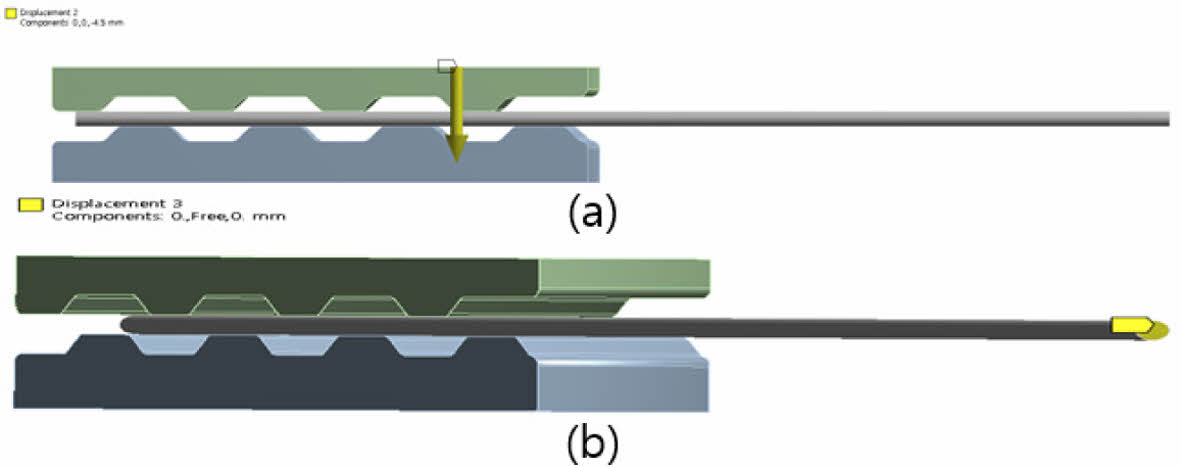
Fig. 9과 Fig. 10는 각각 수직, 수평 방향의 적용하중과 구속조건을 나타내며 클램프의 압착하중에 따라 발생되는 변위를 역으로 적용하였다. 클램프는 0.5 s 시간 내 최대 4.5 mm 압착 후 케이블에 수평 하중을 적용하여 구조거동을 검토하였다. 클램프 압착 하중 이후 적용되는 20 kN의 추가하중을 구현하는 방식은 수평하중을 80개의 외곽 와이어 하단에 중량 분담율이 동일한 것으로 가정하여 와이어당 250 N의 하중을 적용하는 방식을 사용하였다.
해석의 경계조건은 Fig. 9(b)와 같이 클램프 하부의 모든 방향에 대하여 변위(x, y, z축)를 제어하였다. 클램프 압착 시 와이어 단부의 수직 변위 및 회전 발생을 제어하기 위해 Fig. 10(b)와 같이 와이어 단부의 x와 z축을 제어하였다.

3.1 보조 클램프
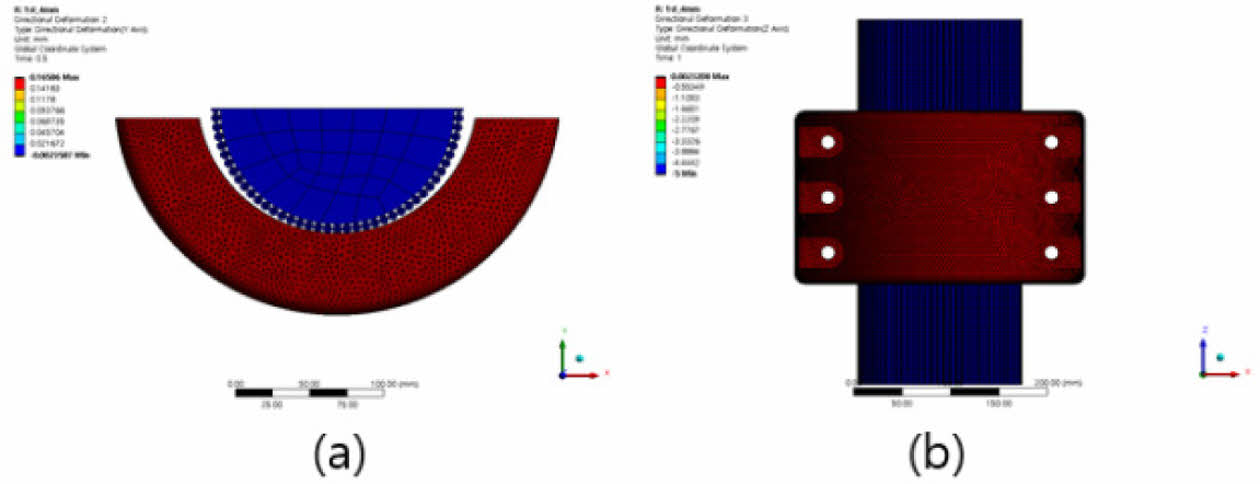
변위로 인한 수평 및 수직 변위 분포의 경우 Fig. 11에서 볼 수 있다. 수평 변위의 경우 Fig. 11(a)와 같이 0.5 s 시간 내에서 최대 0.165 mm, 수직 변위의 경우 Fig. 11(b)와 같이 0.5 s와 1.0 s에서 최대 5.0 mm 나타낸다.
Fig. 12은 stress 분포를 나타내며, 클램프에서 최대 381.3 MPa 항복강도 이상의 응력이 발생되고 이는 클램프의 압착하중에 따른 압축응력으로 인한 변형으로 확인되었다.
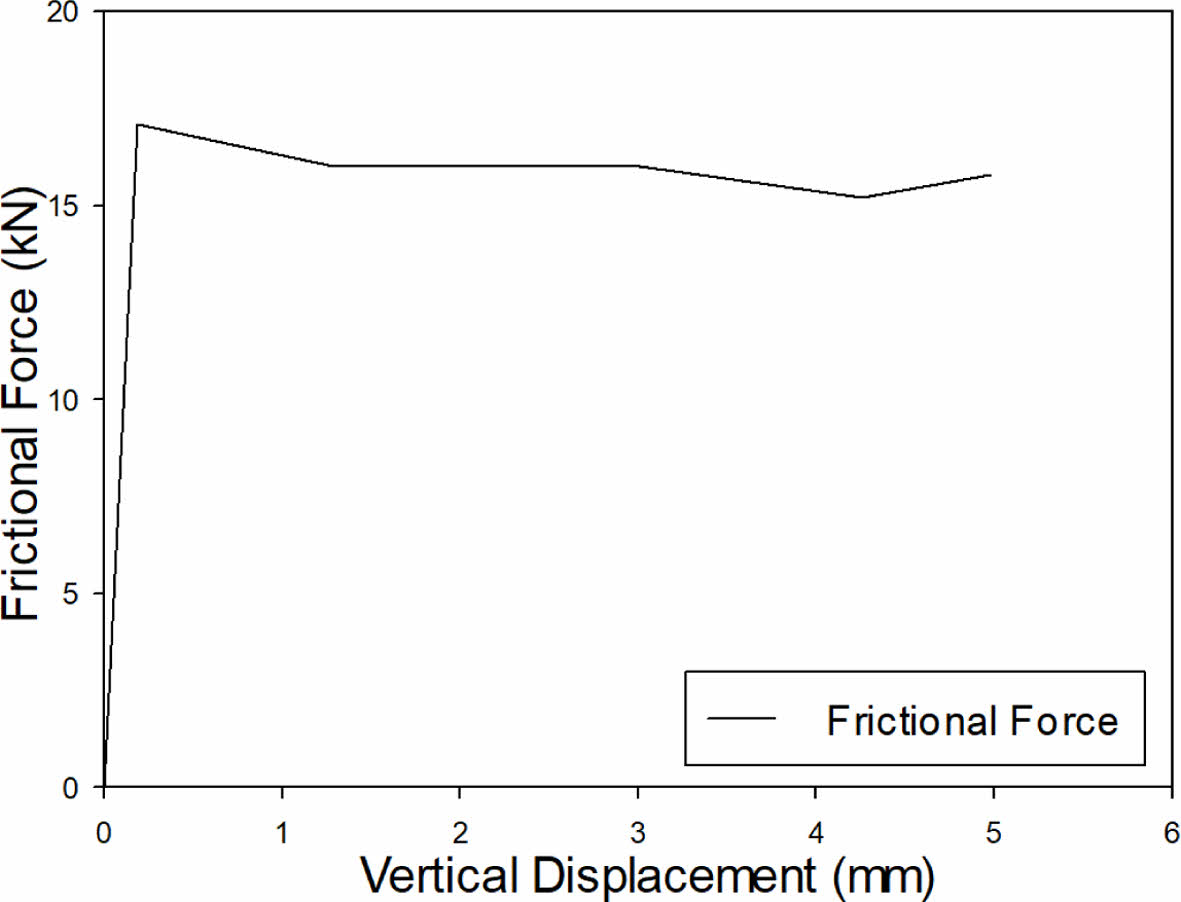
Fig. 13은 클램프 압착 후 케이블에 작용하는 수직 변위로 인해 발생되는 마찰하중을 나타내며, 마찰하중의 크기는 클램프에 작용하는 케이블 및 보호기자재의 중량과 같다. 와이어에서 슬립이 발생되는 최소 마찰하중은 약 17.2 kN으로 대칭모델인 것을 고려할 때 약 두 배인 34.4 kN으로 케이블 및 보호기자재 목표중량(30 kN)보다 약 14% 여유가 있는 것을 확인할 수 있다.
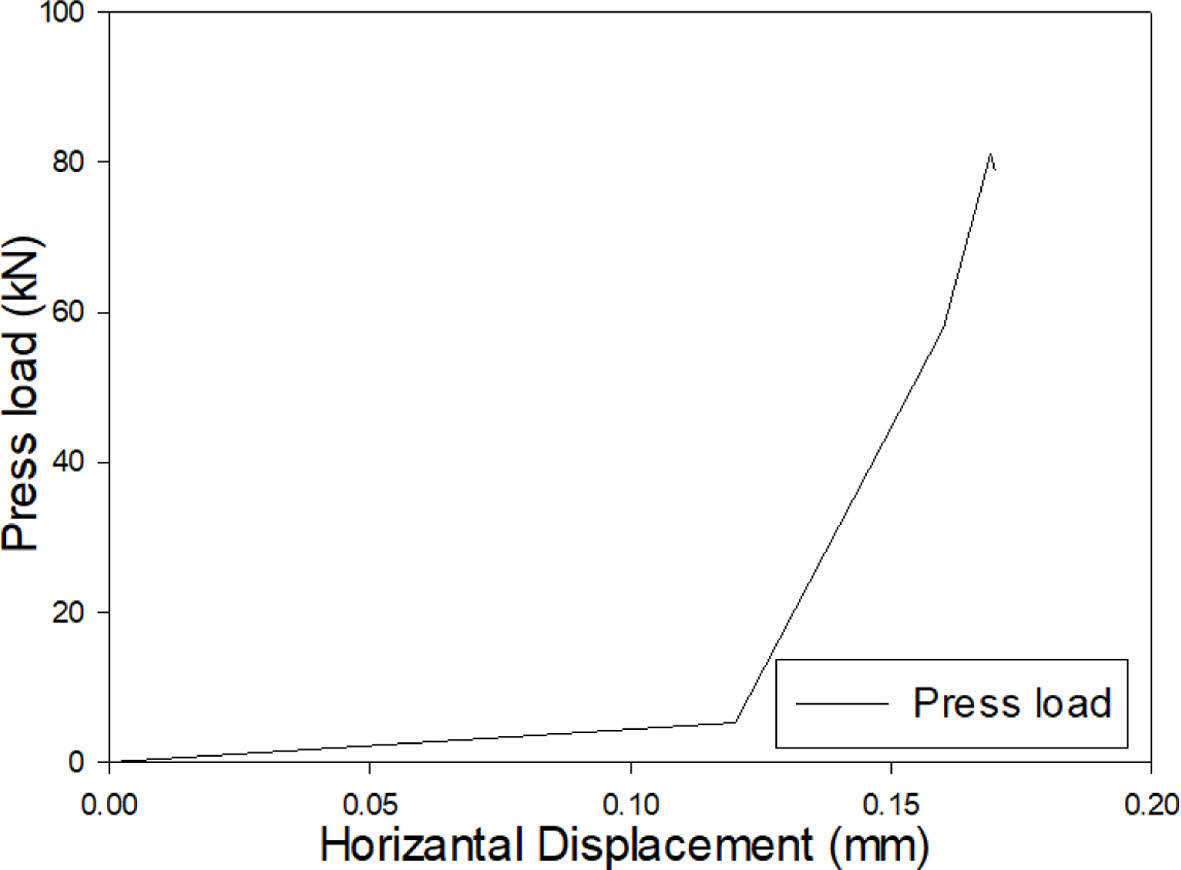
Fig. 14은 클램프 체결을 위한 볼트 프리텐션(pretension)을 도출하기 위한 압착하중으로 최대 약 81.3 kN를 보였으며 대칭모델을 고려할 때 두 배인 162.7 kN를 나타낸다. 즉 총 6개의 볼트를 고려하다면 볼트당 약 27.1 kN이 필요한 것을 알 수 있다.
3.2 영구 클램프
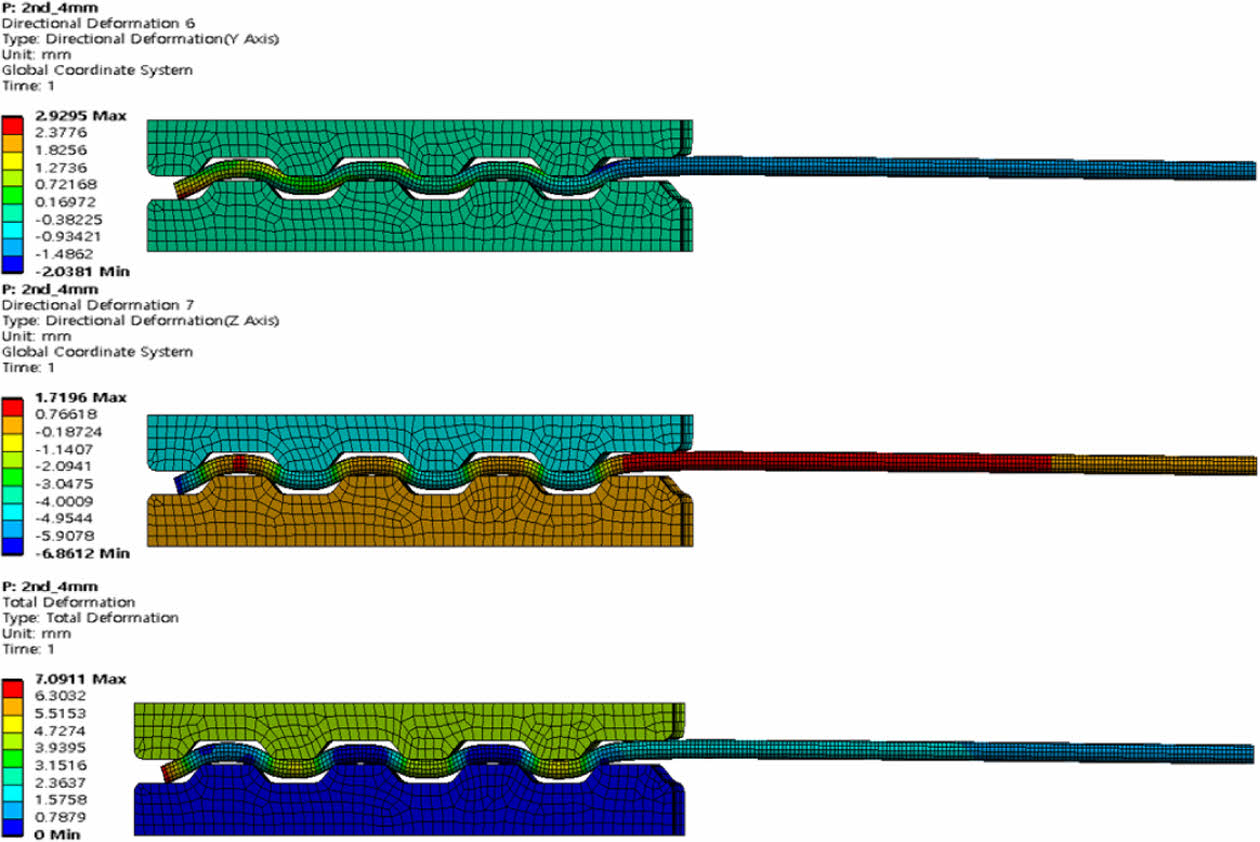
변위로 인한 수평, 수직 및 Total 변위 분포의 경우 Fig. 15에서 확인할 수 있다. 특히 Fig. 15(a)에서는 와이어에서 발생되는 수평 변위가 매우 미소한 것을 확인할 수 있다.
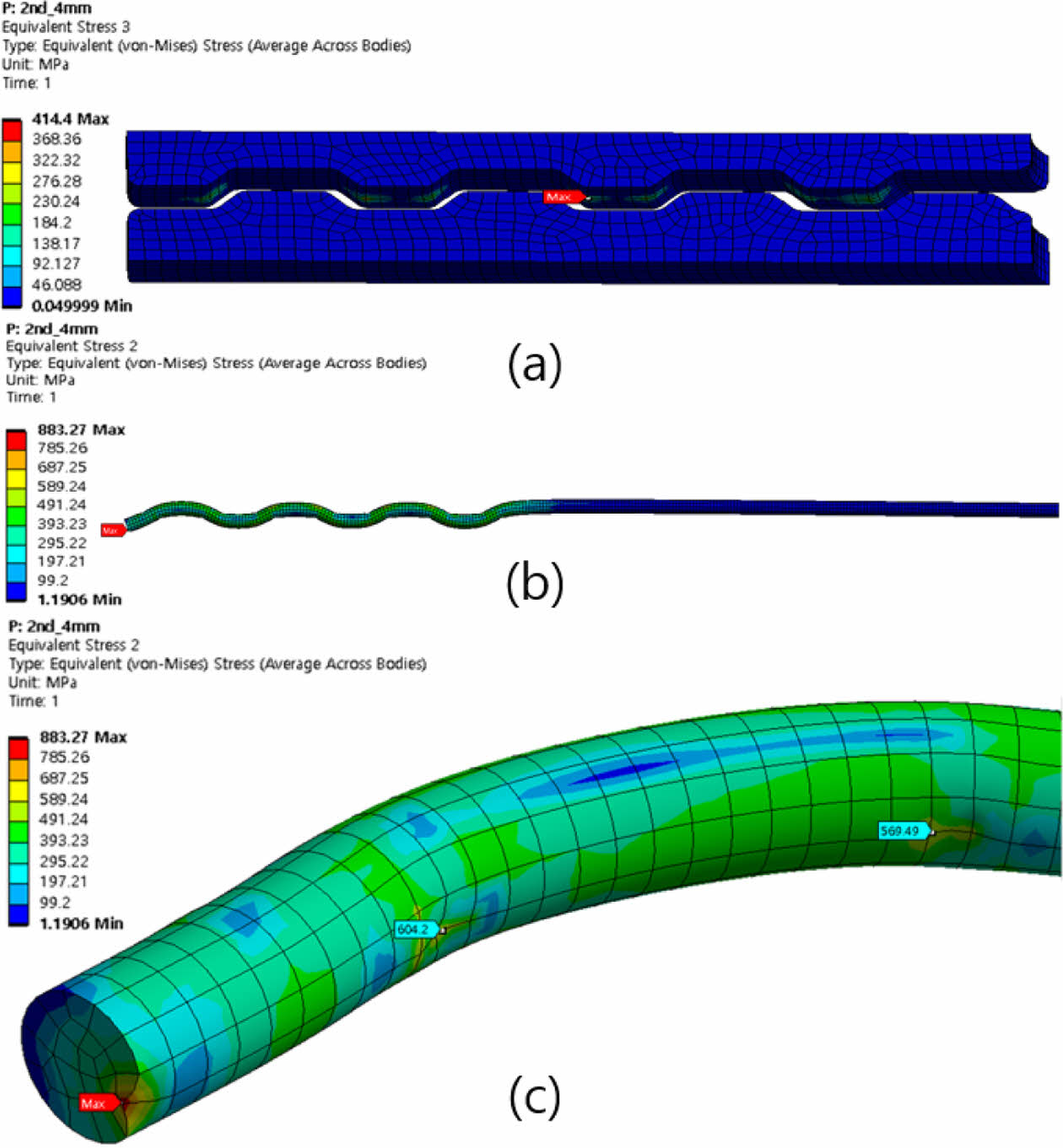
Fig. 16은 해석모델에 발생되는 Von Mises stress 분포를 나타내며 클램프에서는 최대 414.4 MPa, 와이어에서는 최대 881.3 MPa을 보인다. 와이어의 경우 재료의 인장강도 이상의 응력이 발생되는 것을 확인할 수 있다.
결과로 나타나는 거동은 클램프의 압축응력으로 인한 변형으로 판단되며, 와이어의 경우 Fig. 16(c) 같이 단부의 변형에 따른 응력집중으로 판단된다.
그 외 대변형이 발생되는 위치에는 S355J2의 인장강도 600 MPa[10] 이상인 최대 604.2 MPa의 응력이 발생되어 부재응력의 특성에 대한 검토가 필요한 것을 알 수 있다.
Fig. 16(c)의 말단부 및 첫 굴곡 지점을 제외한 굴곡점의 경우 인장강도 이상의 응력이 발생하지 않음을 알 수 있었다. 또한 클램프 중심으로 와이어를 통과시키기 때문에 말단분의 와이어로 인한 높은 압축응력과 첫 굴곡점의 응력집중 현상으로 인한 높은 응력이 발생하지 않을 것으로 예상된다. 하지만 와이어의 굴곡점마다 응력 집중 현상이 발생하여 좌굴 및 찌그러짐이 발생할 수도 있다. 따라서 응력집중으로 인한 손상의 가능성 등은 클램프의 간격 및 사이즈 조정하여 손상위험성을 낮추는 추가 연구가 진행되어야 될 것으로 보인다.

본 연구에서는 유연 입상 설치 시스템(Flexible Pull-in Installation System, FPIS)에서 해저케이블에 사용되는 행오프 클램프의 구속력 및 와이어 안전성을 분석하였다. 본 연구의 결과들은 아래와 같이 정리할 수 있다.
보조 클램프에 최소 162.7 kN 프리텐션(pretension)을 적용할 경우 케이블 및 보호기자재의 중량 3 ton에 대하여 슬립이 발생되지 않는 것으로 계산되었다. 볼트의 개수를 고려할 경우 하나의 볼트에 약 27.1 kN이 필요하다는 것을 알 수 있었다.
영구 클램프 해석의 경우 외곽 와이어 클램프 압착으로 인해 국부 대변형은 미소하게 발생되지만, 전반적으로 압축거동 중심으로 와이어 파단은 발생되지 않는 것으로 판단된다. 하지만 클램프 사이즈 조정을 통해 접촉면적이 증가시켜 국부 손상의 완화가 가능한 것을 알 수 있었다.
영구 클램프 체결 후 추가되는 하중 20 kN에 대하여 케이블의 외곽 와이어는 슬립이 발생되지 않는 것을 확인하였다.
클램프 압착에 따른 부재의 대변형으로 인해 발생되는 Von Mises 응력은 압축의 영향이 지배적인 것을 알 수 있었고 국부 좌굴 및 찌그러짐이 발생될 가능성이 있는 것을 알 수 있으나 파단과 같이 부재의 구조거동에 미치는 영향은 적을 것으로 판단된다.
본 연구의 결과는 유연 입상 설치 시스템(Flexible Pull-in Installation System, FPIS)에서 해저케이블에 사용되는 행오프 클램프의 거동과 이로 인한 신뢰성을 판단하는데 중요하게 사용될 수 있는 결과들이다. 또한 본 연구의 방법론은 행오프 클램프 뿐 아니라 복합재료를 활용한 해양 구조물 등의 시스템 설계 시 참고자료로 활용될 수 있을 것으로 기대한다.

본 연구는 2021년도 정부(산업통상자원부)의 재원으로 한국에너지기술평가원의 지원을 받아 수행된 연구임(20213000000020, 해상풍력단지 해저 전력망 구축을 위한 핵심기자재 및 평가 기술 개발) 수행된 것이며, 지원에 대해 진심으로 감사드립니다.