Carbon fiber composites has higher specific strength and specific stiffness compared to the conventional metals, making it favorable for lightweight design. However, achieving the required level of surface accuracy and stability has been challenging, have limited its application in optical mirror fabrication. In this paper, diameter of 200mm carbon fiber composite aspherical mirror was optimized for reducing its mass and WFE. To reduce computational time, design of experiments (DOE) and the Kriging method were used to construct meta-models, and multi-objective particle swarm optimization (MOPSO) was employed for optimization. Optimal design of the mirror model was determined based on the knee point obtained from the Pareto front. Compared with the initial design model, the mass reduced by 45.3%, and the WFE reduced by 32.5%. The proposed optimization design method and results can serve as a reference for the development of carbon fiber composite mirrors.

탄소 섬유 복합재는 일반 금속 대비 비강도(specific strength)와 비강성(specific stiffness)이 높아, 경량 설계에 유리한 재료이다. 그러나 필요 수준의 표면 정확도와 안정성 확보에 어려움이 있어, 광학 반사경 제작에 적용하는 데 한계가 있었다. 본 연구에서는 직경 200mm의 탄소 섬유 복합재 비구면 반사경을 대상으로 질량과 파면 오차(WFE)를 최소화하는 최적화 설계를 수행한다. 계산 시간을 줄이기 위해 실험계획법과 크리깅(Kriging) 기법을 사용하여 메타모델을 구축하고, 다목적 최적화를 위해 다목적 입자 군집 최적화(MOPSO)를 활용하였다. 반사경의 최적모델은 파레토 전선에서 도출된 무릎점(knee point) 데이터를 기반으로 결정되었으며, 그 결과 초기 모델 대비 질량은 45.3%, WFE는 32.5% 감소하였다. 본 논문에서 제안된 최적화 설계 방법과 결과는 탄소 섬유 복합재 반사경 개발에 대한 참고 자료로 활용될 수 있다.

Keywords: 탄소 섬유 복합재(Carbon fiber composite), 비구면 반사경(Aspherical mirror), 파면오차(Wavefront error), 크리깅(Kriging), 다목적 입자 군집 최적화(Multi-objective particle swarm optimization)

최근 우주 산업의 발전과 위성 시장의 확대에 따라 높은 해상도, 넓은 시야각, 경량 특성을 갖춘 반사경에 대한 수요가 증가하고 있다. 다양한 반사경 유형 중에서 비구면 반사경은 빛을 굴절시켜 구면 수차를 보정하고 보다 정밀한 광학 조정을 가능하게 하기 때문에 평면 반사경보다 선호된다. 광-기계 구조(optical-mechanical structure)에서는 광학 성능을 유지하면서도 발사 비용을 최소화하기 위해 경량 설계가 필수적이다[1]. 선명하고 넓은 시야를 확보하기 위해 반사경은 낮은 파면 오차(wavefront error, WFE)를 유지하면서 충분한 구경을 확보해야 한다. 또한, 위성 발사 비용 절감을 위해 경량화가 필수적이다. 따라서 WFE를 최소화하면서도 가벼운 비구면 반사경의 개발이 필요하다.
반사경은 일반적으로 초저팽창(Ultra-low expansion, ULE) 유리, 실리콘 카바이드(SiC), 베릴륨(Be), 제로더(Zerodur) 등의 소재로 제작되어 왔다. 이러한 재료들은 높은 비강성 (specific stiffness)과 우수한 열 적응성을 제공하며, 나노미터 수준의 표면 거칠기를 구현할 수 있는 장점이 있다[2,3]. 그러나 밀도, 강성, 강도 등의 한계가 있으며, 벌크 형태의 제조 공정에서 리브(rib) 두께의 제약으로 인해 추가적인 경량화가 어렵다. 반면, 탄소 섬유 복합재는 높은 비강도 및 강성을 가지며, 기존 재료보다 유리한 광학적 특성을 제공한다. 탄소 섬유를 기반으로 하는 여러 복합재에 대한 내구성 평가, 거울 프로토타입 설계, 제작 및 실험을 통해 우주용 반사경 소재로서의 적합성이 입증되었다[4-6]. 또한, 얇은 탄소 섬유 복합재를 활용하면 곡률 반경을 조절할 수 있는 변형 가능한 반사경의 개발에 사용 가능함도 확인되었다[7,8].
광학 반사경의 경량 설계를 위해 많은 연구들이 수행되어 왔다. 구조적인 측면에서의 경량화를 위해, contoured-back solid, 오픈-백(open-back), 샌드위치 구조를 채택하거나[9-12], 위상최적화를 활용하는 연구가 진행되었다[13,14]. 또한, 반사경 패널의 두께 Rib의 두께와 같은 설계 파라미터를 최소화하여 반사경의 패널 질량을 최소화하는 연구도 수행되었다[15]. 더 나아가, 매개변수의 파레토 전선을 도출하여 SiC/Al 반사경의 질량과 RMS (Root mean square) 오차를 개선하는 연구도 진행되었다[16]. 그러나, 이러한 선행 연구에도 불구하고, 탄소 섬유 복합재를 소재로 한 반사경의 경량설계에 대한 연구는 아직 부족한 실정이다.
본 연구에서는 탄소 섬유 복합재의 우수한 성능을 기반으로 하는 직경 200mm의 비구면 반사경을 최적화한다. 설계 과정에서 달성해야 하는 질량과 WFE의 최소화는 목표 함수 간의 복잡한 상충 관계와 계산 복잡도로 인해 다중 목적 최적화가 필수적이다. 따라서, 최적화를 위해 실험계획법과 Kriging 기법을 활용하여 메타모델을 생성하고, 다목적 입자 군집 최적화(Multi-objective particle swarm optimization, MOPSO) 알고리즘을 사용하여 최적해를 도출하였다. 마지막으로, 최적화 결과를 유한요소해석과 비교하여 신뢰성을 검증하였다.

2.1 재료 및 적층 순서
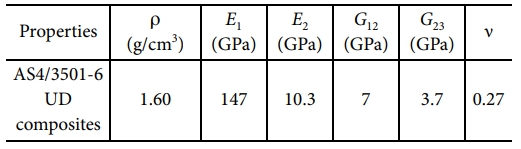
광학 반사경은 일반적으로 축대칭 구조로, 안정성을 유지하면서 변형을 최소화해야 한다. 복합재의 준등방성 적층판 외부 하중에 균일하게 반응하여 이러한 요구를 효과적으로 충족시킨다[17]. 반사경의 재료로 AS4/3501-6 단방향(UD) 프리프레그가 사용되었으며, 경화된 플라이 두께의 공칭값은 0.125mm이다. [0/±45/90]_s에 따라 적층을 하였으며, 이는 준등방성(quasi-isotropic properties)을 제공함과 동시에 스프링백(spring-back) 효과를 최소화하는 역할을 한다. 해당 적층 순서에 따라 8겹을 적층하면 총 두께가 1mm인 라미네이트가 형성되며, AS4/3501-6 복합재의 물성은 ASTM D3039 및 ASTM D3518을 기반으로 한 실험을 통해 얻었다.
2.2 비구면 반사경 설계
탄소 섬유 복합재는 벌크 형태로 제조하기 어려워 반사경 설계에서는 얇은 프리프레그 층을 적층하는 방식이 주로 사용된다. 이때, 구조적 강성과 열 변형 안정성을 확보하기 위해 허니콤 코어 샌드위치 구조나 그리드 보강 구조가 적용된다. 허니콤 코어 샌드위치 구조는 높은 강성을 제공하고 열 변형을 최소화하는 장점이 있으며[18], 그리드 보강 구조는 샌드위치 구조뿐만 아니라 오픈백 구조에도 활용될 수 있다. 특히, 상하 패널과 중간 지지체 모두에 탄소 섬유 복합재를 사용하면, 패널과 지지체 간 열팽창 계수 차이를 제거할 수 있다. 또한, 허니콤 구조와 비교했을 때 그리드 보강 구조는 강성 분포가 균일하며, 허니콤 구조에서 발생할 수 있는 평면 외 왜곡 문제를 효과적으로 방지할 수 있다[19].
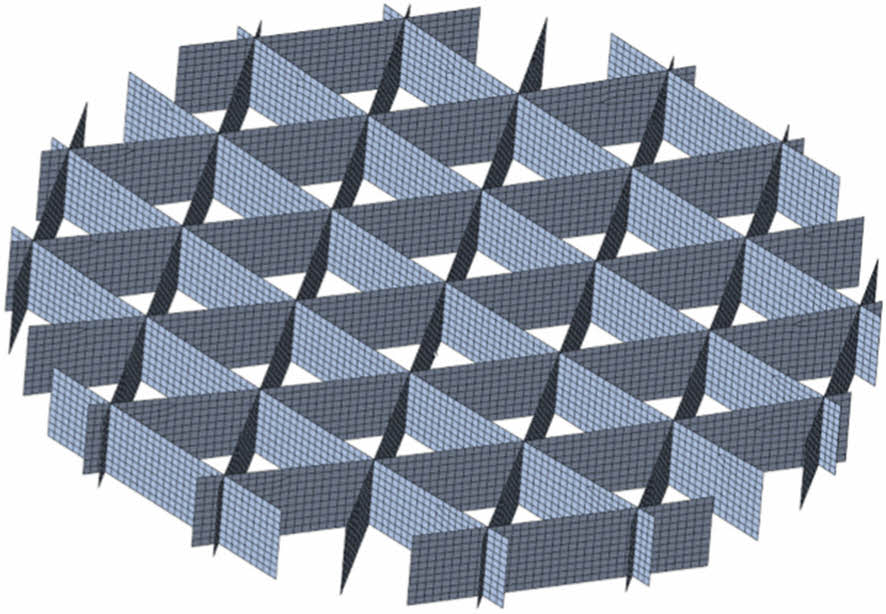
이러한 특성으로 인해, 반사경은 두 개의 패널과 하나의 그리드 코어로 구성된 그리드 보강 구조를 채택하였다. 일반적으로 그리드 보강 구조는 삼각형, 사각형, 육각형과 같은 패턴을 활용한다. 비구면 반사경의 경우 곡면 형상으로 인한 설계 복잡성으로 육각형 패턴을 적용하는 데 어려움이 있다. 반면, 삼각형 패턴은 육각형 패턴에 비해 제작이 용이하며, 사각형 패턴보다 우수한 측면 강성을 제공하는 것으로 알려져 있다[20]. 따라서 반사경과의 호환성을 고려하여, 그리드 보강 코어는 Fig. 1과 같이 삼각형 패턴을 적용하였다.
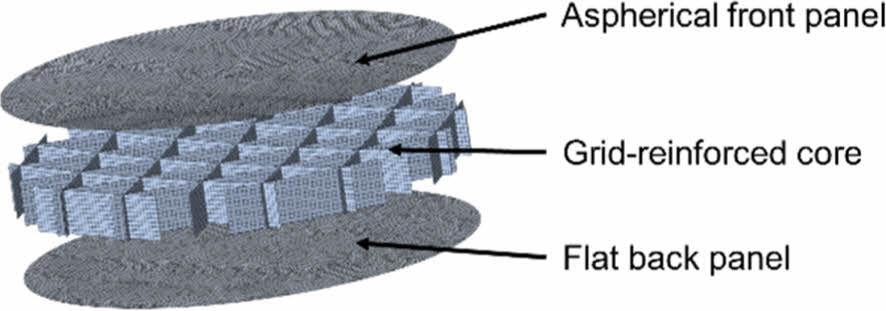
비구면 반사경의 구조는 Fig. 2에 나타난 바와 같이 비구면 패널, 평면 패널, 그리드 보강 코어로 구성된다. 비구면 전면 패널은 식 (1)로 나타낸 sagitta 방정식을 사용하여 형상을 근사하여 설계된다.



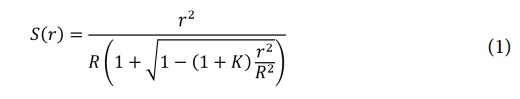
여기서, R은 광학 표면의 곡률 반지름, r은 광축에 따른 변위(거리), K는 원뿔 상수를 의미한다.
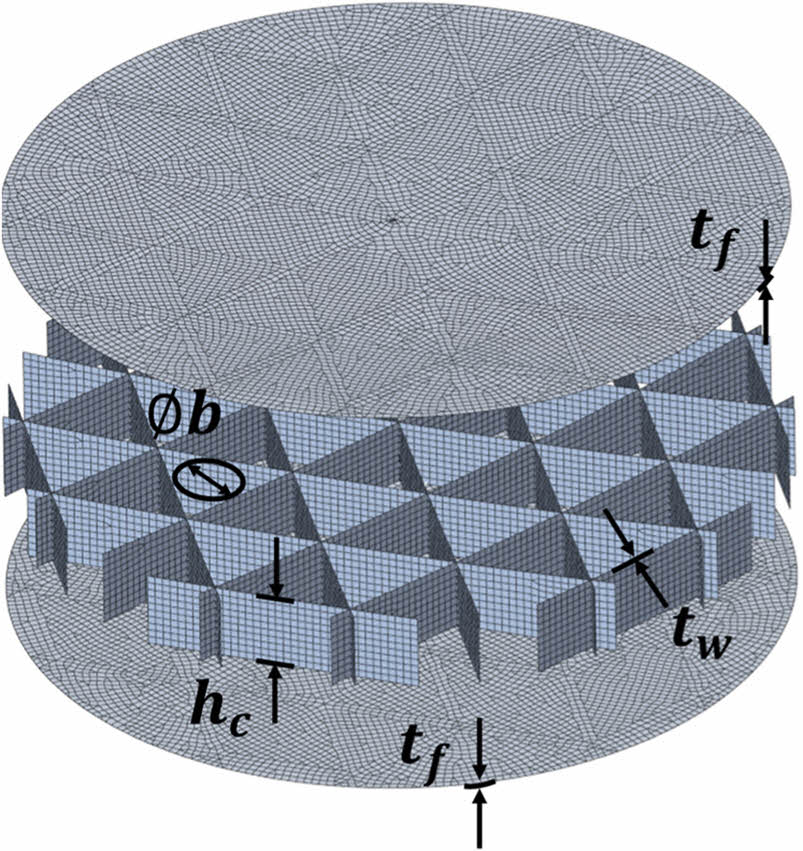
반사경의 표면 변형은 광학 시스템에서의 위상 오차인 WFE를 직접적으로 유발하므로, 굽힘 강성(flexural rigidity)은 WFE의 특성을 효과적으로 반영하는 지표로 간주된다. 이러한 점에서 굽힘 강성 극대화를 목표로 하는 전통적인 그리드 보강 반사경 설계 방식과 마찬가지로, 패널 두께(t_f), 그리드 두께(t_w), 그리드 높이(h_c), 그리드 내접원의 직경(b)을 주요 설계 변수로 정의한다[21]. 설계 변수는 Fig. 3과 같다.
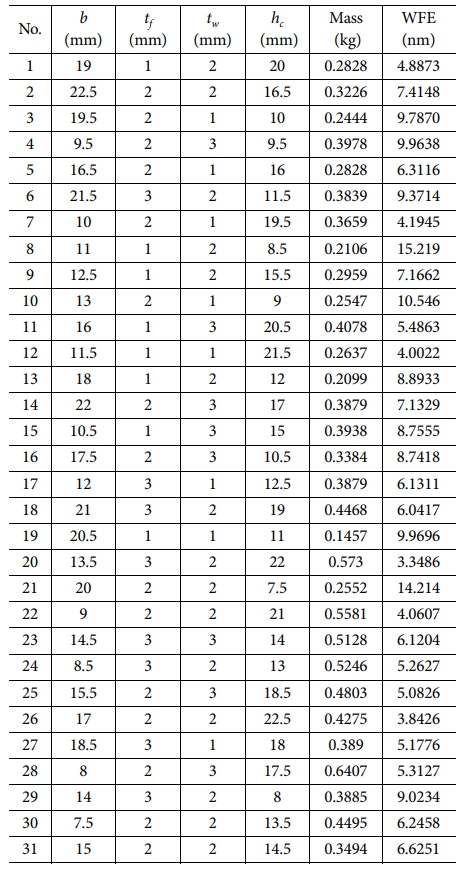
비구면 반사경을 설계하기 위한 초기 데이터는 Table 1에 제시되어 있다.
2.3 유한요소해석
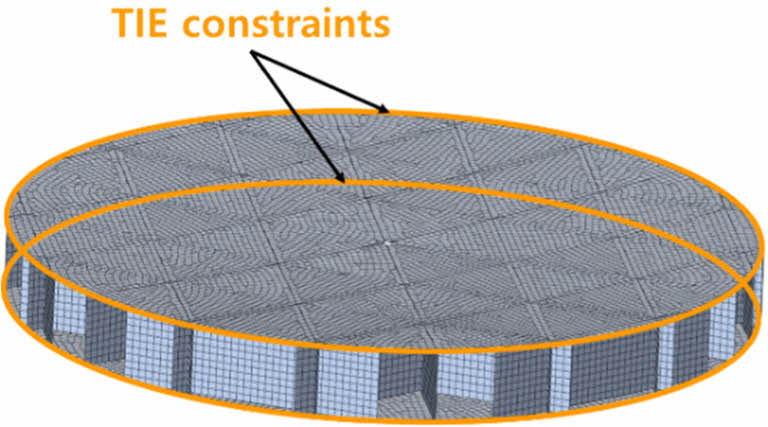
비구면 반사경의 유한요소 모델은 NX UG를 사용하여 모델링하고, Hypermesh를 이용해 메쉬 처리되었다. 유한 요소해석은 Optistruct에서 수행되었다. 적층을 모델링하기 위해 CQUAD8 요소가 사용되었다. 메쉬 수렴성을 평가한 후, 요소 크기는 2mm로 선정하였다. 초기 모델은 34,936개의 요소와 104,468개의 절점으로 구성된다. Fig. 4에 나타난 바와 같이, 패널과 그리드 강화 코어 사이에는 TIE 제약 조건이 적용되었다.
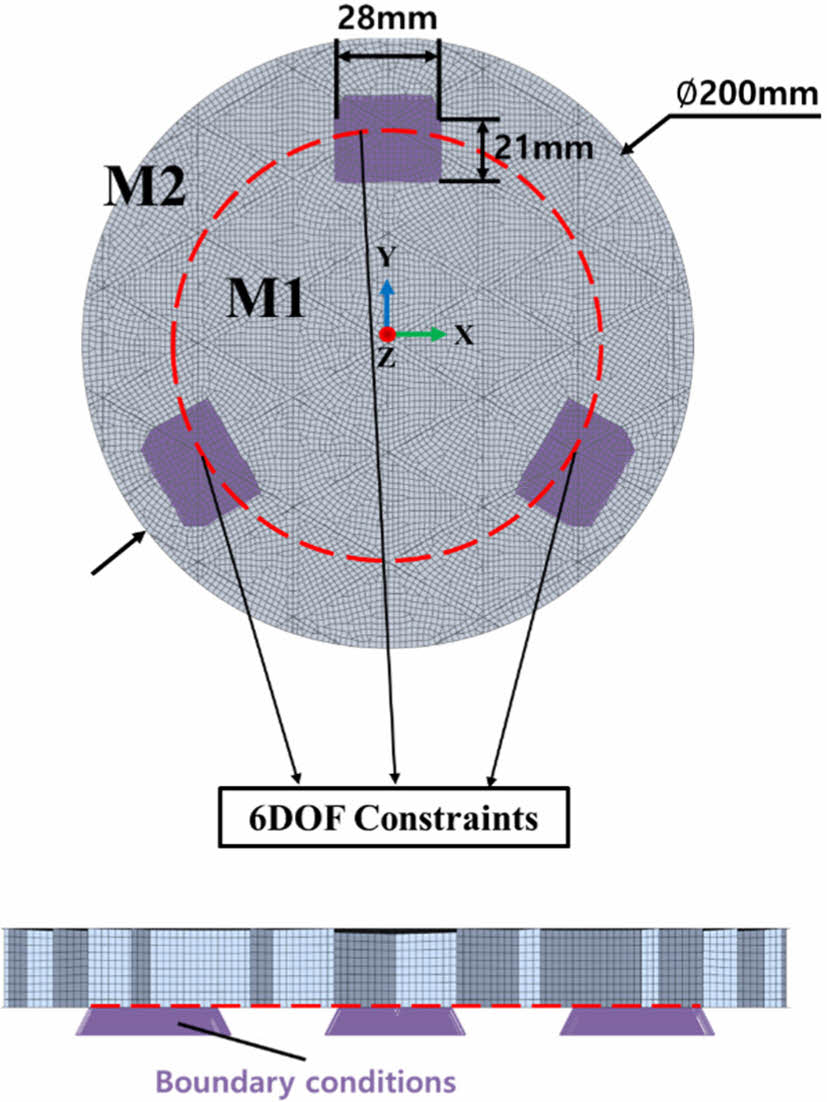
반사경의 정밀한 위치 제어와 설치 또는 열 응력에 대한 표면 형상 정확도를 유지하기 위해 6자유도의 엄격한 제약이 필요하다[16]. 비대칭을 최소화하고 자중으로 인한 변형을 줄이기 위해, Fig. 5에 나타낸 바와 같이, 반사경의 내부 부분(M1)과 외부 부분(M2)의 질량이 동일할 때, Flexure가 M2의 외접원을 따라 장착된다. 반사경의 후면 패널에는 세 개의 Flexure가 원주 방향으로 대칭적으로 배치된다. Flexure 부착 영역의 크기는 28mm × 21mm로 지정된다.
본 연구에서는 Flexure를 명시적으로 모델링하는 대신, 반사경의 후면 패널에 경계 조건을 적용하였다. 이러한 조건은 Flexure 부착 위치에서 6자유도를 모두 제약하여 반사경의 병진 운동과 회전 운동을 모두 제한한다.
또한, 자중에 의한 변형을 시뮬레이션하기 위해 비구면 전면 패널에 Z축 방향을 따라 1G 중력 하중이 적용되도록 하였다.
2.4 비구면 반사경 최적화
반사경의 목표 함수인 질량과 파면 오차(WFE)는 본질적으로 상충 관계에 있다. 한 가지를 최적화하면 다른 한 가지가 희생되기 마련이며, 두 목표를 동시에 최적화하는 최적 솔루션을 도출하는 것은 어렵다. 이러한 문제를 해결하기 위해, MOPSO 알고리즘을 활용한 다목적 최적화가 수행되어 파레토 전선 상의 최적 솔루션을 식별한다. 탄소 섬유 복합재 비구면 반사경의 최적설계는 식 (2)에 제시되어 있다.



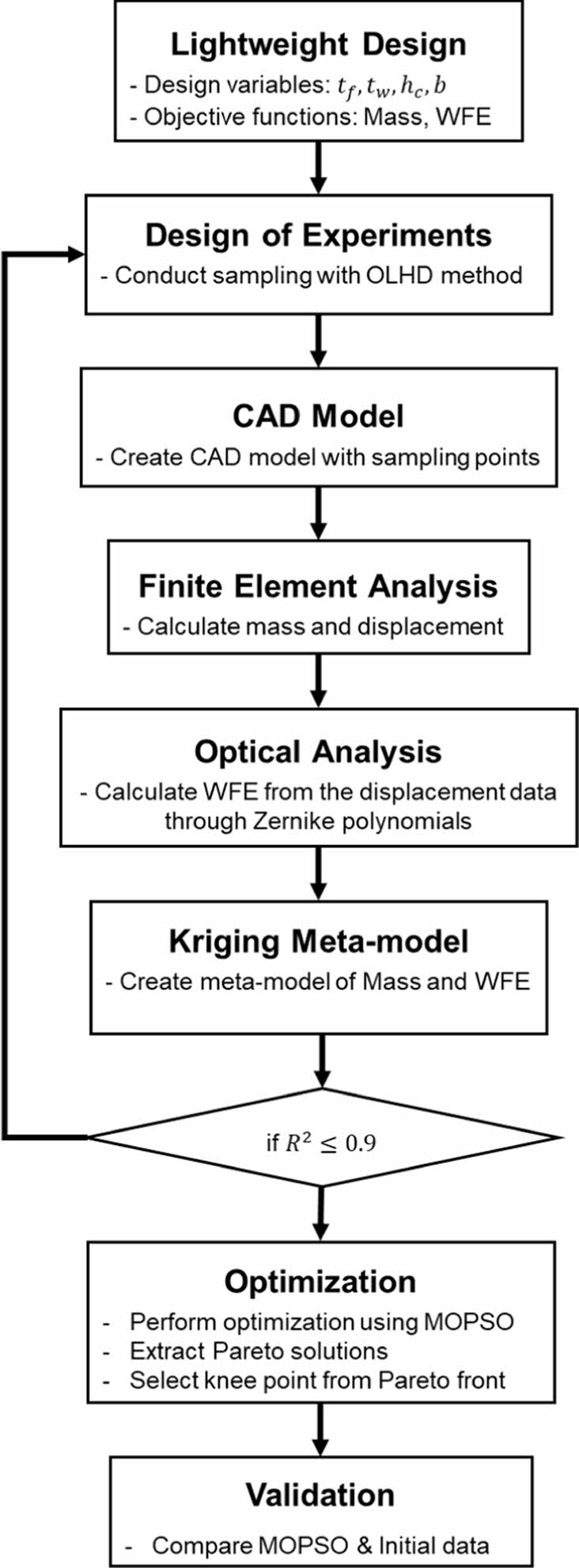
직경 200mm 탄소 섬유 복합재 비구면 반사경의 최적화 과정은 Fig. 6과 같다. 먼저 설계 변수를 정의한 후, 특성 값을 도출하기 위해 최적설계의 정식화를 진행하고 실험계획법을 통하여 실험점을 생성한다. 그 후 크리깅 방법을 사용하여 메타모델을 생성한다. 메타모델의 R² 값이 0.9 이상에 도달하면 MOPSO 알고리즘을 사용하여 파레토 기반의 최적화를 수행하여 최적해를 얻는다.
2.4.1 실험계획법을 이용한 메타 모델 생성
실험계획법에는 직교 배열, 중심 합성 설계(CCD), 라틴 하이퍼큐브 설계(LHD), 그리고 최적 라틴 하이퍼큐브 설계(OLHD)와 같은 다양한 샘플링 방법이 포함된다. LHD는 가장 널리 사용되는 DOE 방법 중 하나이지만, 고유한 무작위성으로 인해 space-filling이 낮을 수 있다. 반면, OLHD는 최적 조건을 포함하여 실험 점들을 균등하게 분포시킴으로써 LHD의 한계를 극복한다. 따라서, 본 연구에서는 정확한 메타모델을 생성하기 위해 OLHD를 선택하였다.
복합재는 일반적인 금속 구조물에 비해 강한 비선형적인 기계적 거동이 발생한다. 따라서 비선형성을 정확히 표현할 수 있는 크리깅 방법을 사용하여 질량과 WFE의 메타 모델을 생성하였다. 질량은 유한요소해석을 통해 계산하였으며, WFE는 Zernike 다항식을 활용하여 분석하였다. 유한요소모델의 표면 변형을 WFE로 해석하기 위해, 패널 표면의 노드 벡터 데이터를 추출한 후, 이를 Zernike 다항식을 사용하여 WFE로 계산하였다[22,23]. 조립 및 정렬 과정에서 해소 가능한 강체 변형을 나타내는 0차부터 2차 항은 제외되었다. 초점 조정 메커니즘이 존재하기 때문에 초점 오차에 해당하는 3차 항도 제외되었다. 따라서 본 연구에서는 광학 성능에 중요한 고차 파면 왜곡을 포착하는 4차부터 24차 항을 활용하였다.
크리깅 메타모델의 정확도를 평가하기 위해 예측 결과를 실제 결과와 비교 검증하는 과정이 필요하다. K-폴드 교차 검증은 오차 분석을 위한 교차 검증 방법 중 하나로, 별도의 검증점을 선택할 필요 없이 이미 얻어진 일부 실험 점들을 사용해 크리깅 메타모델의 정확도를 측정할 수 있는 장점이 있다[24]. 본 연구에는 8개의 검증 점을 사용해 K-폴드 교차 검증을 수행하였다. 검증에는 R² 값을 활용하였으며, 0.90 이상의 R² 값을 허용 가능한 수준으로 간주하였다. 만약 R² 값이 이 임계값보다 낮으면 DOE를 통한 추가 실험이 수행된다. R²의 식은 식 (3)에 제시되어 있다.



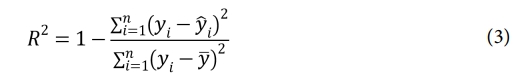
여기서, y_i는 i번째 응답 값, ŷ_i는 i번째 피팅된 응답 값, y̅는 응답 값의 평균을 나타낸다 [25].
2.4.2 Multi-objective particle swarm optimization
MOPSO는 입자군 최적화(Particle swarm optimization, PSO)를 기반으로 실제 산업 현장의 다양한 문제를 효과적으로 해결하기 위해 개발된 알고리즘이다. 자연에서 무리를 이루는 물고기나 새의 행동 양식을 모방한 PSO의 개념을 확장하여, MOPSO는 비지배 솔루션을 저장하는 아카이브(archive), 솔루션을 안내하는 리더(leaders), 그리고 탐색 성능을 높이기 위한 돌연변이(mutation) 연산자를 활용한다. 특히, 파레토 최적해를 활용하여 리더를 선정하며, 다양한 솔루션을 선택해 위치를 업데이트함으로써 솔루션 공간을 더 효과적으로 탐색할 수 있도록 한다[26]. 또한, 크라우딩 거리 방법을 적용하여 해의 다양성을 유지하고, 그리드 메커니즘을 활용한 비지배 솔루션 선택 과정을 통해 파레토 해집합의 적용 범위를 확장한다[27]. 이러한 특성으로 인해 MOPSO는 구현이 쉽고 수렴 속도가 빠르며, 다목적 최적화 문제를 해결하는 데 널리 활용된다.
따라서, 본 연구에서는 질량과 WFE를 동시에 최적화하기 위해 MOPSO 알고리즘을 적용하였다. 입자수는 40으로 설정되었고, 알고리즘은 150번에 걸쳐 반복 수행되었다. MOPSO를 통해 얻어진 파레토 전선에서 가장 효율적인 상충점(trade-off point)을 결정하기 위해 유토피아점에서 거리가 가장 가까운 무릎점(knee point)을 선택하였다. 목표 함수의 단위가 서로 다르기 때문에 유토피아점까지의 최단 거리를 계산하기 위해 정규화를 수행하였다[28].

3.1 최적화 결과
비구면 반사경 제작에 사용된 AS4/3501-6 UD 복합재의 기계적 물성치는 Table 2에 나타나 있다.
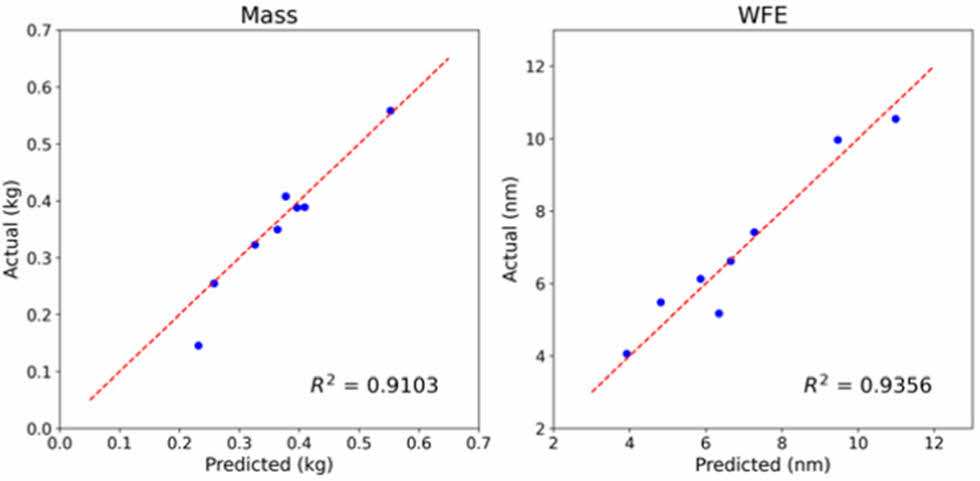
실험계획법을 통해 설계 변수 범위 내에서 직경 200mm 탄소 섬유 복합재 비구면 반사경에 대해 31개의 실험점이 생성되었다. 각 실험점 데이터로 FEA를 수행하여 질량과 WFE 값을 계산하였으며, 이는 Table 3에 제시되어 있다. 이러한 값을 기반으로 질량과 WFE에 대한 크리깅 메타모델이 생성되었다. Fig. 7에 나타난 바와 같이, 질량과 WFE의 R² 값은 각각 0.9103과 0.9356로, 두 값 모두 0.9 이상을 보여 메타모델의 정확도가 허용 가능한 수준임을 확인하였다.
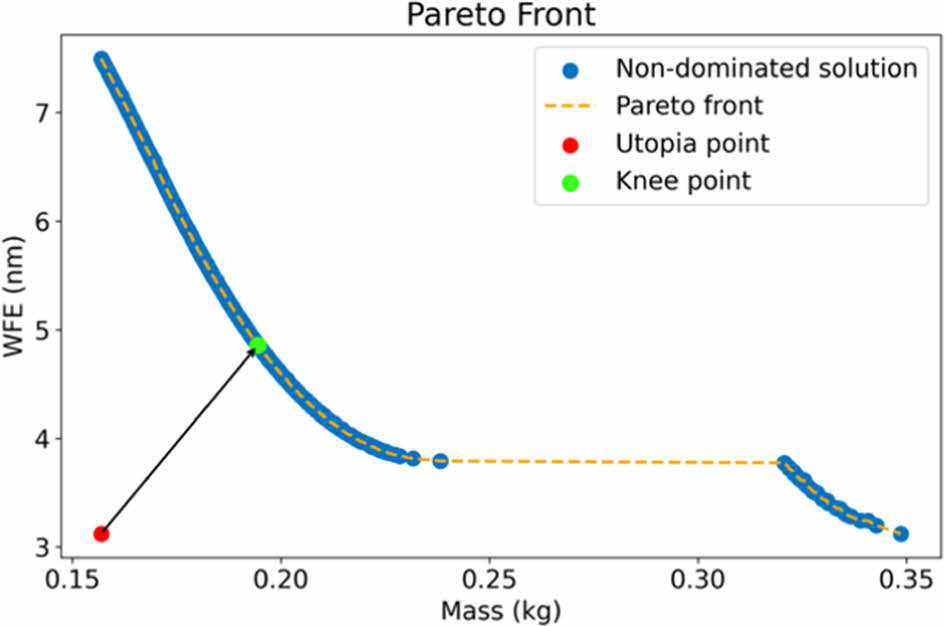
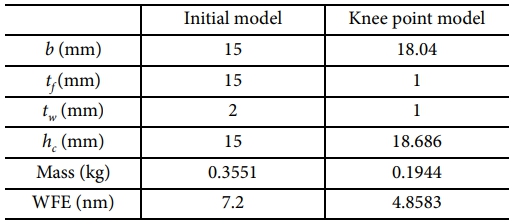
최적화는 MOPSO를 사용하여 질량과 WFE를 동시에 최소화하기 위해 파레토 프론트를 도출하는 방식으로 수행되었다. 결과를 정규화하여 유토피아 점에 가장 가까운 무릎점을 도출하였으며, 이는 Fig. 8과 Table 4에 나타나 있다.
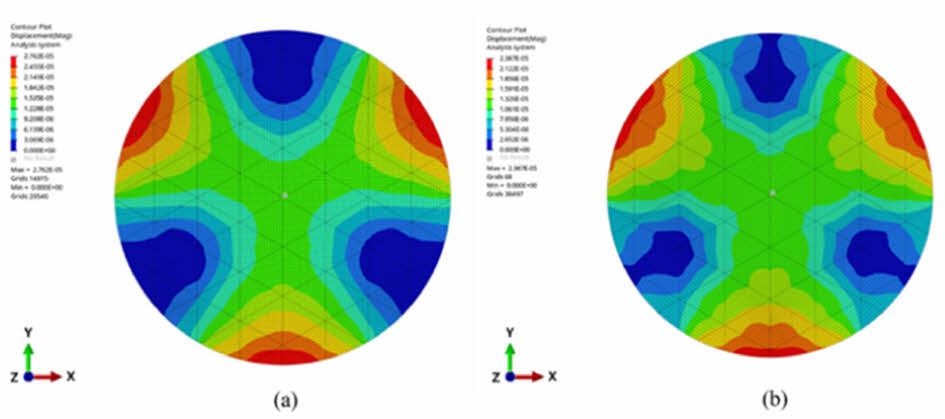
MOPSO 알고리즘으로 부터 얻은 무릎점 데이터를 검증하기 위해, 해당 설계 변수를 이용하여 유한요소해석 무릎점 모델을 생성하였다. 1G 중력 하에서 초기 모델과 무릎점 모델의 패널 Z축 변위를 비교하였다. Fig. 9에서 볼 수 있듯이, 무릎점 모델은 초기 모델보다 변위가 감소하는 모습을 보였으며, 이는 WFE에도 영향을 미칠 것으로 예상된다.
Table 4는 위의 초기 모델과 무릎점 모델의 비교 결과를 나타내며, 무릎점 모델이 초기 모델과 비교하여 질량과 WFE를 모두 감소시키는 데 성공했음을 보여준다. 구체적으로, 질량은 약 45.3% 감소하였으며, WFE는 약 32.5% 감소하였다. 설계 변수의 경우, 반사경의 직경을 유지하면서 질량을 줄이기 위해 그리드와 패널의 두께는 얇아지고, 반사경의 높이와 그리드 내접원 직경이 증가하는 방향으로 최적화된 것으로 판단된다.

본 연구는 다목적 최적화를 통해 탄소 섬유 복합재 비구면 반사경의 WFE를 줄임과 동시에 경량화를 달성하였다. 계산 비용을 줄이기 위해 실험계획법을 사용하여 크리깅 메타모델을 생성하였으며, 교차 검증을 통해 메타모델의 정확도를 검증하였다. MOPSO 알고리즘을 활용하여 다중 목적 최적화를 진행하였고, 파레토 전선상의 무릎점 데이터로 최적 모델을 도출하였다. 최적 설계 결과, 초기 모델 대비 질량은 약 45.3%, WFE는 약 32.5% 감소하였으며, 이는 제안된 최적화 방법이 고성능 탄소 섬유 복합재 비구면 반사경 설계에 효과적으로 기여함을 나타낸다.
제안된 최적화 기반 설계 방법은 직경 150–500 mm 범위의 항공용 EO/IR 시스템용 반사경을 대상으로 하며, 해당 범위 내에서 실효성 있게 적용 가능함을 검증하였다. 반사경의 크기가 증가할 경우 자중(self-weight) 및 외부 하중에 의한 구조적 안정성과 누적 열팽창으로 인한 열변형 영향이 커질 수 있으나, 설계 변수 범위 조정, 복합재료의 적층각 및 라미네이트 두께 조절을 통해 충분히 대응 가능하다.
특히, 연구에서 사용된 설계 변수들은 모두 반사경의 질량에 영향을 받는 변수이므로, 반사경의 크기가 달라지더라도 동일한 설계 변수와 최적화 방법을 적용할 수 있다는 장점이 있다. 나아가, 제안된 최적화 방법은 향후 특정 작동 환경 및 탑재체에 요구 사항에 맞추어 특정 파장 범위 또는 기타 광학적 요구 조건을 고려한 성능 최적화로 확장될 수 있다. 이는 차세대 초경량 고정밀 반사경 설계에 중요한 기여를 할 것으로 기대된다.

본 연구는 한화시스템(주)의 지원을 받아 수행된 연구임(2022R1AC2011034).