This study analyzes the effect of the stacking sequence of a carbon fiber reinforced polymer (CFRP) pressure vessel cylinder on impact damage and residual burst pressure. To achieve this, finite element analysis (FEA) incorporating a continuum damage mechanics (CDM)-based damage model was conducted to evaluate the impact behavior, damage patterns, and burst pressure of the cylinder under different impact energy levels. The results indicate that the impact behavior and damage characteristics vary significantly depending on the stacking sequence of the composite material. Under a 30 J impact, the BM’s residual burst pressure dropped from 34.6 MPa to 24.2 MPa (-30.1%), whereas the cross-ply models M1 and M4 fell only to 30.2 MPa (-12.5%) and 33.2 MPa (-3.5%), respectively. When hoop and helical layers are alternately stacked, delamination damage increases internally. However, the dispersion of impact energy effectively suppresses fiber damage in the hoop layers, preventing a significant reduction in burst pressure.

본 연구에서는 탄소섬유 강화 복합재료(Carbon Fiber Reinforced Polymer, CFRP) 압력용기 실린더의 적층 순서가 충격 손상 및 잔류 파열압력에 미치는 영향을 분석하였다. 이를 위해 연속체 손상역학(Continuum Damage Mechanics, CDM) 기반의 손상 모델을 적용한 유한요소해석(Finite Element Analysis, FEA)을 수행하여, 충격 에너지에 따른 실린더의 충격 거동, 손상 양상 및 파열압력을 평가하였다. 분석 결과, 적층 순서 변화만으로도 충격 거동과 손상 양상이 크게 달라졌다. 30 J 충격 시 BM의 경우 잔류 파열압력이 34.6 MPa에서 24.2 MPa로 30.1% 감소한 반면, 교차 적층(M1, M4) 모델의 경우 각각 30.2 MPa(-12.5%)와 33.2 MPa(-3.5%)로 저하폭이 현저히 줄었다. 이는 후프층과 헬리컬층을 교차 배치할 경우 층간 분리가 다소 늘어나더라도 후프층 섬유 손상이 억제되어 파열압력의 급격한 저하는 방지되는 것을 확인하였다.

Keywords: 탄소섬유 강화 복합재료(Carbon fiber reinforced polymer, CFRP), 복합재료 압력용기(Composite pressure vessel), 충격 손상(Impact damage), 파열압력(Burst pressure), 적층 순서(Stacking sequence)

전 세계적인 탄소중립 정책 강화로 인해 무탄소 및 저탄소 에너지원인 수소의 수요가 꾸준히 늘고 있다. 이에 따라 고압 상태에서 수소를 안정적으로 저장 및 이송하기 위한 핵심 장비로 탄소섬유 강화 복합재료(CFRP) 압력용기가 각광받고 있다[1,2]. CFRP는 높은 비강도와 비강성을 갖추어 금속 용기에 비해 무게를 크게 줄이면서도 충분한 내압 성능을 확보할 수 있다는 장점을 지닌다. 대표적으로 내부 고분자 라이너를 CFRP로 감싸 제작한 Type IV 복합재료 압력용기가 상용화 단계에 접어들어 수소 연료를 사용하는 다양한 산업 분야에서 활용 폭을 넓혀가고 있다[3-5].
그러나 CFRP가 지닌 낮은 파괴인성으로 인해 외부 충격에 취약하다는 문제점이 꾸준히 제기되고 있다. 용기의 제작 및 수소의 운송, 취급 과정에서 용기에 저속 충격이 가해지면 섬유파손, 층간분리, 기지파손 등이 복합적으로 발생해 압력용기의 파열압력이 낮아져 내압 성능이 급격히 저하될 수 있다[6-9]. 특히, 압력용기 실린더의 경우 후프층(hoop layer)이 대부분의 하중을 담당하므로 후프층의 섬유파손은 내압 성능을 심각하게 저하시킬 수 있다[10,11]. 따라서 충격 하중을 효과적으로 완화해 손상을 줄이는 설계 기법이 요구되며, 이를 위해서는 충격 손상 메커니즘과 손상이 내압 성능에 미치는 영향을 면밀히 분석하여 설계에 고려할 필요가 있다.
최근에는 충격 손상이 복합재료 압력용기의 내압 성능에 미치는 영향을 체계적으로 분석하기 위해 실험적 접근과 수치해석을 병행하는 연구가 활발히 이루어지고 있다[12,13]. 특히, 해석적 연구에서는 효율적인 손상해석이 가능한 연속체 손상역학(continuum damage mechanics, CDM) 기반의 점진적 손상해석 기법이 주로 사용되고 있다[14-17]. 이를 통해 손상이 구조의 잔류강성과 강도에 미치는 영향을 분석하고 충격 손상을 완화하기 위한 연구가 점차 확대되고 있다. 하지만 압력용기의 설계변수에 따른 충격 손상과 잔류 파열압력을 체계적으로 분석한 연구는 부족한 실정이다.
본 연구에서는 압력용기 실린더의 적층 순서가 충격거동, 충격 손상 및 잔류 파열압력에 미치는 영향을 분석하고자 한다. 이를 위해 복합재료의 대표적인 손상인 섬유파손, 기지파손, 층간분리 손상을 고려할 수 있는 유한요소해석모델을 구축하였으며, 다양한 충격 에너지 및 적층 패턴에 따른 충격손상과 잔류 파열압력을 체계적으로 비교 분석하였다.

2.1 연속체 손상역학 접근법
유한요소해석은 연속체 손상역학 기반 손상모델을 이용하였으며, ABAQUS/Explicit을 활용해 복합재료 압력용기의 충격 및 파열압력 해석을 수행하였다. 복합재료의 대표 손상모드 중 섬유파손과 기지파손은 ABAQUS 사용자 정의 재료 모델 VUMAT으로 구현된 Kim[16]의 모델을 사용하였으며, 층간분리 손상은 CZM 모델을 적용한 고려하였다.
연속체 손상역학 접근법에서 재료의 손상 효과는 내부 손상을 균질화해 재료 물성을 저하시키는 방식으로 표현되며, 식 (1)과 같은 degradation 계수에 의해 재료 물성이 감소된다고 가정한다.



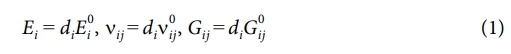
여기서 d_i(=1 - ω_i)는 degradation 계수이며, E_i ν_ij G_ij는 각각 탄성계수, 포와송 비, 전단계수를 나타낸다. 윗첨자 0는 손상이 나타나기 전 초기 물성값을 의미하며, w_i는 손상변수로 복합재료의 손상 진전 정도를 결정한다. 섬유파손과 기지파손을 위한 손상변수는 강도의 확률분포(와이블(Weibull)분포)를 기반으로 모델링 되며, 1차원 응력-변형률 관계에서는 식 (2)와 같이 나타낼 수 있다.



여기서, m은 와이블 분포의 shape parameter이며, ε_f 는 파손 변형률을 의미한다.
2.2 층내 손상(intra-laminar damage) 모델
복합재료의 손상을 정밀하게 구현하기 위해서는 크게 두 가지 조건을 설정해야 한다. 첫번째로 복합재료의 초기 손상을 판단하는 손상기준이 설정되어야 하며, 두번째는 손상의 진전을 구현하기 위한 손상진전법칙을 적용해야 한다. 본 연구에서는 충격하중에 의해 발생하는 복합재료의 두께방향 응력도 함께 고려하기 위해 3차원 요소(C3D8R)를 사용하였으며, 이를 위해 대표적인 손상기준의 하나인 Hashin failure criteria[18]와 maximum stress criteria를 적용하였다. 이 손상기준은 손상모델과 함께 각 요소에서 세 방향의 인장-압축과 전단 손상을 고려하는데 활용된다.
2.3 층간분리 손상(inter-laminar damage) 모델
복합재료의 층간분리 손상을 고려하기 위해서 응집영역모델(cohesive zone model)을 적용하였으며, ABAQUS에서 제공하는 응집요소(cohesive element)를 사용하였다[19]. 응집요소는 거의 무시할 수 있을 정도의 두께로 접합되어 있는 두 구조물 사이의 계면층을 나타낼 수 있도록 개발되었으며, 두께가 아주 얇기 때문에 응력-변형률 관계 대신 힘-변위 관계로 정의된다. 초기 손상 판정을 위한 손상기준은 응력기반의 Quadratic nominal stress criteria를 사용하였고, 손상의 진화방정식은 Benzeggagh–Kenane(B-K)식을 사용하였다.

3.1 복합재료 압력용기 해석 모델
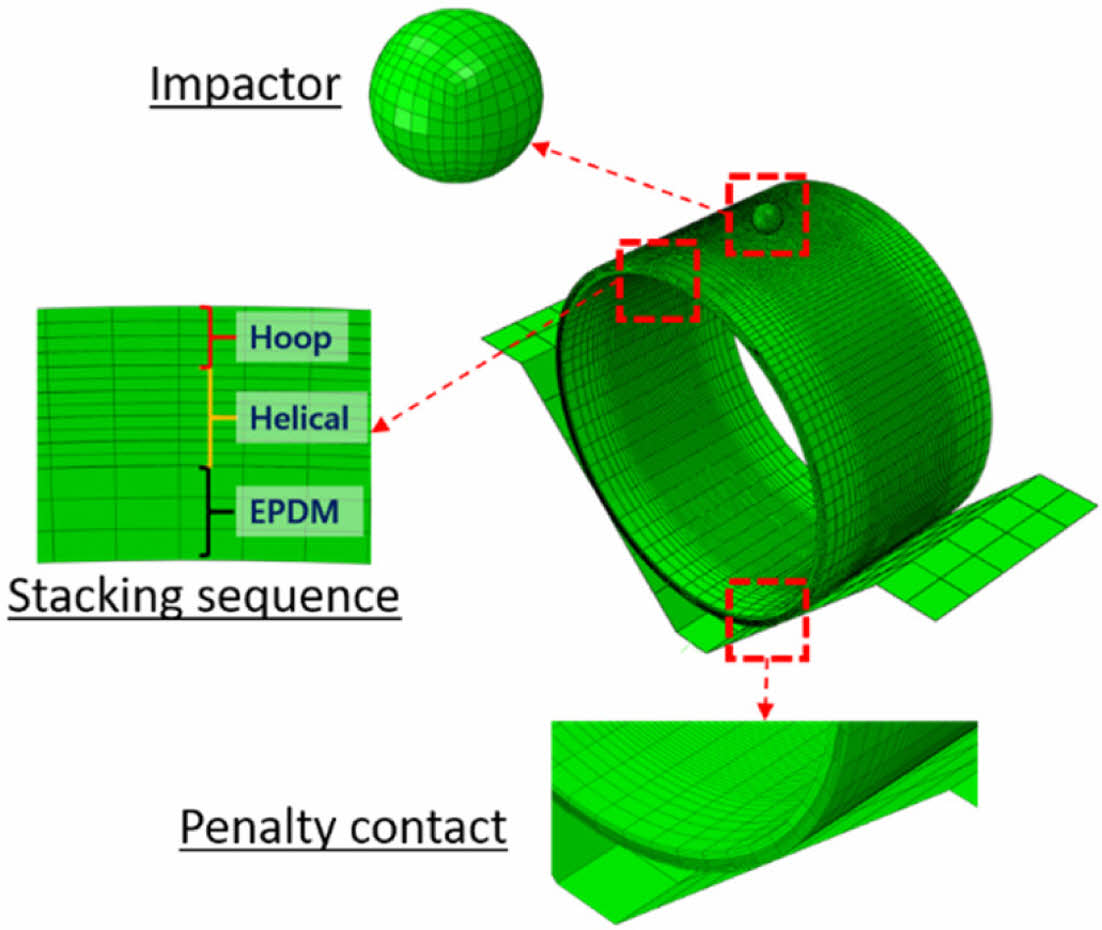
복합재료 압력용기 해석모델은 Kim et al.[15]의 실험시편 모델을 바탕으로 개발하였으며, Fig. 1과 같이 압력용기의 실린더 부분으로 고분자 라이너(Ethylene Propylene Diene Monomer, EPDM) 위에 CFRP가 적층되어 있다. 시험편의 적층 순서는 [(90°)₄/(20°/-20°)₄/EPDM]_T 이며, 후프층과 헬리컬층(helical layer), 라이너의 두께는 각각 1.1 mm, 1.9 mm, 1.8 mm이다. 압력용기 모델의 적층 순서는 시험편과 동일하게 [(90°/c)₄/(20°/-20°/c)₄/EPDM]_T 로 구성하였고, 여기서 c는 cohesive 요소(COH3D8)층을 의미하며, 층간분리 손상을 고려하기 위해 삽입되었다. 압력용기 모델은 내경 157mm, 축 방향 길이 100 mm로 구성하였다. 충격해석 모델은 복합재료 압력용기 실린더와 steel 충격자(구 직경 12.7 mm), V형 지지대로 이루어져 있다. 압력용기의 CFRP 층과 EPDM 라이너, 충격자는 모두 ABAQUS의 3차원 6면체 요소인 C3D8R로 모델링하였으며, V형 지지대는 강체로 모델링 하였다. 복합재료 압력용기와 충격자 사이, 복합재료 압력용기와 V형 지지대 사이에는 접촉 조건으로 penalty contact을 부여하였다. 충격이 가해지는 중심 영역에는 비교적 크기가 작은 메쉬를 적용하였고, 나머지 영역에는 해석의 효율성을 위해 상대적으로 더 큰 메쉬를 사용하였다.
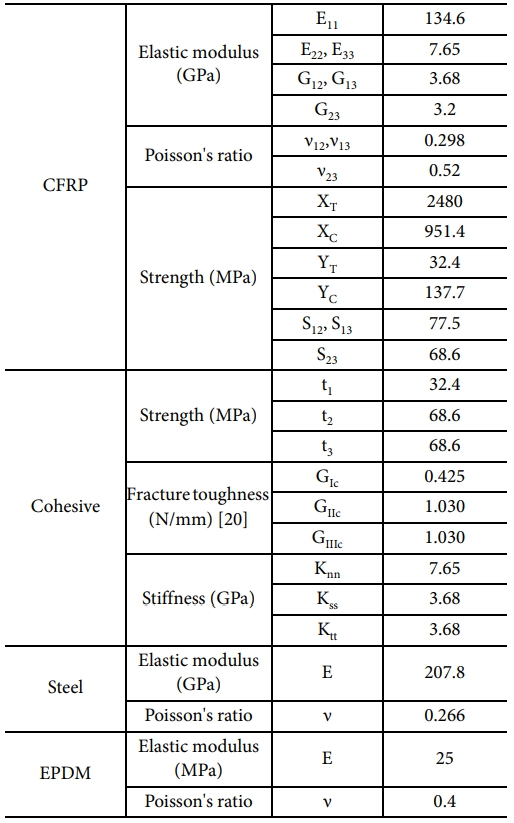
해석 모델에 사용한 CFRP 물성은 Kim[15]이 T700/Epon826 단일방향 시험편 30개에 대해 ASTM D3039, D3410, D5379, D2344 시험을 수행하여 제시한 탄성계수 및 강도계수 데이터를 사용하였다. Mode I cohesive 강도는 CFRP의 인장강도 Y_T를, Mode II, III cohesive 강도는 CFRP의 전단강도 S₂₃ 와 같다고 가정하였으며 층내 파괴인성의 경우 사전연구[20]의 값을 인용하였다. 본 연구에서 사용한 재료 물성은 Table 1에 나타나 있다.
3.2 적층 순서 변경 모델
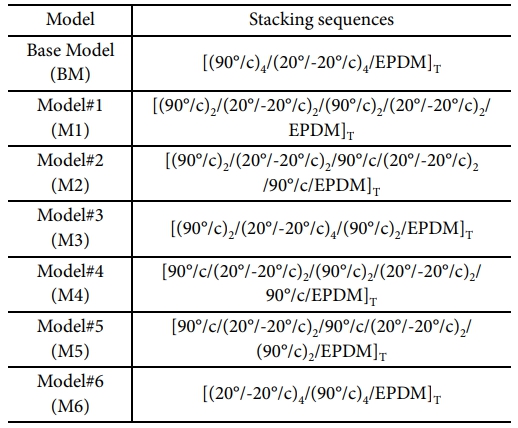
기존 해석 모델(Base Model(BM))에서 후프층과 헬리컬층의 적층 순서를 다르게 한 Model#1~Model#6 모델을 설계하고, 각 모델에 대해 충격해석 및 파열압력 해석을 수행하였다. Table 2는 각 해석 모델의 적층 순서를 보여준다. 해석 모델의 적층 순서는 적층 구조에 따른 복합재료 압력용기의 파열압력을 선행 연구한 문헌[21]을 바탕으로 결정하였다.
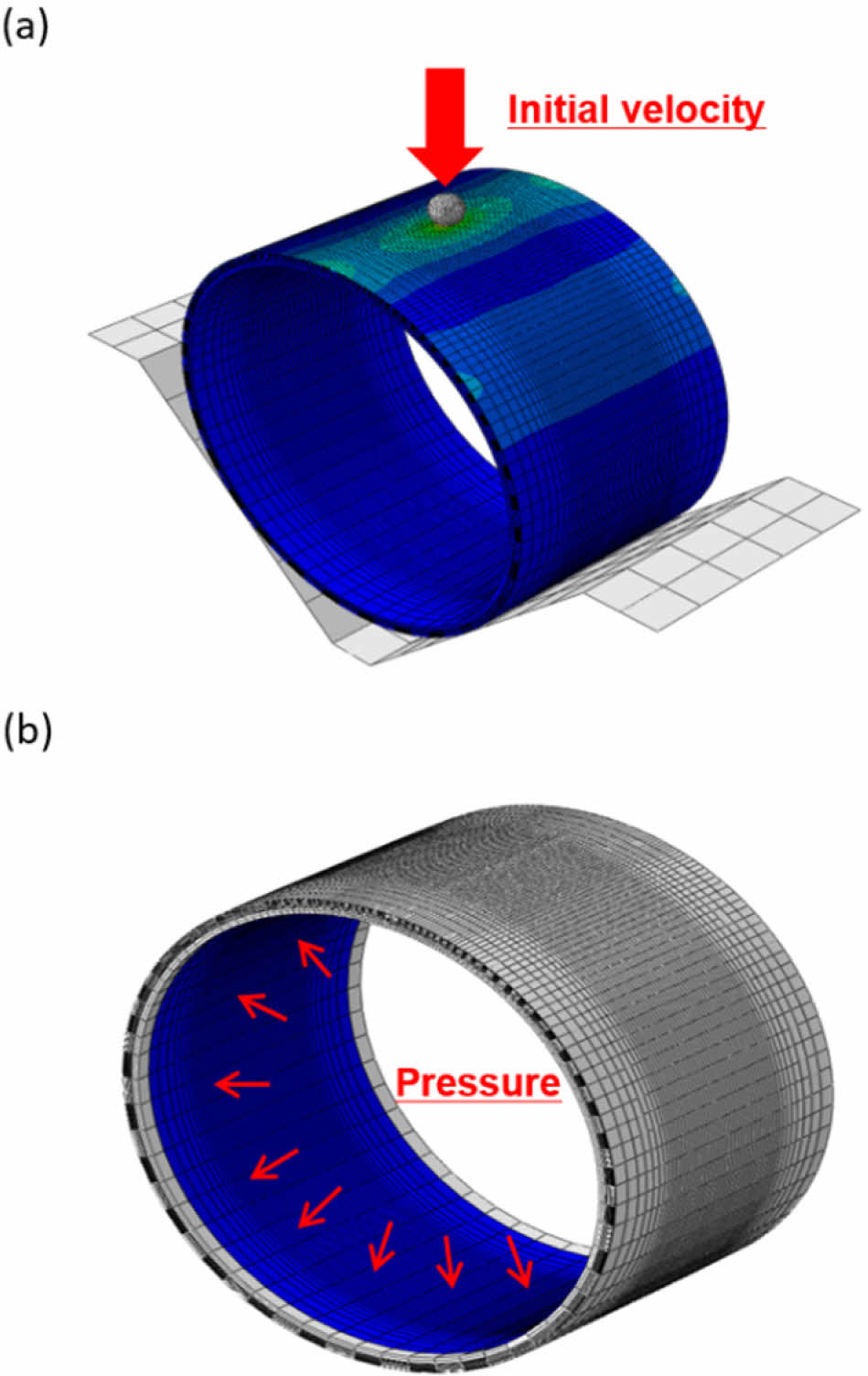
Fig. 2는 충격해석과 파열압력 해석에 적용한 유한요소 모델 및 해석 절차를 보여준다. 충격해석의 경우 충격자에 초기속도를 부여해 V형 지지대 위의 압력용기에 낙하되는 충격해석 과정을 보여주며 10 J, 20 J, 30 J 총 3가지 에너지 조건에서 해석을 수행하였다(Fig. 2a). 또한, 용기에 발생한 충격 손상이 용기의 파열압력에 미치는 영향을 분석하기 위해 낙하충격으로 손상된 상태를 반영하여 파열압력 해석을 수행하였으며, 실린더 내부 라이너에 용기가 폭발할 때까지 압력을 부여하는 방식으로 진행하였다(Fig. 2b).

4.1 복합재료 압력용기 해석 모델 검증
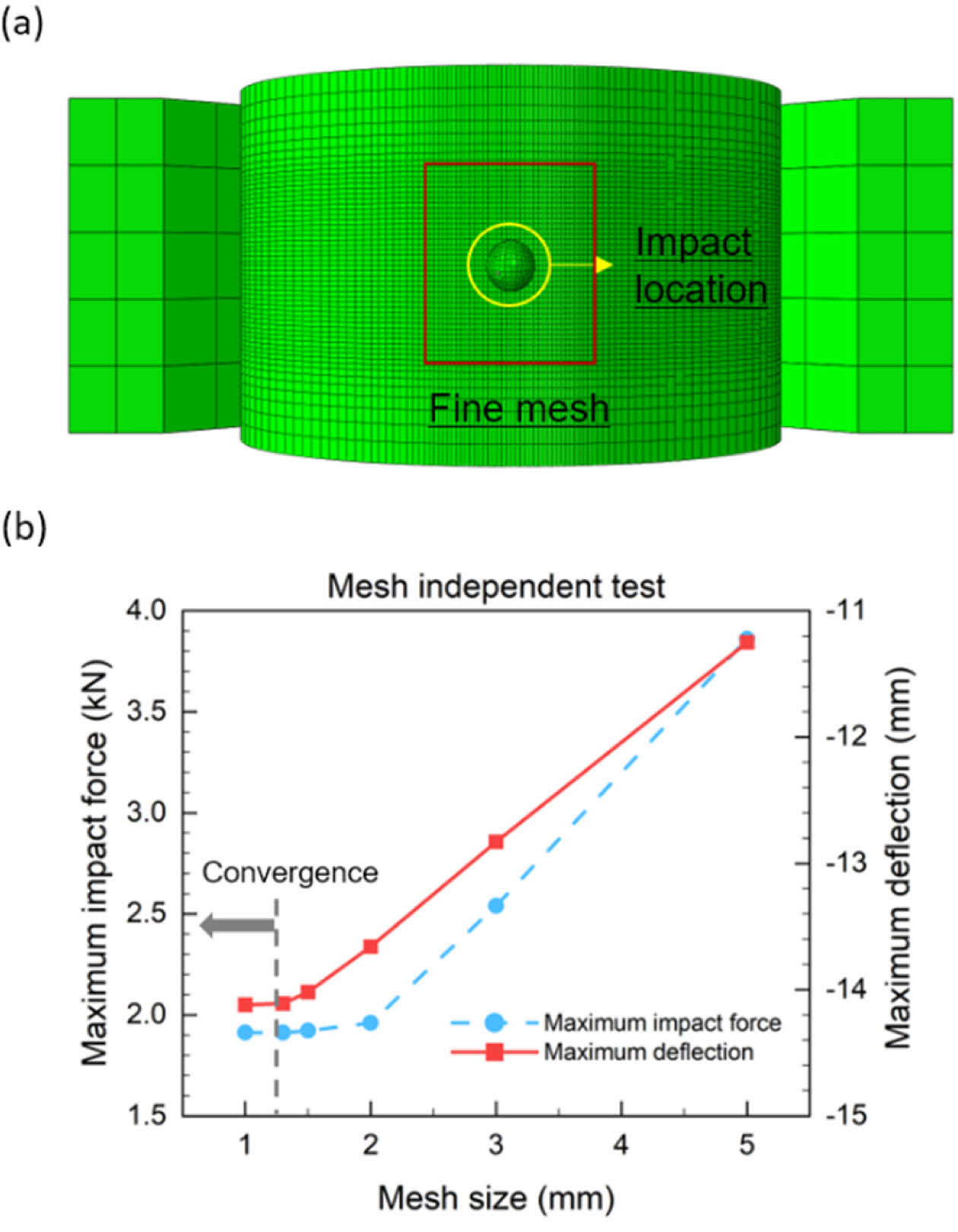
충격해석 및 파열압력 해석의 정확도와 효율성을 높이기 위해 메쉬 수렴 테스트를 실시하여 압력용기의 메쉬 크기를 결정하였다. 충격이 가해지는 중심부에는 상대적으로 촘촘한 메쉬(fine mesh)를, 나머지 영역에는 좀 더 큰 메쉬(coarse mesh)를 사용하였으며, 중심부 메쉬 크기에 따른 최대 충격력 및 최대 처짐량을 비교하였다(Fig. 3a). 5 mm부터 1 mm까지, 총 6단계로 메쉬 크기를 줄여가며 충격해석을 수행한 결과, 중심부 메쉬 크기가 1.3 mm일 때 최대 충격력 및 최대 처짐량이 수렴함을 확인하였다(Fig. 3b). 이에 따라 해석 모델에서 중심 영역의 메쉬 크기를 1.3 mm로 고정하여 최종 해석에 활용하였다.
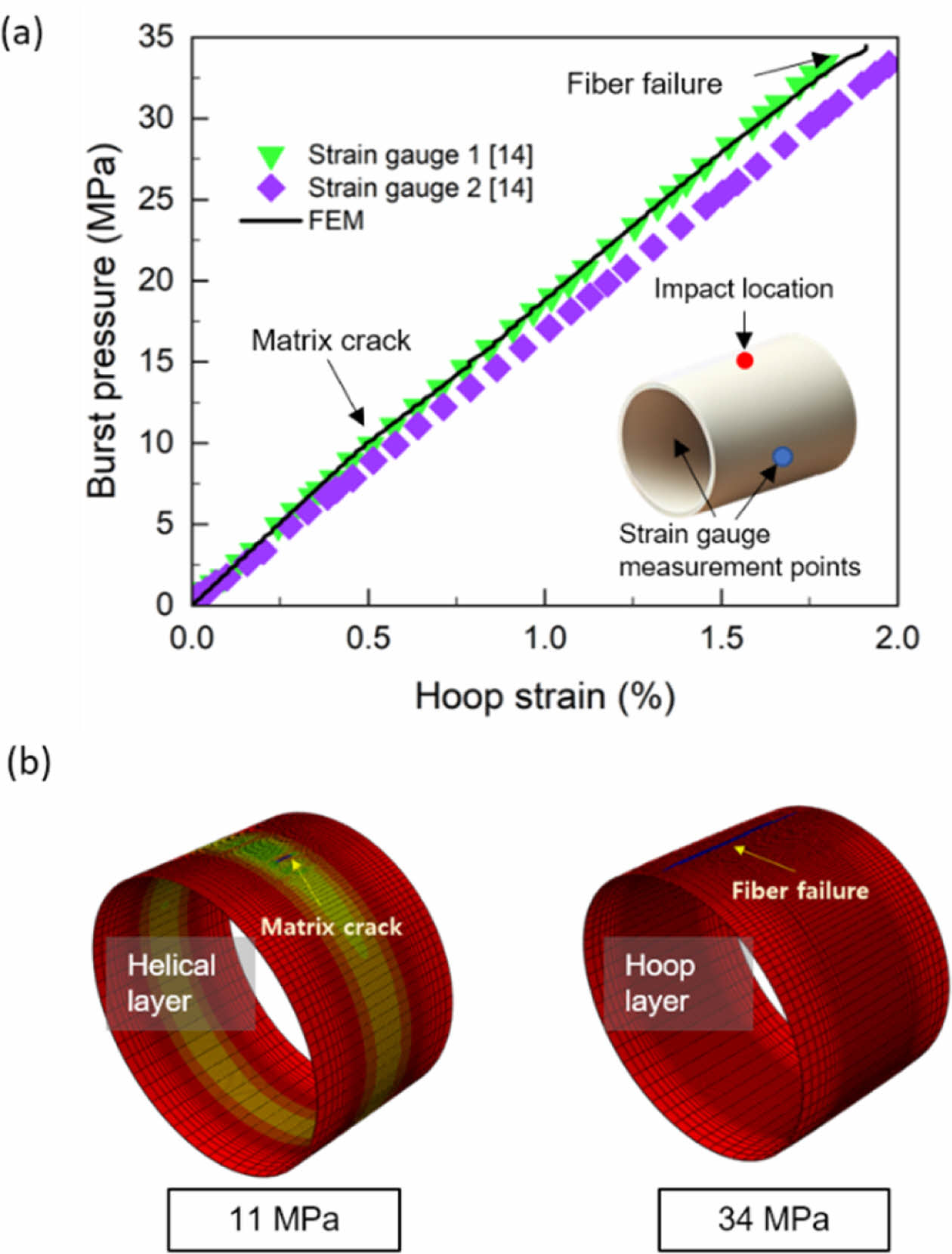
적층 패턴에 따른 영향을 분석하기 전, 해석 모델 검증을 위해 시험편과 동일한 적층 형태를 갖는 Base모델을 사용하여 충격손상이 없는 상태로 파열압력 해석을 수행해 압력에 대한 hoop 방향 변형율을 실험 값[14]과 비교하였다. Fig. 4a는 실험과 해석에 나타난 파열압력 결과를 보여준다. 해석 모델의 파열압력은 실험 결과와 대체로 일치하는 것을 확인하였다. 해석 결과에서 용기의 내부 압력이 약 11 MPa 부근에 도달하면 헬리컬층에서 기지파손이 발생했으며, 약 34 MPa 부근에서 후프층에 섬유파손이 나타나면서 손상으로 인해 용기가 폭발하였다(Fig. 4b). 이는 복합재료 압력용기의 파열압력은 후프층이 주로 지탱하며, 그만큼 후프층의 손상을 줄이는 것이 파열압력을 안정적으로 유지하는데 중요한 요소임을 시사한다.
4.2적층순서에따른충격거동및손상비교
복합재료 압력용기의 적층 순서가 충격 손상에 미치는 영향을 확인하기 위해 각 모델에 대해 충격 에너지를 10 J, 20 J, 30 J로 달리 적용하여 충격해석을 수행하고 그에 따른 충격거동 및 손상을 비교분석 하였다. Base 모델(BM)과 M6, M2~M5 모델은 유사한 충격거동이 나타나는 것으로 확인되었다. 해석결과 분석을 위해 유사한 거동을 보인 모델에서 대표모델을 선정하여 분석하였다. BM와 M6 중에서는 BM을, M2~M5 중에서는 M4를 선택하였다. 유사한 거동을 보이지 않은 M1 역시 함께 비교분석 하여 총 3가지 모델에 나타난 충격거동 및 손상을 정밀하게 비교분석 하였다.
압력용기에 나타난 손상 모드는 섬유손상, 기자파손, 층간분리 3가지를 비교하였으며, 이중 상대적으로 큰 강도 저하를 유발하는 섬유파손과 층간분리 손상을 집중적으로 분석하였다. 섬유손상 및 기지파손의 경우 손상 발생 후 degradation factor를 적용하여 재료 물성을 축소 하는 방식으로 손상을 판단하였으며, 수치적 오류를 방지하기 위해 0.01로 제한하였다(0.01≤D_FAC(di)≤1). 층간분리 손상의 경우 손상이 발생하면 파괴변수가 증가하며 D≥0.95일 때 실질적 delamination이 발생한 것으로 판단하였다.
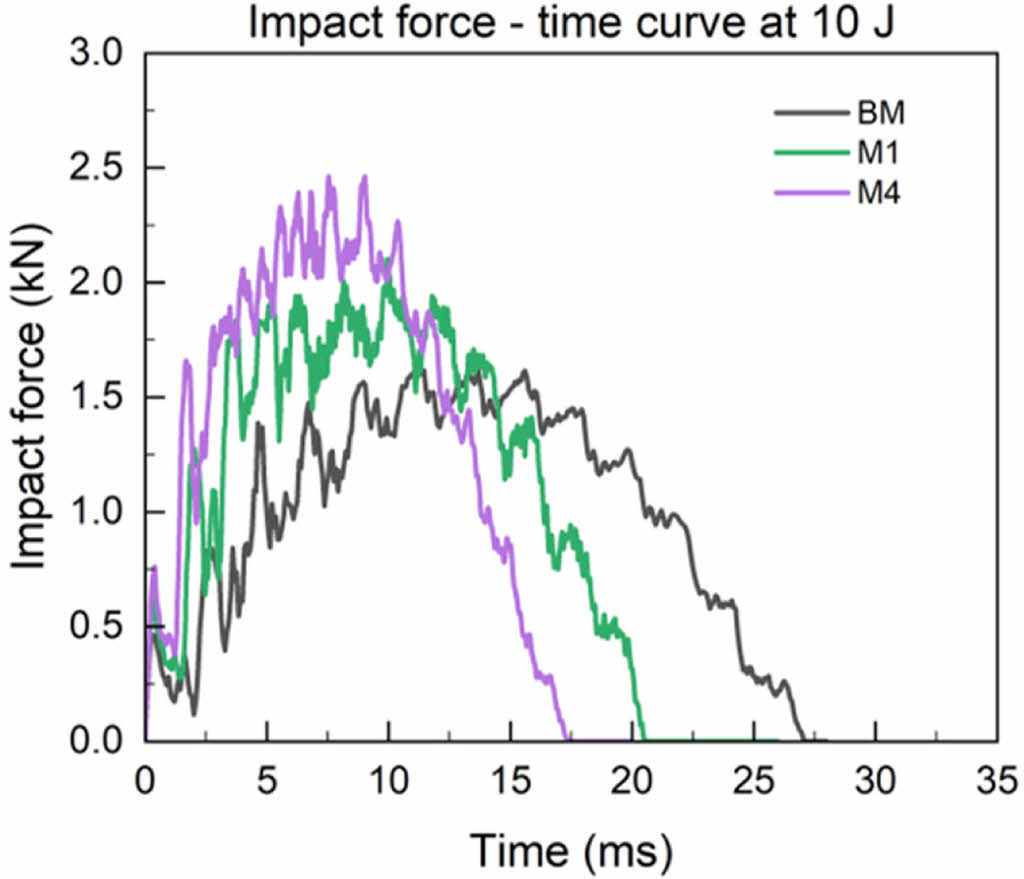
Fig. 5a는 충격 에너지 10 J에서 세 가지 모델에 나타난 충격거동을 보여준다. BM의 경우 M1과 M4 모델과 비교하였을 때 상대적으로 낮은 충격력을 보였으며, 충격자와 용기의 접촉 시간은 가장 긴 것으로 나타났다. 이는 BM이 M1과 M4에 비해 상대적으로 손상이 더 크게 나타나서 발생하였다.
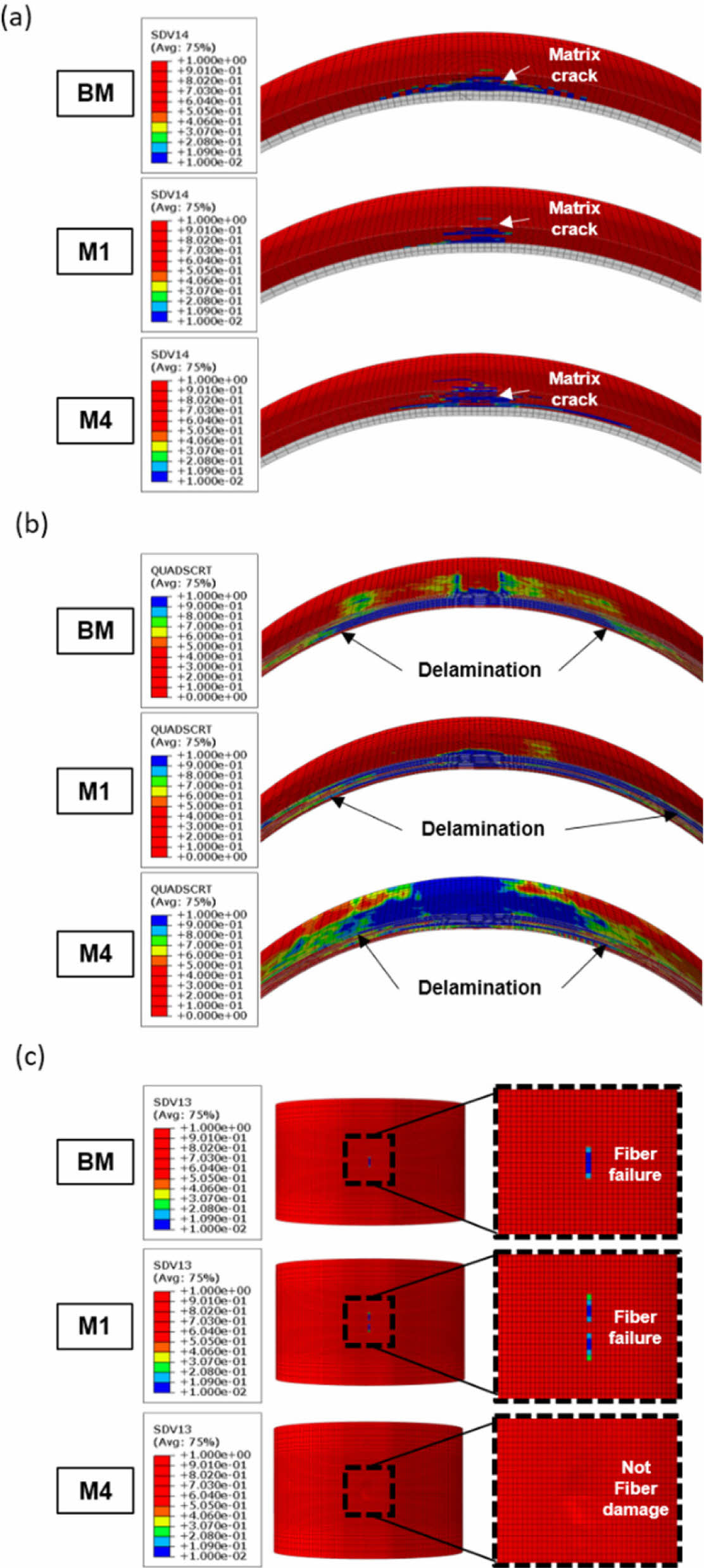
Fig. 6은 충격 에너지 10 J에서 BM과 M1, M4에 발생한 충격 손상을 보여준다. 먼저 기지파손을 살펴보면, BM은 라이너(Liner) 가까운 헬리컬층에서 기지파손이 넓게 분포하였으나 외부 표면에는 손상이 관찰되지 않았다(Fig. 6a). M1 역시 모든 헬리컬층에 기지파손이 발생하였으며, BM과 마찬가지로 외부 표면에서는 손상이 나타나지 않았다. 그러나 M4는 헬리컬층뿐 아니라 실린더 외부 표면에서도 기지파손이 발생하여 적층 패턴에 따른 외부 표면 파손 특성이 뚜렷하게 드러났다. Fig. 6b는 동일 조건(10 J)에서 확인된 층간분리 손상 영역을 보여준다. BM은 라이너 인접부에서 층간분리가 크게 진전되었고, 후프층이 적층된 상부 영역에서는 상대적으로 작은 손상만 관찰되었다. 그러나 후프층과 헬리컬층을 교차 적층한 M1과 M4는 후프층과 헬리컬층 사이 계면이 여러 층으로 형성되어 있어 BM에 비해 층간분리 범위가 더 크게 나타나는 경향을 보였다. Fig. 6c는 후프층에서 발생한 섬유파손을 나타낸다. 10 J 충격 조건에서, BM은 후프층에 섬유파손이 관찰되었으나 M1은 섬유손상이 제한적으로 발생하였다. M4의 경우 헬리컬층 및 외부 표면 기지파손은 크게 나타났으나, 후프층 섬유손상은 관찰되지 않았다.
결과적으로 BM 모델의 경우 섬유파손, 기지파손, 층간분리가 모두 관찰되었으며, M1, M4에 비해 상대적으로 크게 진전되었다.
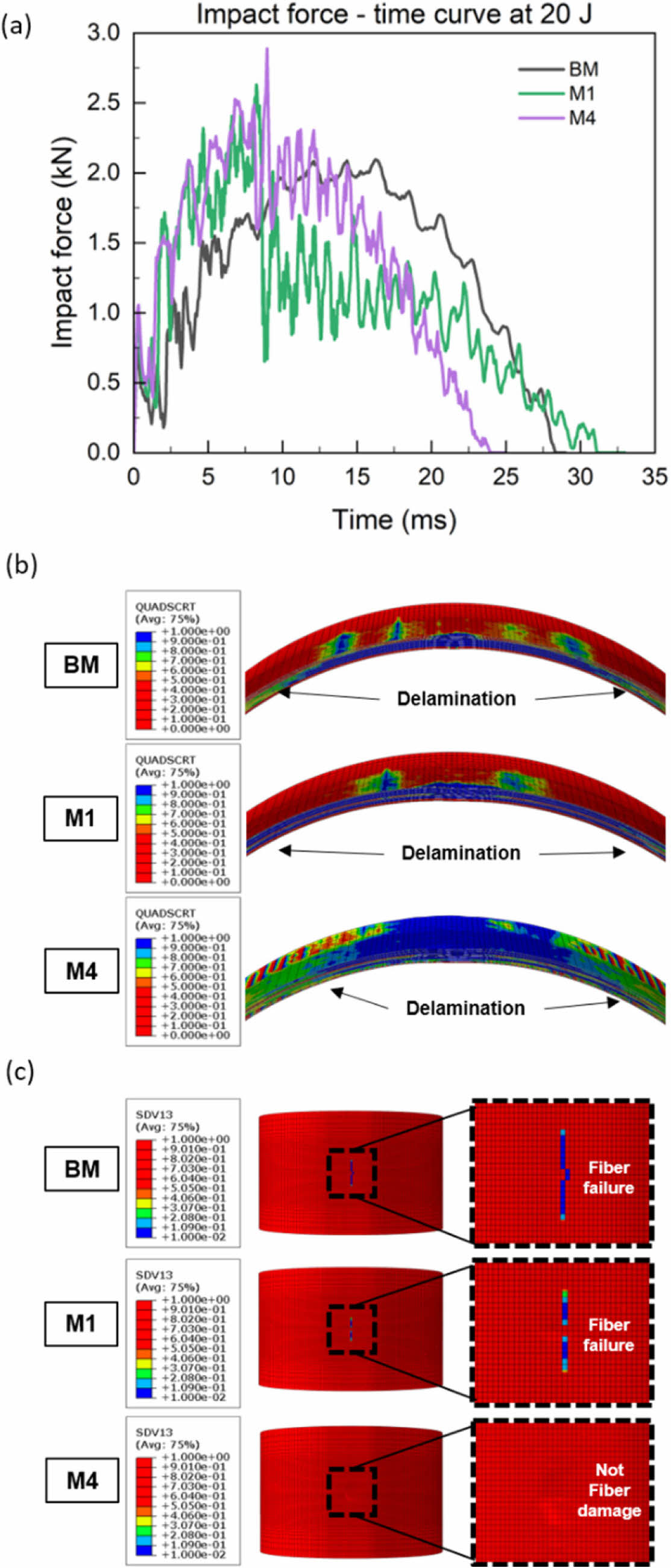
Fig. 7a는 충격 에너지 20 J에서 각 모델에 나타난 충격거동을 나타낸다. M1과 M4의 경우 9 ms에서 상대적으로 큰 충격력 저하가 나타났다. 이는 층간분리 손상이 급격히 증가하는 시점에 발생한 것으로 확인되었으며, 층간분리 손상이 급격히 확장되면 실린더의 굽힘 강성이 급격히 저하되어 충격력이 크게 저하되는 것으로 판단된다(Fig. 6b). 일반적으로, 섬유강화 적층 복합재료에서 굽힘 변형이 나타나면 섬유 방향이 다른 인접한 층에서 응력의 차이로 인해 층간분리가 발생하며, 특히, 충격의 경우에는 이와 함께 기지파손이 전파되면서 섬유의 방향이 상이한 층을 만나면 층간분리로 크랙의 방향이 전환되며 더 쉽게 층간분리가 발생할 수 있다[11]. 따라서 후프층과 헬리컬층을 교차하여 적층하면 후프층과 헬리컬층 사이 계면 영역에서 층간분리가 크게 발생하게 된다. M1과 M4의 경우 후프층과 헬리컬층이 교차 적층되어 다층 층간분리가 발생하였으며, BM에 비해 층간분리가 더 크게 진전되었다. 그러나 두 모델 모두 후프층에서 발생한 섬유손상의 경우 충격 에너지가 증가하였음에도 10 J에서 발생한 손상과 비슷하게 나타났으며 진전되지 않았다 (Fig. 6c). 이는 층간분리에 의해 층이 나누어 지면, 굽힘강성이 저하되어 변형은 더 커질 수 있지만, 응력의 집중 현상은 완화되어 응력집중으로 인한 섬유파손의 가능성은 더 줄어들게 된다. 즉, 충격 에너지가 분산되어 후프층의 섬유손상을 억제하였음을 시사한다. 후프층이 연속으로 적층된 BM은 헬리컬층과의 접합 계면이 단일 구역에 형성됨에 따라, 10 J 대비 섬유 파손 범위가 더 크게 진전되었다.
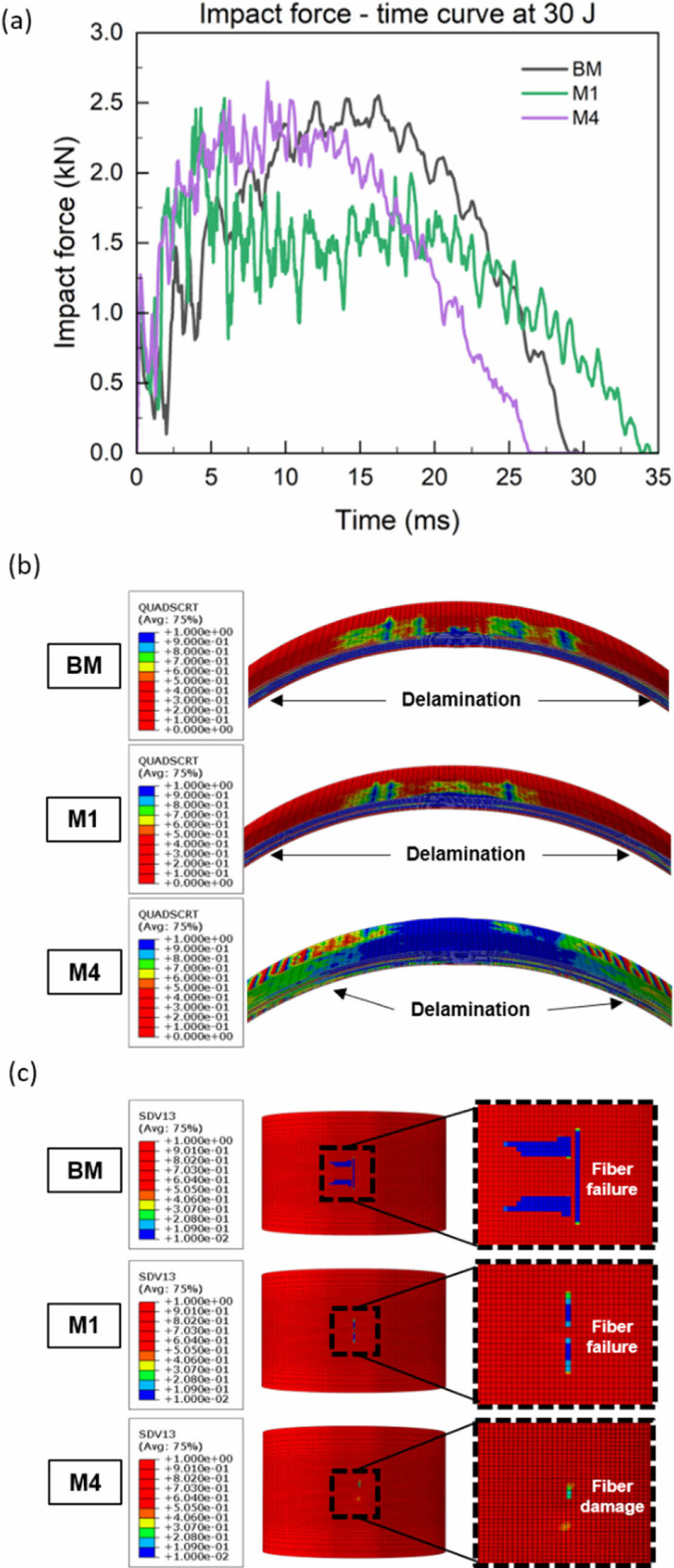
Fig. 8a는 충격 에너지 30 J에서 각 모델에 나타난 충격거동을 보여준다. 10 J 및 20 J에서 M1과 M4의 경우 BM에 비해 최대 충격력이 더 크게 나타났으나, 30 J의 경우 내부 손상에 의해 BM과 비슷한 수준으로 나타났다. Fig. 8b는 각 모델의 층간분리 손상영역을 보여준다. 세 모델 모두 층간분리가 크게 진전되었으며, 특히 후프층과 헬리컬층이 교차 적층된 M1, M4의 경우 층간분리가 더 넓은 범위에서 발생하였다. Fig. 8c는 각 모델의 후프층에서 발생한 섬유파손 영역을 보여준다. BM의 경우 CFRP 후프층의 섬유파손 영역이 20 J에 비해 진전되었으며, M4의 경우 CFRP 후프층에 섬유손상이 발생하였다. 그러나 M1의 경우 섬유파손 영역이 20 J 대비 진전되지 않은 것으로 나타났다. 이러한 결과는 20 J에서 분석한 것처럼 후프층과 헬리컬층의 교차 적층에 의해 층간분리가 크게 나타나면서 충격 에너지가 분산된 결과로 분석된다.
결론적으로 후프층과 헬리컬층을 교차하여 적층하게 되면 계면에서 층간분리가 크게 일어나게 되고 층간분리에 의해 충격 에너지가 분산되어 후프층에 발생하는 섬유파손을 억제하였다. 특히, 후프층이 상대적으로 더 분산되어있는 M4의 경우 BM과 M1에 비해 섬유손상이 더 적게 발생하였으며, 이는 복합재료 압력용기 설계 시 적층 순서가 충격 에너지 분산 및 발생하는 충격 손상 모드에 중요한 영향을 미치는 요소임을 보여준다.
4.3 파열압력 해석에 따른 용기 내압성능 평가
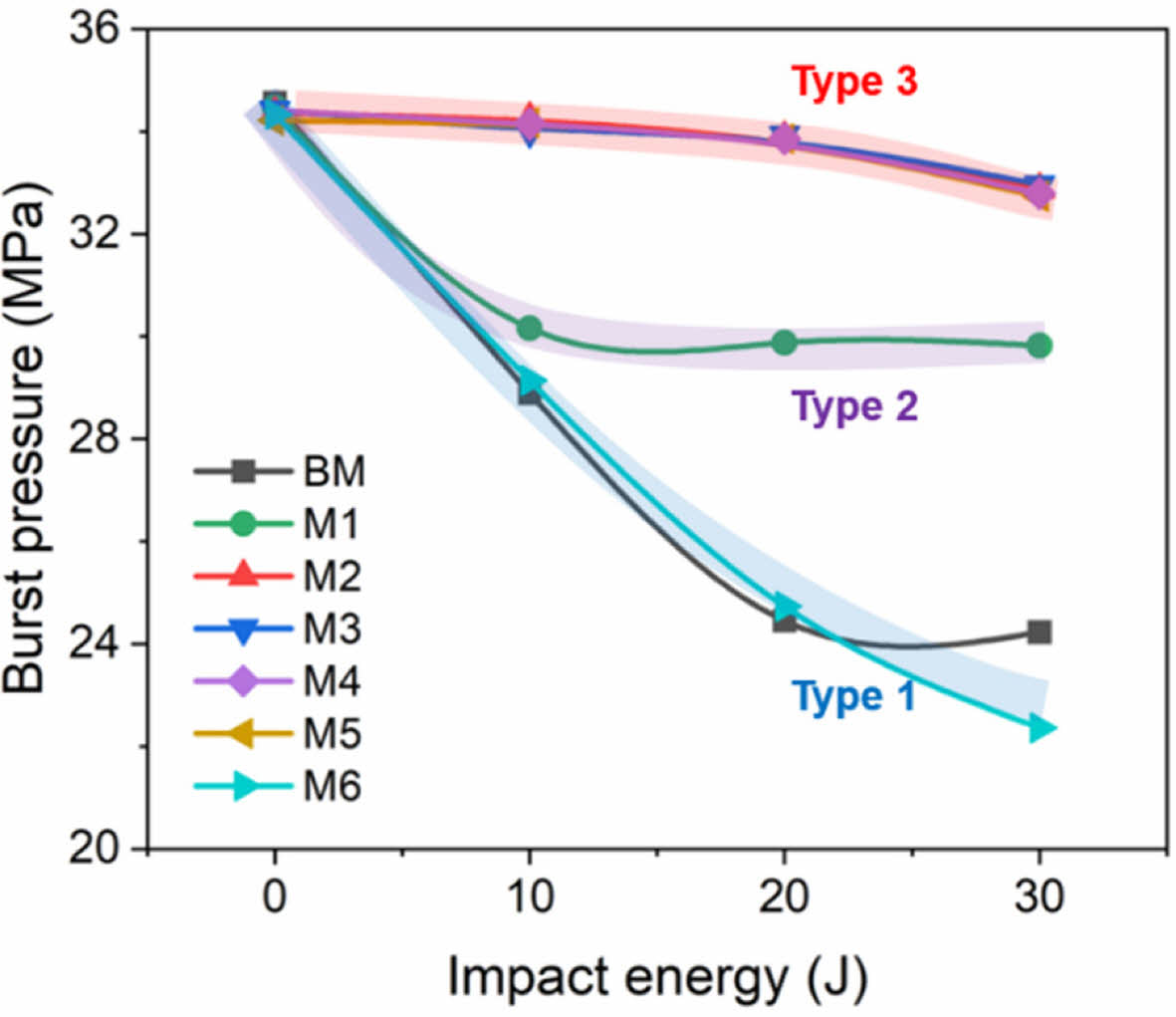
Fig. 8은 7가지 모델에 대해 충격 에너지 변화에 따른 잔류 파열압력 해석 결과를 보여준다. 잔류 파열압력 결과의 경향성에 따라 세 가지 유형 (Type)으로 분류하였다. Type 1의 경우 10 J에서 30 J로 증가함에 따라 잔류 파열압력이 지속적으로 감소하는 경향을 보이는 유형으로 BM과 M6이 이에 해당한다. 충격 에너지가 증가함에 따라 후프층의 섬유파손 영역이 진전 및 확대되어 잔류 파열압력이 저하된 것으로 분석된다. Type 2는 10 J의 충격 에너지에서 잔류 파열압력이 감소하였으나 이후 충격 에너지 증가에도 일정하게 유지되는 경향을 보였으며, M1이 이에 해당한다. 충격 에너지 10 J에서는 후프층에 섬유손상이 발생하였으나 이후 충격 에너지가 증가하여도 섬유손상이 진전되지 않아서 나타난 결과로 해석되었다. Type 3는 M2~M5가 이에 해당한다. 10 J과 20 J에서는 후프층에 섬유손상이 발생하지 않아서 파열압력이 비슷한 수준으로 유지되었지만, 30 J에서 섬유손상에 의해 소폭 감소하는 경향을 나타냈다.
BM은 30 J 충격 후 잔류 파열압력이 24.2 MPa로 초기값 34.6 MPa에 비해 30.1% 감소하였다. 후프층과 헬리컬층을 교차 적층한 M1 모델은 동일 조건에서 30.2 MPa를 보여 12.5% 감소하였으며, M4 모델은 33.2 MPa를 유지해 감소폭이 3.5%로 가장 작았다. 이는 M4에서 관찰된 후프층 섬유손상 면적이 BM 및 M1과 비교하였을 때 더 작게 나타났기 때문이다. 결과적으로 후프층과 헬리컬층을 교차 적층한 모델이 충격으로 인한 파열압력 감소가 더 적게 나타나는 것을 알 수 있다.
이러한 결과는 용기의 파열압력 및 내압 성능이 후프층의 섬유파손 발생 여부에 지대하게 영향을 받으며, 후프층과 헬리컬층의 교차 적층이 후프층의 섬유파손을 억제하는데 도움이 될 수 있음을 의미한다. Fig. 9 

본 연구에서는 복합재료 압력용기의 적층 순서 변화가 용기에 발생하는 충격 손상 및 잔류 파열압력에 미치는 영향을 분석하였다. 유한요소해석 모델을 기반으로 층내 손상과 층간 박리의 진행을 평가하였으며, 이를 통해 용기에 대한 적층 순서가 용기의 내압성능에 미치는 중요성을 확인하였다. 유한요소해석 결과를 통해 후프층의 배치가 충격 하중을 분산하는 데 중요한 영향을 미치며, 특히 후프층과 헬리컬층이 교차하여 적층되면 내부적으로 층간분리 손상은 더 크게 발생하나 이로 인해 섬유 손상이 감소하여 파열압력의 저하는 억제되는 것으로 나타났다.
이러한 결과는 복합재 압력용기의 충격 안전성을 향상시키는데 있어 최적의 적층 순서를 설계하는 것이 중요함을 시사한다. 향후 연구에서는 실험적 검증을 통해 본 연구에서 제안한 해석 모델의 신뢰성을 추가로 평가하고, 다양한 충격 하중 조건에서 충격 손상 및 내압 성능에 미치는 영향을 분석하고자 한다.

본 연구는 한국과학기술연구원(KIST)의 기관고유 연구과제(2Z07041)와 산업통상자원부의 소재부품기술개발사업(RS-2024-00433057, NO.20021913)이 지원하는 연구 과제로 수행되었습니다. 지원에 대해 진심으로 감사드립니다.