In this study, mechanical properties of woven composites were analyzed and predicted under tensile loading conditions using a deep learning approach based on their weaving structures. Composites materials with different weaving patterns were modeled as 4×4 meso scale representative volume elements (RVE), and finite element analysis (FEA) was conducted under tensile load conditions. Elastic modulus values resulting from FEA were compiled into a database reflecting various weave geometries, which served as training data for machine learning models. To train these models in capturing the relationship between weaving patterns and corresponding elastic moduli, geometric pattern information was encoded into binary matrix variables consisting of 1 and 0 and used as input data.

본 연구에서는 직물 복합재의 직조 구조를 바탕으로, 인장 하중 조건에서 기계적 물성이 딥러닝 모델을 통해 분석 및 예측이 진행되었다. 서로 다른 직조 패턴을 가진 직물 복합재가 4×4 규모의 meso scale Representative Volume Elements (RVE)로 모델링 되었고, 인장 하중 조건에서 유한 요소 해석이 수행되었다. 유한 요소 해석 결과를 기반으로 직조 형상에 따른 탄성 계수 값이 데이터베이스로 구축되었으며, 이를 학습데이터로써 딥러닝 모델이 학습되었다. 직조 패턴에 따른 탄성 계수 관계를 딥러닝 모델에 학습시키기 위해, 직조 패턴의 기하학적 형상 정보를 1과 0으로 구성된 행렬 형태의 변수로 변환하였고 입력 데이터로 사용되었다.

Keywords: 섬유 강화 복합재료(Fiber reinforcement composite), 직물 복합재(Woven composite), 딥러닝(Deep learning), 유한 요소 해석(Finite element analysis), 심층신경망(Deep neural network)

섬유 강화 복합재료(Fiber reinforcement composites, FRP)는 높은 비강도와 비강성을 가지며, 우수한 성형성으로 인해 스포츠 장비, 자동차, 로봇 및 항공우주 산업 등 다양한 분야에서 사용되고 있다[1-3]. 그 중 직물 FRP는 서로 직조된 복합재 원사에 수지가 함침되어 있는 복합재료 구조로써, 한 방향으로만 우수한 기계적 특성을 보이는 단방향 FRP에 비해 직물 FRP는 종 횡 방향 모두 상대적으로 높은 기계적 특성을 보이는 것으로 알려져 있다[4]. 현재까지 고전 적층판 이론(Classical Lamination Plate Theory, CLPT), 또는 대표 체적 요소(Representative Volume Element, RVE)를 이용한 직물 FRP의 기계적 거동 및 손상 특성을 분석하고 예측하는 연구가 활발히 진행되었다[6-9]. 그러나, 복합재 원사가 얽혀 있는 패턴, 원사의 두께, 폭과 같은 기하학적 요소 및 직조되는 과정에서 생긴 굴곡 각도 등 다양한 요인들로 인해 기계적 특성 값이 달라지며, 이에 따라 물성이나 거동을 예측하기에 어려움이 따른다[5]. Hwang 등[6]은 복합재 원사의 경로를 함수로 정의하고 이를 고전 적층판 이론과 결합하여 평직 타입 직물 복합재의 탄성계수, 전단계수 및 푸아송 비를 예측하였다. Li 등[7]은 사영 요소 방법(Projective Element Method, PEM)을 이용하여 높은 정확도를 갖는 평직 및 능직 CFRP의 RVE 모델을 설계하였고 압축 실험 및 해석을 통해 검증하였다. 또한 Jin 등[8]은 meso scale RVE 모델을 생성하고 인장, 압축 전단 하중에서의 유한 요소 해석을 통해 ABD 강성 행렬을 예측하였고, Choi 등[9]은 직조 구조의 굴곡 각도를 반영하여 점진적 파괴 모델을 적용해 모델링 기법의 적합성을 검증하였다. 이와 같은 기존 연구들은 직물 복합재의 해석 정확도를 높일 수 있는 것으로 나타내었지만, 모델링 과정의 복잡성과 긴 계산 시간, 높은 비용 등의 한계를 가지고 있다[10,11]. 따라서 이러한 한계로 인해 최근에는 머신 러닝 및 딥 러닝 모델을 활용한 연구가 시도되고 있으나, 대부분의 연구가 평직(Plain), 능직(Twill), 사틴(Satin)과 같은 기본적인 직조 패턴에 국한되어 있고, 다양한 비균일 패턴에 대한 연구가 필요한 실정이나, 여전히 많은 시간과 비용이 소모되는 실험과 해석적 검증이 요구되고 있는 실정이다[6-11]. 이러한 문제를 해결하고자, 본 연구에서는 기본 직조 패턴뿐 만 아니라 비균일한 패턴을 가진 직물 복합재의 기계적 물성을 효과적으로 예측하고 설계할 수 있는 딥 러닝 모델이 제안되었다. 이를 위해 3,000개의 비균일한 패턴이 적용된 4×4 meso scale RVE model이 구축되어 인장 유한 요소 해석이 수행되었고, 그 결과를 바탕으로 직조 패턴에 따른 탄성계수가 데이터베이스로 구축되었다. 또한, 데이터베이스 구축 과정에서 딥 러닝 모델의 효율적인 학습을 위해 데이터 전처리 작업이 병행되었으며, 직조 패턴의 경사(Warp)와 위사(Weft)가 얽혀있는 구조가 1과 0으로 구성된 4×4 행렬로 표현되었다. 최종적으로, 구축된 데이터베이스를 기반으로 딥 러닝 모델이 학습되었으며, 직조 패턴에 따른 탄성계수가 예측되었다.

2.1 직물 CFRP의 meso scale RVE 모델
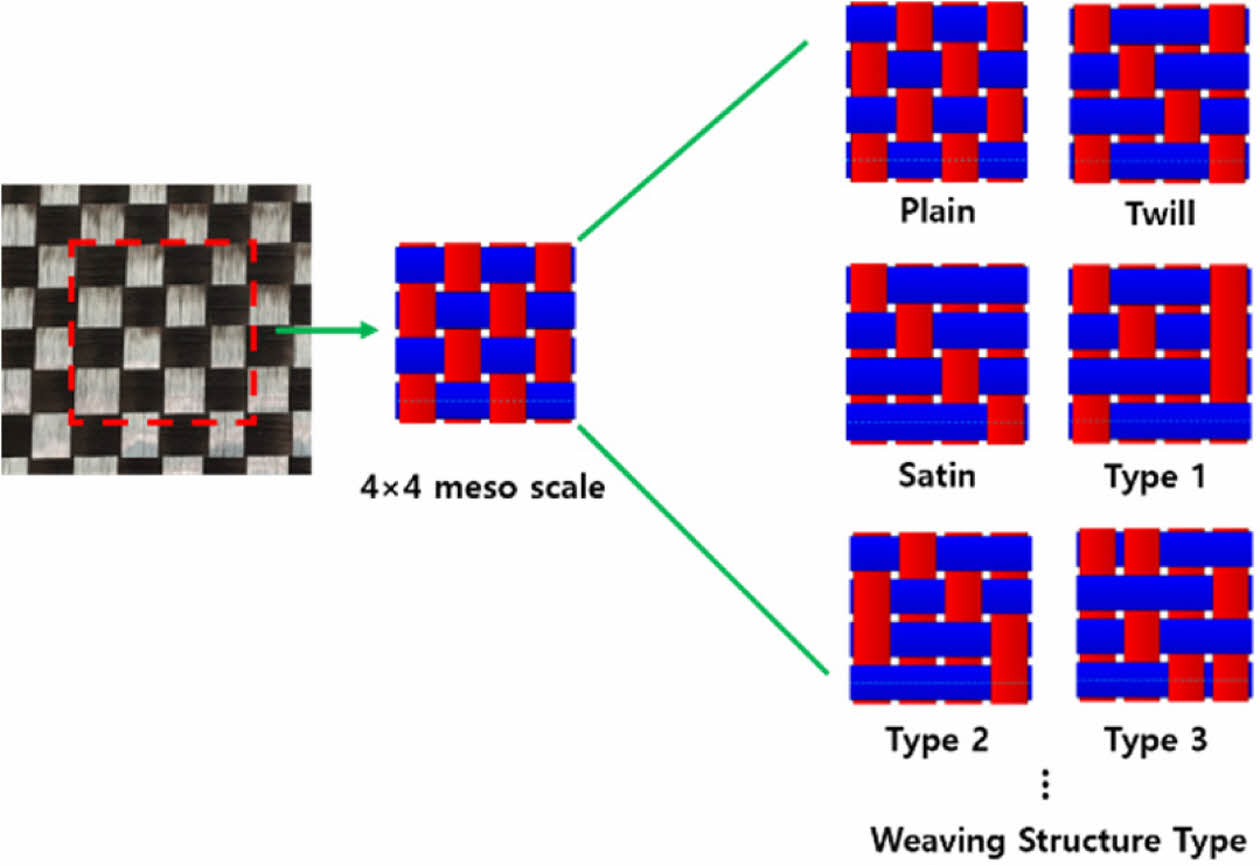
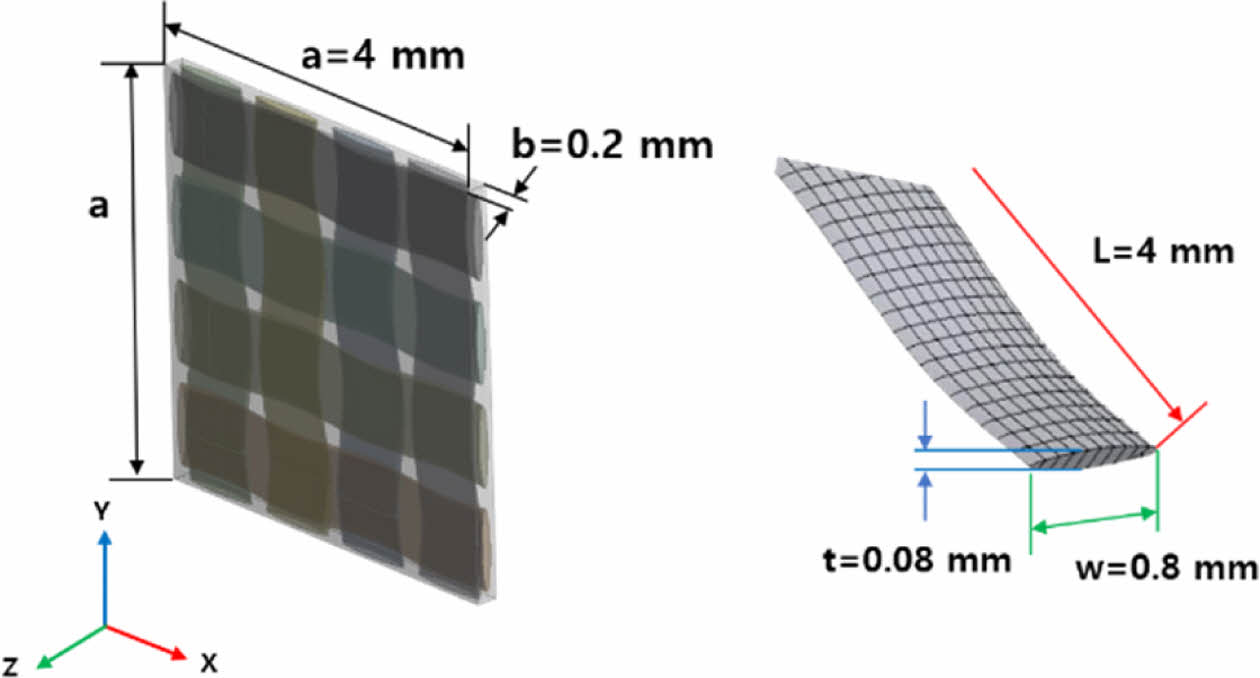
본 연구에서는 직물 CFRP에서 직조 패턴에 따른 탄성 계수 차이를 분석하기 위해 Fig. 1과 같이 평직, 능직, 사틴의 기본 구조뿐만 아니라 다양한 비균일 패턴까지 포함되는 4×4 meso scale RVE 모델이 생성되었다. 생성된 직물 CFRP 모델은 복합재 원사와 수지로 구성된다. 그리고 직물 FRP의 기하학적 요소는 Fig. 2와 같이 원사의 경우 폭(w), 두께(t), 길이(L)로, 수지의 경우 가로, 세로 길이(a)와 두께(b)로 정의된다. 이러한 기하학적 형상은 오픈 소스 프로그램인 TexGen을 통해 생성되었다[12].
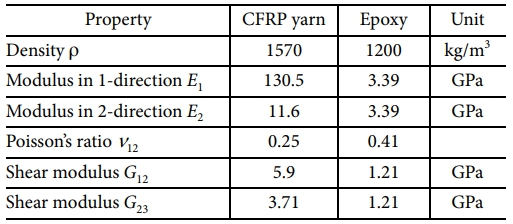
또한 직물 CFRP는 T700 탄소 섬유와 에폭시로 제작되었고, 섬유의 부피분율은 0.5로 설계되었다. 평직 CFRP의 복합재 원사와 에폭시 수지의 물성은 Table 1에 제시되어 있으며, Cao 등[13]이 수행한 인장실험을 통해 검증되었다.
2.2 유한 요소 해석
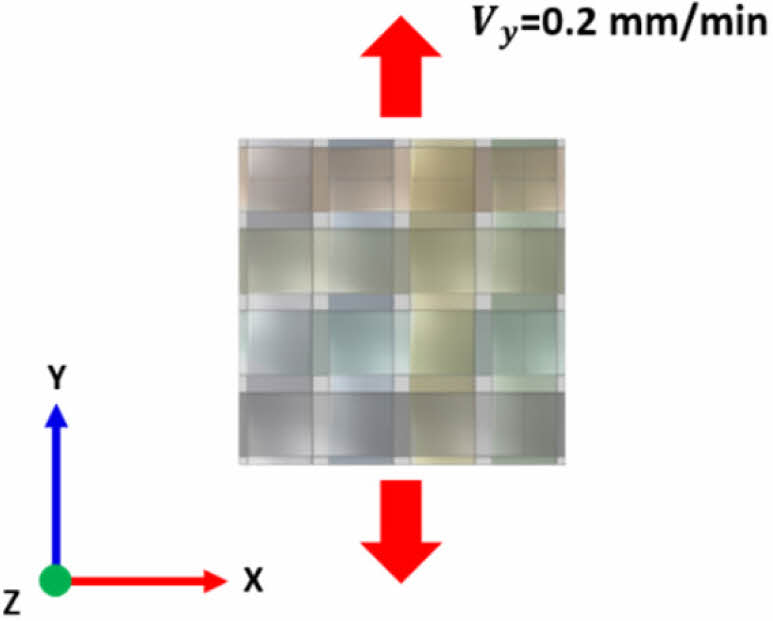
생성된 3,000개의 상이한 직조 패턴을 갖는 4×4 meso scale RVE 모델에 대하여 Ansys를 통해 인장 해석이 수행되었으며, 인장 해석 시 적용된 경계 조건은 Fig. 3에 나타나 있다. 이러한 인장 해석은 전체 재료의 특성을 대표하는 최소 단위 부피 요소인 RVE 모델을 통해 수행되었다[14,15]. 직물 CFRP의 meso scale RVE 모델은 직조 패턴뿐 만 아니라 복합재 원사의 각도 및 경로, 수지 영역과 같은 구조적 특성이 포함되어 있다[8]. 또한 직물 CFRP RVE 모델에서 섬유와 수지의 특성을 균질화하기 위해 주기적 경계 조건(Periodic Boundary Condition, PBC)가 적용되었다. PBC는 RVE 모델 경계에서 변위와 응력이 연속적으로 유지되도록 설정하여, RVE가 전체 재료의 반복적이고 균질한 특성을 나타내도록 하는 경계 조건이다[15]. 직물 CFRP의 RVE 모델에 적용된 주기적 경계 조건은 Xia 등[15]이 제안한 식 (1)과 (2)와 같이 적용되었다.



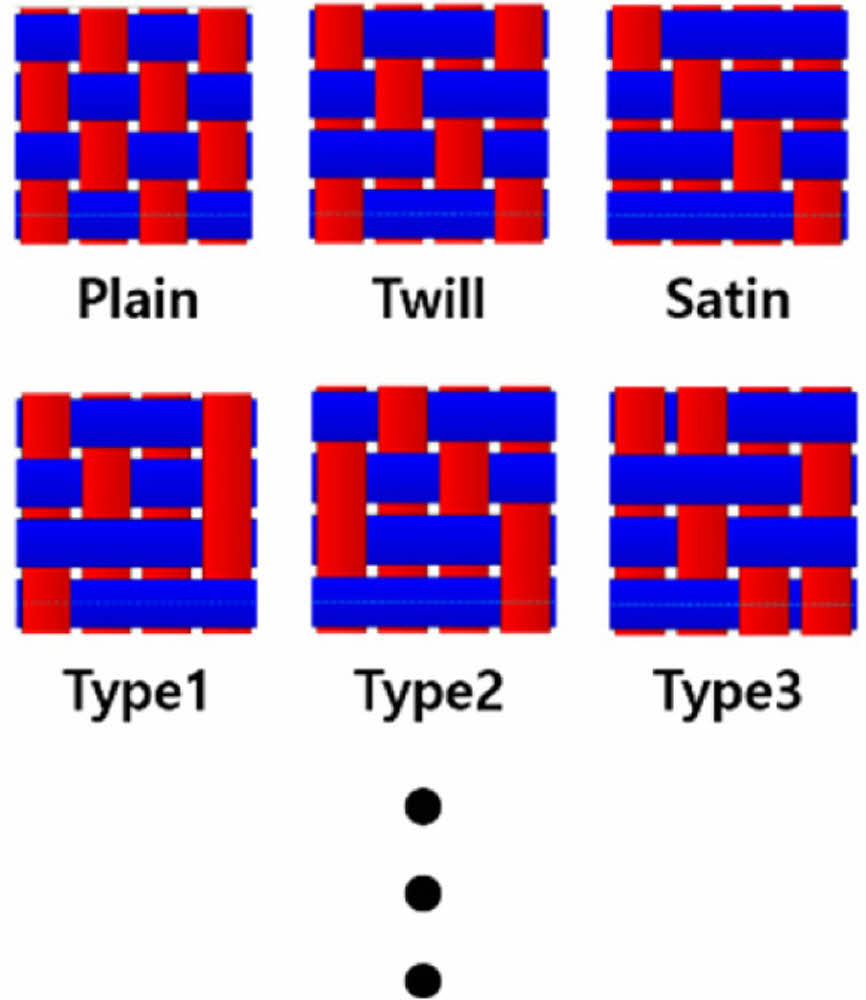
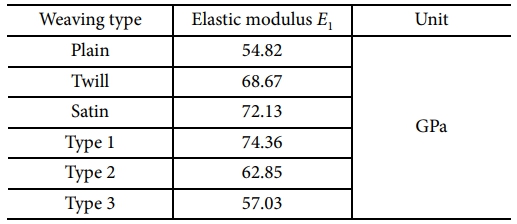
위 식 (1)에서 e_ik는 평균 변형률을, u_i^*는 경계 표면에서의 주기적 변위 성분을 나타낸다. 또한, 식 (2)의 x_k^j+와 x_k^j-는 주기적 경계 조건이 적용된 YZ 평면에서 X방향을 따라 위치한 RVE 모델의 반대면 좌표를 의미한다. 이때 인장 속도 V_j는 0.2 mm/min으로 설정되었으며, 초기 길이의 5%에 해당하는 2 mm의 변위가 부여되었다. 위와 같은 조건하에서 3,000개의 직조 패턴을 갖는 RVE 모델의 인장 해석이 수행되었고, 직조 패턴 별 탄성 계수 결과로 데이터베이스가 구축되었다. 평직 직물 CFRP에 대한 인장 실험은 Cao 등[13]에 의해 수행되었으며, 위 실험에서 탄성계수는 54.32 GPa가 도출되었고, 본 연구의 FEA에서는 54.82 GPa의 탄성계수가 도출되었다. 위 두 결과의 일치도는 98.1%로 나타나, 본 해석이 높은 정확성을 갖고 있음이 확인되었다. 그리고 Fig. 4에서는 평직, 능직, 사틴과 함께 3가지의 비균일 패턴이 포함된 대표적인 RVE 모델이 나타나 있으며, Table 2는 FEA를 통해 계산된 대표적인 직물 CFRP 모델의 탄성 계수를 보여주고 있다.

3.1 데이터 전처리
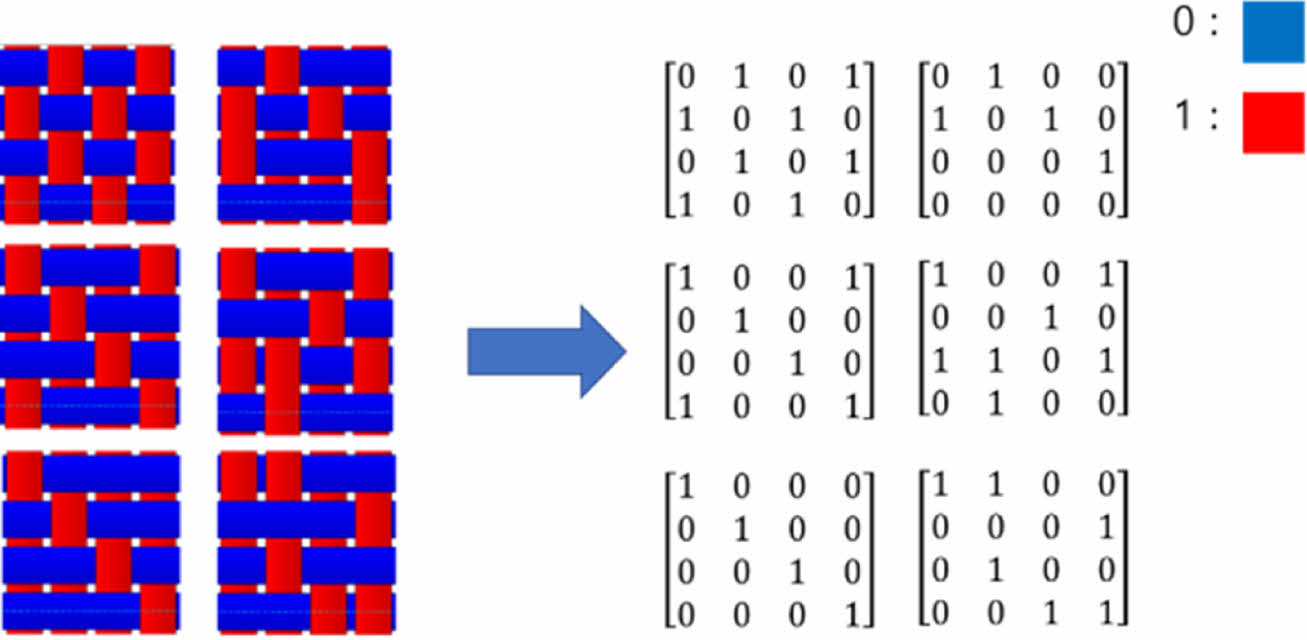
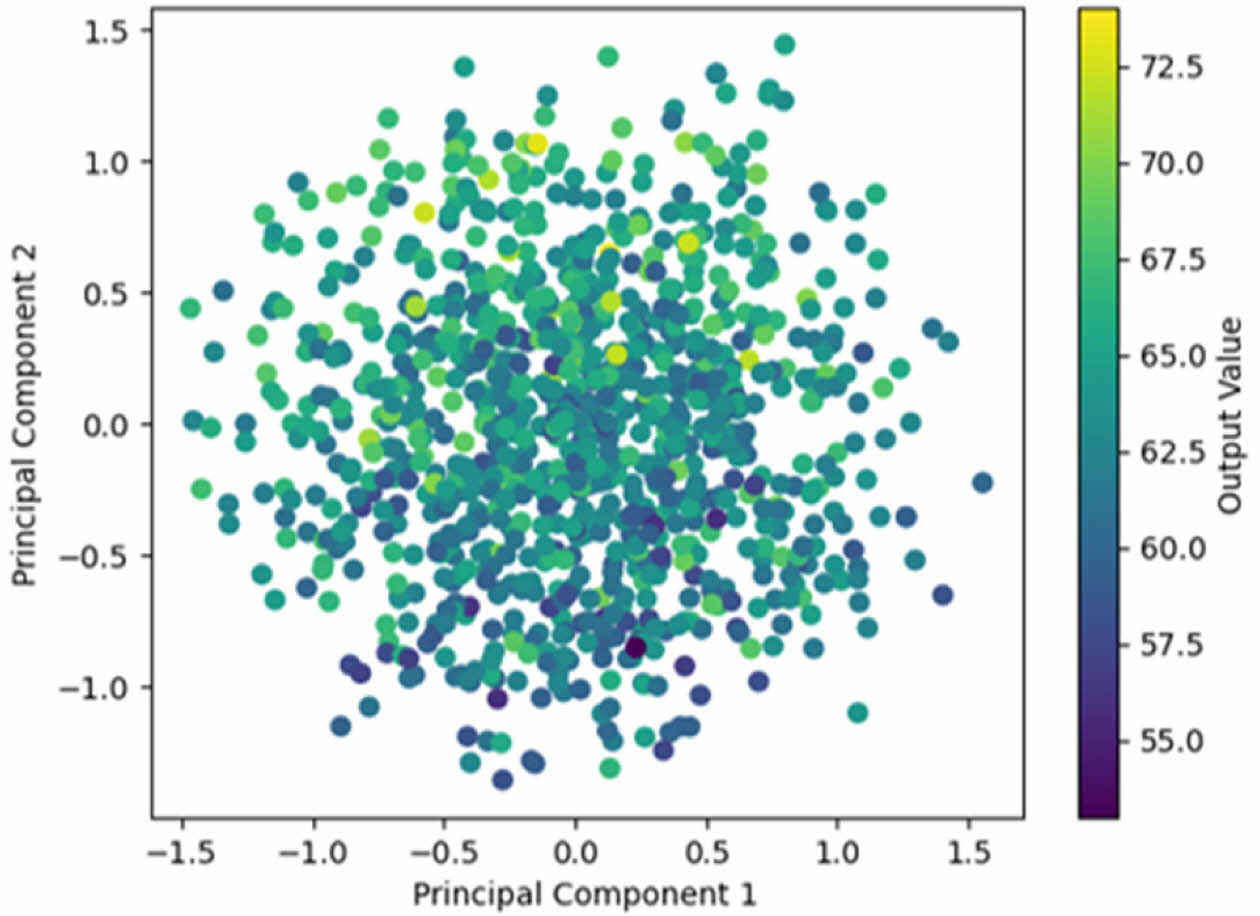
직조 패턴에 따른 탄성계수 차이가 심층 신경망 모델에 높은 정확도로 학습될 수 있도록 데이터 전처리가 수행되었다. 데이터 전처리는 데이터 내에 존재하는 노이즈를 제거하고 의미 있는 특징을 추출함으로써 신경망 모델의 학습 안정성을 높이는 과정이다[16]. 특히 직조 구조의 특징을 효과적으로 표현하기 위하여, 전처리 과정에서 Fig. 5와 같이 warp가 위에 위치하면 1, weft가 위에 위치하면 0으로 정의하여 직조 구조를 16개의 1과 0으로 구성된 4×4 행렬 형태로 나타내었다. 또한 신경망 모델의 과적합 방지 및 예측 정확도 향상을 위해 주성분 분석(Principal Component Analysis, PCA) 기법이 적용되어 데이터의 차원이 17 차원에서 2 차원으로 축소되었다. 여기서 PCA란 데이터의 분산이 가장 큰 방향을 첫 번째 축으로 설정하고, 이어서 다음으로 분산이 크면서 이전 축들과 직교하는 축들을 추가하여 데이터를 고차원에서 저차원으로 투영시키는 방법이다[16]. 그 결과 기존 4×4 행렬과 이에 따른 탄성계수로 구성된 17 차원 입 출력 데이터는 2차원으로 축소되었으며, 차원이 축소된 데이터의 분포는 Fig. 6과 같이 나타난다.
3.2 심층 신경망 모델
직물 CFRP의 직조 패턴에 따른 탄성계수를 예측하기 위해 심층 신경망 모델(Deep Neural Network, DNN)이 사용되었다. 전체 3,000 개의 데이터 세트는 9:1의 비율로 나뉘어, 그 중 2,700 개는 모델 학습을 위한 데이터로, 나머지 300 개는 학습된 모델의 성능 평가를 위한 데이터로 활용되었다. 사용된 심층 신경망 모델은 입력층, 은닉층 및 출력층으로 구성되어 있으며, 모델 학습을 위해 입력층에 2,700 개의 학습 데이터가 입력되었다. 이후 은닉층에서는 입력 데이터와 출력 데이터 사이의 관계가 학습되었으며, 최종적으로 출력층에서 직조 패턴에 따른 탄성계수 값이 예측되었다. 이때 높은 예측 정확도를 달성하기 위해 심층 신경망 모델의 하이퍼 파라미터가 최적화되었다. 최적화 과정에서 모델이 한 번에 학습하는 데이터 수인 배치 크기(Batch size)는 32 개로 설정되었으며, 학습 반복 횟수인 에포크는 100 회로 설정되었다. 또한 활성화 함수로는 기울기 소실 문제를 완화하고 학습 효율성을 높이는 ReLU가 사용되었고, 최적화 함수로는 학습률을 효율적으로 조정할 수 있는 Adam이 적용되었다[15]. 그리고 모델의 학습 성과를 평가하기 위해 평균 절대 오차(Mean Absolute Error, MAE) 손실 함수가 사용되었으며, 이는 학습 반복 과정에서 식 (3)과 같이 계산되었다.



위 식 (3)에서 y는 FEA를 통해 계산된 탄성계수 값이, ŷ는 심층 신경망 모델이 예측한 탄성계수 값이다. 그리고 n은 데이터의 총 개수를 의미한다.

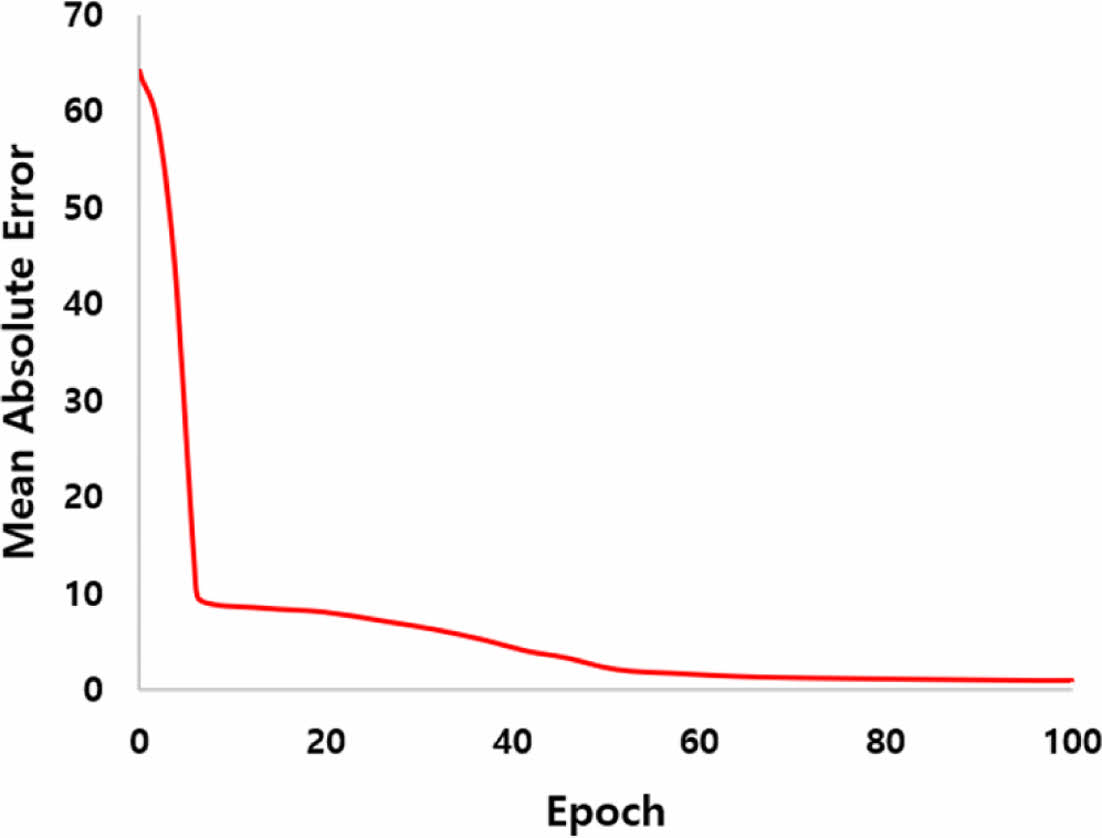
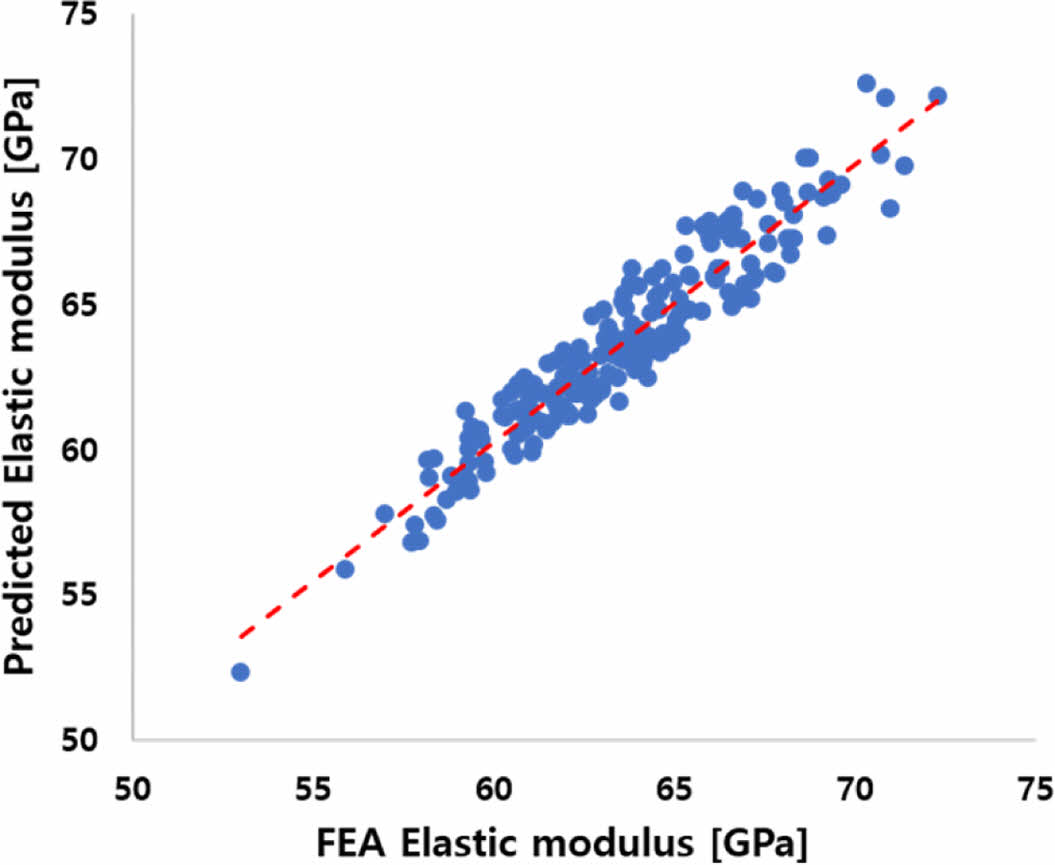
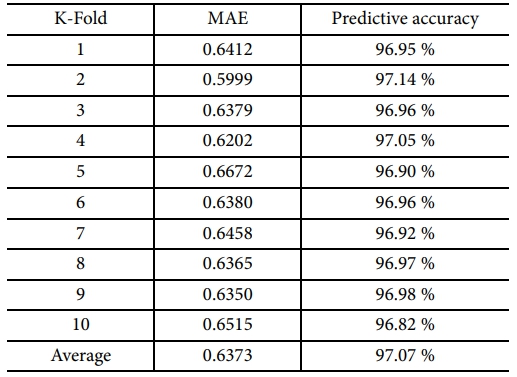
직물 CFRP의 직조 패턴에 따른 탄성계수가 학습된 심층 신경망 모델의 성능은 테스트 데이터를 통해 평가되었다. 또한, 모델의 예측 정확도를 평가하기 위해 K겹 교차 검증(K-fold cross validation)이 적용되었으며, 이는 데이터 세트를 K개의 동일한 크기로 분할한 후, 각 분할을 한 번씩 테스트 데이터로 사용하고 나머지 분할을 학습 데이터로 사용하는 과정을 K번 반복하여 모델의 성능을 평가하는 방법이다[17]. 이를 통해 데이터의 활용도가 극대화되고, 모델의 성능이 보다 정확히 평가될 수 있다. 3,000 개의 직조 패턴 데이터가 300 개씩 10 개의 그룹으로 나누어졌으며, 각 그룹이 한 번씩 테스트 데이터로 사용되어 총 10 회의 학습 및 평가가 이루어졌다. 각 그룹에 대한 독립적인 평가를 통해 데이터 분할 방식에 따른 결과의 변동이 최소화되었고, 모델의 안정성이 확인되었다. 이 과정에서 평균 절대 오차가 지표로 사용되어 모델의 성능이 평가되었으며, 각 반복 학습에서 100 번의 에포크 동안 오차가 산출되었다. Fig. 7은 대표 그룹의 MAE가 100 번의 에포크에 걸쳐 점진적으로 감소하며 안정적으로 수렴하는 경향을 나타내고 있으며, 이를 통해 모델의 예측 정확도가 정량적으로 분석되었다. 10 개의 그룹에 대한 반복 학습 결과는 Table 3에 제시되어 있으며, 최고 예측 정확도는 97.14%, 최저 예측 정확도는 96.82%, 그리고 평균 예측 정확도는 97.07%로 나타났다. 그리고 Fig. 8에서는 Fold 5에서 FEA로 산출된 탄성 계수와 심층 신경망 모델이 예측한 탄성 계수가 비교된 결과를 나타내며, 직물의 축 대칭성으로 인해 입력 데이터는 달라도 동일한 탄성 계수를 출력하는 경우가 존재하여 각 학습마다 예측 정확도에 차이가 발생한 것으로 판단된다.
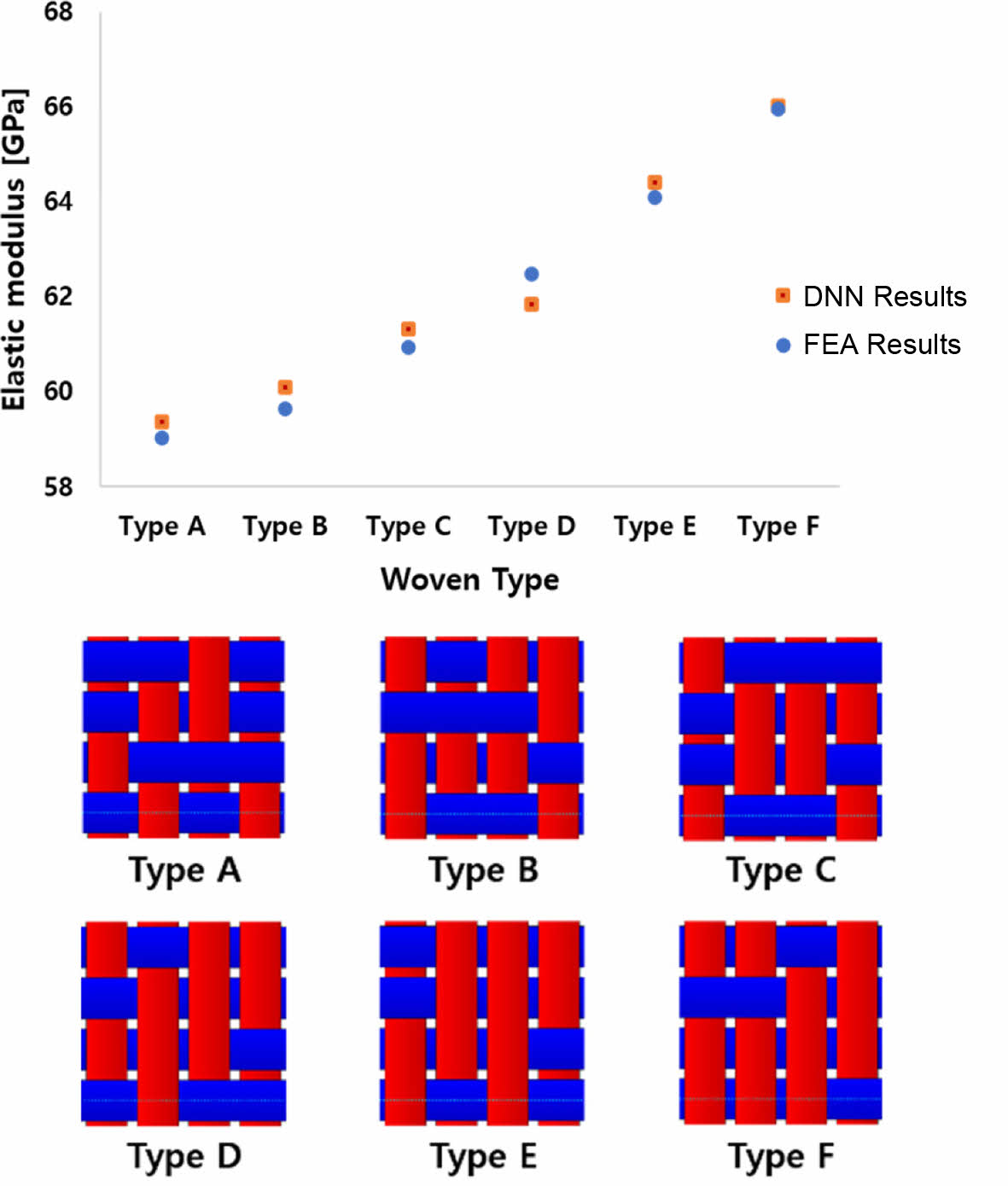
또한 모델 학습 및 성능 평가에 사용되지 않은 3,000개의 직조 패턴 외에 추가 데이터를 활용하여 DNN의 예측 정확도를 검증하였다. Fig. 9는 Fold 5에 대한 검증 결과를 나타내며, Type A부터 F까지의 직조 패턴을 갖는 6개의 데이터를 대상으로 진행되었다. 이 중 가장 높은 예측 정확도는 Type F에서 98.6%을 기록하였으며, 가장 낮은 정확도는 Type D로 94.5%로 나타났다. 이때 Fold 5는 평직 패턴 데이터가 성능 평가에 사용된 경우이며, Table 4에는 해당 직조 패턴의 탄성계수에 대해 실험, FEA 그리고 DNN 예측 결과 간의 비교가 나타나 있다.

본 연구에서는 심층 신경망 모델을 통해 직물 복합재의 직조 패턴에 따른 탄성계수의 예측 가능성이 확인되었다. 이를 위해 3,000 개의 다양한 직조 패턴이 포함된 4×4 meso scale RVE 모델이 구축되었고, 유한 요소 해석을 통해 각각의 탄성계수가 계산되었다. 직조 구조는 warp과 weft의 교차 형태가 1과 0으로 나타낸 4×4 행렬로 표현되었으며, PCA를 통해 데이터 차원을 축소한 후 심층 신경망 모델에 학습되었다. 이를 통해 직물 CFRP의 복잡한 직조 패턴이 탄성계수에 미치는 영향이 빠른 시간 내 높은 정확도로 예측될 수 있음이 확인되었다. 이러한 연구는 직물 복합재의 직조 패턴에 따른 기계적 특성을 효과적으로 예측하고 설계의 효율성을 높일 것이라 사료된다. 특히, 직조 구조를 1과 0으로 표현하는 데이터 전처리 과정과 차원 축소를 통한 심층 신경망 모델의 성능 최적화는 설계 시간을 단축할 뿐만 아니라, 복합재의 구조 설계 과정에서의 비용 절감에도 기여할 수 있을 것으로 평가되고 있다. 향후 연구에서는 복합재 원사의 얽힌 구조에서 발생하는 굴곡 각도 변화, 원사 간의 상호작용 등 다양한 기하학적 요소들이 기계적 물성에 미치는 영향 분석을 통해, 정확도와 신뢰도를 한 단계 더 높일 수 있는 예측 모델 개발이 필요할 것으로 기대된다.

이 연구는 2025년도 산업통상자원부 및 한국산업기술기획평가원(KEIT) 연구비 지원에 의한 연구임 (‘20017947’).