- Prediction of Residual Stress in Composites by Cooling Rates Using a Viscoelastic Model
Jung-Hyeon Rhim*, Wie-Dae Kim*†
* Department of Aerospace Engineering, Pusan National University
- 점탄성 모델을 이용한 냉각 속도에 따른 복합재의 잔류응력 예측
임정현* · 김위대*†
This article is an open access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
In thermoset composite manufacturing using the autoclave process, residual stresses are generated due to high temperature and pressure conditions, potentially causing thermal deformation and degrading the mechanical performance and dimensional stability of the final product. The cooling stage is particularly critical, as it induces the highest residual stresses, directly affecting the quality and stability of the composite. This study aims to predict residual stress distribution under varying cooling rates by implementing a coupled temperature–displacement analysis using the commercial finite element software ABAQUS and USER SUBROUTINE. A thermo-viscoelastic model was developed considering resin viscoelasticity and heat of reaction. Model reliability was validated through comparison with previous research, and residual stresses were analyzed under six cooling rate conditions.
오토클레이브를 사용하는 열경화성 복합재 성형 공정은 고온과 고압 조건에서 진행되기 때문에 성형 과정 중 다양한 요인에 의해 잔류응력이 발생하며, 이는 열변형을 유발하여 복합재 구조물의 기계적 성능과 치수 안정성을 저하시킬 수 있다. 특히, 오토클레이브 공정의 냉각 과정은 잔류응력이 가장 크게 발생하는 구간으로, 제품의 최종 품질과 안정성에 직접적인 영향을 미치기 때문에 해당 구간에서의 잔류응력 예측이 중요하다. 본 연구에서는 냉각 속도가 잔류응력 분포에 미치는 영향을 분석하기 위해 상용 유한 요소 해석 프로그램인 ABAQUS와 ABAQUS USER SUBROUTINE 기능을 활용하여 복합재 수지의 점탄성 거동과 화학 반응열을 반영한 열-구조 연계 해석 모델을 구현하였다. 구현된 해석 모델의 신뢰성은 선행 연구 결과와의 비교를 통해 검증하였으며, 이를 바탕으로 총 6가지 냉각 속도 조건에 대해 잔류응력을 예측하고 그 경향을 분석하였다.
Keywords: 열경화성 복합재(Thermoset Composite), 오토클레이브 공정(Autoclave Process), 냉각 속도(Cooling Rate), 잔류 응력(Residual Stress), 점탄성 모델(Viscoelastic Model)
열경화성 복합재는 우수한 비강도와 비강성 특성으로 인해 항공우주, 자동차, 선박, 방위 산업 등 다양한 분야에서 핵심 소재로 활용되고 있다. 특히 항공우주 산업에서는 연료 효율 향상과 이산화탄소 배출 저감을 위해 구조물의 경량화가 필수적이며, 이에 따라 복합재의 사용 비율은 지속적으로 증가하는 추세이다. 복합재는 기존 금속 대비 피로 저항성이 뛰어나고, 반복적인 이착륙에도 구조적 안정성을 유지할 수 있어 항공기 운항 효율을 향상시키는 소재로 주목받고 있다[1].
복합재 성형 공정 중 하나인 오토클레이브(Autoclave) 공정은 프리프레그(Prepreg)를 적층한 후, 진공 상태에서 고온과 고압을 가하여 성형하는 방식으로, 높은 기계적 성질과 신뢰성이 요구되는 항공우주 구조물 제작에 주로 사용된다. 하지만 이 공정은 고온과 고압 조건에서 진행되므로 성형 과정 중 다양한 요인으로 인해 잔류응력과 열변형이 발생하며, 이는 초기 설계 형상과 최종 형상 간의 오차가 발생하고 복합재 구조물의 기계적 성능 및 치수 안정성이 저하된다. 이러한 형상 오차를 보정하기 위해 제품을 재설계하고 성형을 반복하여 결과를 확인하는 과정은 상당한 시간과 비용이 요구되므로, 성형 중 발생하는 잔류응력과 열변형을 예측하기 위한 유한 요소 해석(Finite Element Analysis, FEA) 기반의 연구가 꾸준히 수행되어 왔다.
복합재 성형 시 발생하는 잔류응력과 열변형을 예측하기 위해서는 다양한 요인을 고려해야 하며, 대표적으로 복합재의 물성 변화, 몰드 형상, 적층 배열, 냉각 중 급격한 온도 변화 등이 주요 인자로 작용한다[2]. Jung은 2-D 점탄성 모델을 기반으로 온도, 경화도, 완화 시간에 따른 복합재 물성을 계산하고, 적층 배열에 따른 잔류응력과 열변형을 예측하였다[3]. Seong은 이를 확장하여 3-D 점탄성 모델을 적용하고, 평판 및 L-형상 성형 시 발생하는 잔류응력과 열변형을 예측하였다[4]. Lee는 몰드의 종류 및 표면 상태에 따라 성형 시 발생하는 잔류응력과 열변형을 예측하였으며[5], Yu는 수지(Resin)의 화학 반응열(Heat of reaction)을 고려하여 복합재 내부 온도와 경화도를 예측하였다[6].
선행 연구들[3-5]에서는 수지의 화학 반응열을 고려하지 않고, 오토클레이브 온도와 복합재 내부 온도를 동일하게 가정하여 해석을 수행하였다. 하지만 실제 성형 공정에서는 수지의 경화 과정 중 화학 반응열이 발생하므로, 복합재 내부 온도가 오토클레이브 온도와 차이를 보일 수 있다. 따라서 잔류응력을 정확하게 예측하기 위해서는 선행 연구[6]과 같이 화학 반응열을 반영한 유한 요소 해석이 필요하다. 또한, 오토클레이브 공정 중 냉각 과정은 잔류응력이 가장 크게 발생하는 구간이며, 제품의 치수 안정성에 직접적인 영향을 미치므로 냉각 과정에서의 잔류응력을 예측하는 연구가 필요하다.
이에 따라, 본 연구에서는 상용 유한 요소 해석 프로그램인 ABAQUS와 ABAQUS USER SUBROUTINE 기능을 활용하여 수지의 화학 반응열을 고려한 점탄성 모델을 구현하였다[7]. 구현된 해석 기법은 선행 연구의 결과와 비교하여 신뢰성을 검증하였으며[8,9], 이를 바탕으로 오토클레이브 냉각 과정에서 발생하는 AS4/3501-6 복합재의 잔류응력을 예측하였다. 또한, 다양한 냉각 속도 조건에 대한 추가 해석을 수행하여 냉각 속도가 잔류응력에 미치는 영향을 분석하였다.
2.1 3501-6 수지의 경화 방정식
본 연구에 사용된 3501-6 수지는 미국 Hexcel사에서 제조하였으며, 비스페놀 A(Bisphenol A)와 에피클로로히드린(Epichlorohydrin)의 반응으로 생성된 Diglycidyl Either of Bisphenol A(DGEBA) 기반의 에폭시 수지이다.
이 수지는 온도 변화에 따라 경화가 진행되며, 그 진행 정도를 나타내는 경화도(Degree of Cure, a)는 0에서 1 사이의 값으로 정의된다. 경화도가 0일 때는 수지가 액체 상태이며, 1에 도달하면 경화가 완료된 고체 상태를 의미한다.
본 연구에서는 오토클레이브 공정 중 변화하는 3501-6 수지의 경화도를 계산하기 위해, 선행 연구[10]에서 DSC(Differential Scanning Calorimetry) 실험을 통해 제시한 데이터를 바탕으로 도출된 경화 방정식을 적용하였다. 해당 경화 방정식은 식 (1)-(3)과 같다.
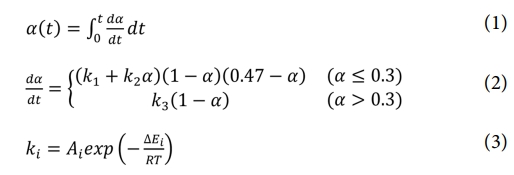
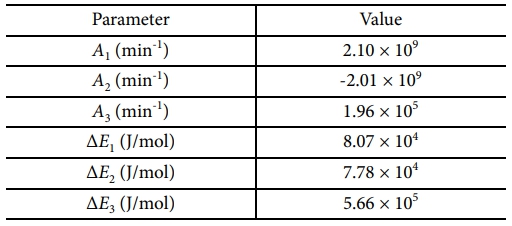
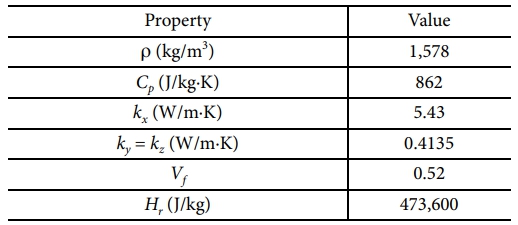
식 (3)은 Arrhenius 식으로 표현되며, ki는 반응 속도 상수, Ai는 빈도 계수(Pre-exponential factor), DEi는 활성화 에너지, R은 일반 기체 상수, T는 절대 온도를 의미한다. 3501-6 수지의 경화 방정식 상수 값은 Table 1에 정리하였다.
2.2 열전달 방정식
열경화성 복합재의 성형 과정에서는 수지의 경화 반응에 따라 화학 반응열이 발생한다. 이를 고려하여, 본 연구에서는 오토클레이브 내부에서 복합재에 전달되는 열의 거동을 푸리에(Fourier) 열전도 방정식을 사용하였으며, 식 (4)와 같이 표현된다[11].
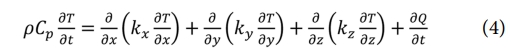
여기서, ρ, Cp는 각각 복합재의 밀도(Density)와 비열(Specific heat capacity), T는 온도, t는 시간, kx, ky , kz는 방향별 열전도도(Thermal conductivity), ∂Q/∂t은 화학 반응열 비(Heat generation rate)를 의미한다.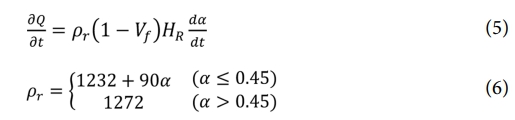
화학 반응열 비 ∂Q/∂t은 수지의 고분자 가교 반응에 의해 발생하며, 식 (5)와 같이 정의된다. 또한, 수지의 밀도 ρr은 경화도에 따라 식 (6)과 같이 정의된다. 여기서, Vf 는 섬유 체적율(Fiber volume fraction), Hr은 총 발열량(Total heat of reaction)이다. 본 연구에 적용된 상수 값은 선행 연구[8,10] 에서 제시된 실험 결과를 참조하여 Table 2에 정리하였다.
2.3 열 변형률
복합재 성형 공정에서는 오토클레이브 온도 변화에 따른 열팽창(Thermal expansion)과 수지의 경화 반응에 따른 화학 수축(Chemical shrinkage)이 발생한다. 이로 인해 열 변형률(Thermal strain)은 성형 후 형상 변형의 주요 원인이 되므로, 해석 시 반드시 고려해야 한다.
열팽창계수(Coefficient of Thermal Expansion, CTE)는 온도 변화에 따른 재료의 길이 변화를 나타내며, 화학수축계수(Coefficient of Chemical Shrinkage, CCS)는 경화 과정 중 고분자 사슬의 재배열에 의해 발생하는 부피 수축을 의미한다.
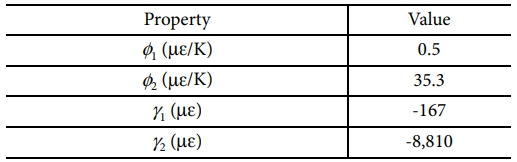
복합재는 섬유 방향(Fiber direction)과 그 수직 방향(Transverse direction)에 따라 서로 다른 열팽창 및 화학수축 특성을 가지므로, 섬유 방향에 대한 열팽창계수와 화학수축계수를 각각 f1, g1로, 수직 방향에 대한 열팽창계수와 화학수축계수는 각각 Φ2, γ2로 정의하였다. 이러한 계수들은 Micromechanical Model을 통해 계산된 값으로, 선행 연구[12]에서 제시된 결과를 사용하였으며, 해당 상수 값은 Table 3에 정리하였다.
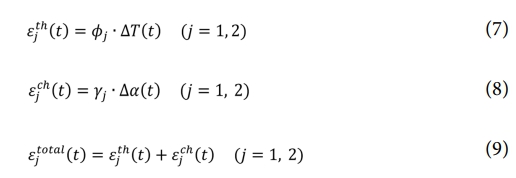
식 (7)은 온도 변화에 따른 열팽창 변형률을, 식 (8)은 경화도 변화에 따른 화학 수축 변형률을 각각 나타낸다. 이 두 식을 합산함으로써, 복합재의 총 열변형률은 식 (9)와 같이 계산된다[12].
2.4 점탄성 모델
복합재 성형 공정에서 수지는 점탄성(Viscoelastic) 거동을 보이며, 이는 경화도, 온도, 시간에 따라 변화한다. 이러한 점탄성 특성은 응력, 강성, 변형률 간의 관계로 표현되며, 식 (10)과 같이 나타낼 수 있다.
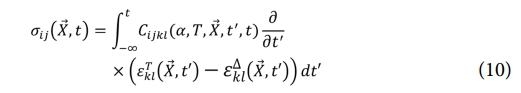
식 (10)에서 σij는 응력 텐서, εTkd는 총 변형률(Total strain), εΔkd는 비기계적 변형률(Non-mechanical strain), X̅는 위치 벡터, t,t'는 각각 현재 및 과거 시간을 의미한다. 식 (10)을 Matrix 형태로 표현하면 식 (11)과 같다.
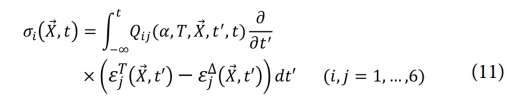
경화도가 일정하고, 초기 시간 t = 0 이전에 변형과 응력이 없다고 가정하면 식 (11)은 식 (12)로 표현된다.
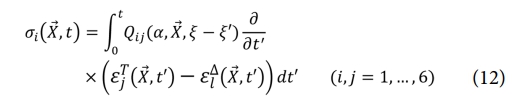
식 (12)에서 ξ,ξ'(Reduced time)는 식 (13)과 같이 정의된다. αT(Shift factor)는 경화도와 온도의 함수이며, 식 (14)와 같이 표현된다.
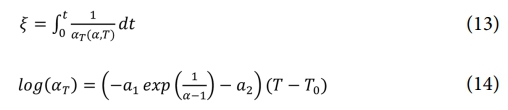
경화도에 따른 유리 전이 온도(Glass transition temperature, Tg)는 실험식을 통해 식 (15)와 같이 정의된다. Tg는 경화도에 따라 점탄성 거동과 유사한 변화를 보이므로, 이를 통해 응력 완화 시간의 경화도 의존성을 간접적으로 나타낼 수 있다. 경화도 αref = 0.98에서의 Tg를 기준으로 정의하면, 화학적 경화 함수(Chemical hardening function) f(a)는 식 (16)과 같이 표현된다. 이 함수는 응력 완화 시간의 변화에도 동일하게 적용되어 식 (17)과 같이 나타낼 수 있다.

복합재 수지의 응력 완화 거동은 선형 점탄성 모델인 일반화된 맥스웰 모델(Generalized Maxwell model)을 이용하여 식 (18)과 같이 표현된다.
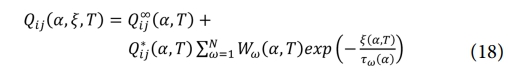
식 (18)에서 Q∝ij는 완전 완화 탄성계수(Fully relaxed modulus), Q*ij = Quij - Q∝ij 의 관계로 정의되며, Quij는 비 완화 탄성계수(Unrelaxed modulus)를 나타낸다. Ww는 가중치,ξ는 완화 시간, τw는 응력 완화 시간을 나타낸다.
온도의 영향이 일정하다고 가정하면, 식 (18)은 경화도와 시간의 함수로 단순화되어 식 (19)와 같다.
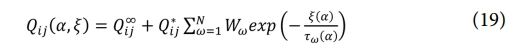
복합재의 두께가 길이와 폭에 비해 매우 작을 경우, 복합재를 횡등방성(transversely isotropic) 재료로 가정할 수 있다. 이때 유효 강성 매트릭스는 식 (20)과 같이 구성되며, 각 항들은 식 (21)-(25)와 같이 정의된다. 공통 분모인 ∧(t)는 식 (26)과 같이 나타내며, 푸아송 비(Poisson’s ratio)는 식 (27)과 같이 정의된다[12].

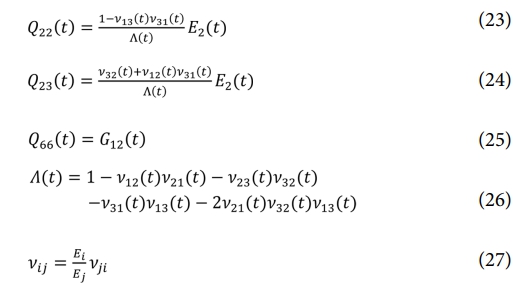
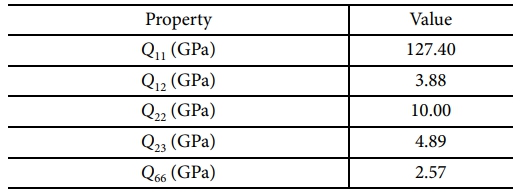
본 연구에서는 포아송 비의 비율과 섬유 방향 탄성 계수 E1을 시간에 독립적인 상수로 가정하여 복합재의 응력 완화 거동을 결정하는 주요 변수는 섬유 수직 방향의 탄성 계수 E2(t), 전단 탄성 계수 G12(t), 유효 포아송 비 V12(t),v23(t)이다. 본 연구에서 사용된 AS4/3501-6 복합재의 완화 탄성 계수는 선행 연구[12]에 제시된 실험 결과를 참조하여 Table 4에 정리하였다.
2.5 ABAQUS USER SUBROUTINE
본 연구에서는 유한 요소 해석을 위해 상용 구조 해석 프로그램인 ABAQUS를 사용하였다. 하지만, 시간 및 온도 변화에 따라 변하는 복합재 물성 변화를 반영하기 위해서는 ABAQUS의 기본 해석 기능만으로는 한계가 있으므로, ABAQUS USER SUBROUTINE을 사용하였다.
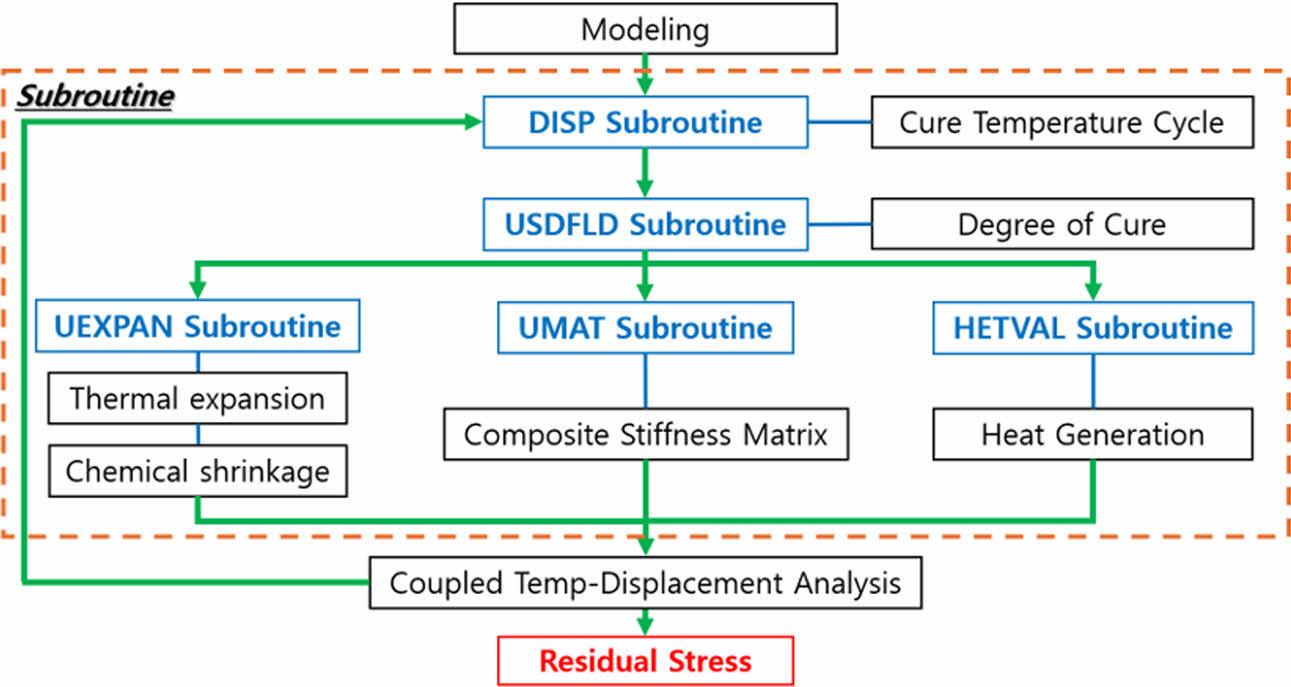
FORTRAN 언어를 기반으로 각 서브루틴을 구현하였으며, 유한 요소 해석의 전체 절차는 Fig. 1과 같은 구성에 따라 수행하였다. 이를 통해 열 및 구조 거동을 동시에 고려하는 열-구조 연계 해석(Coupled Temp-Displacement analysis)을 수행하였다.
먼저, USDFLD 서브루틴은 수지의 경화도를 계산하고, 이를 물성 변화 및 열적 특성 모델링에 필요한 입력값으로 활용하였다. UEXPAN 서브루틴은 온도와 경화도에 따른 열팽창 및 화학수축을 계산하였다. UMAT 서브루틴에서는 수지의 점탄성 거동을 반영하기 위해 일반화된 맥스웰 모델을 적용하였으며, 이를 통해 응력-변형률 관계를 구현하고 해석에 필요한 강성 행렬을 계산하였다. HETVAL 서브루틴은 경화 과정 중 발생하는 화학 반응열을 계산하여 복합재 내부의 온도 분포를 예측하는데 활용하였으며, DISP 서브루틴은 오토클레이브의 온도 및 시간을 설정하는 데 사용하였다.
이와 같은 서브루틴들은 시간 및 온도 변화에 따라 달라지는 복합재의 물성을 반영하기 위해 사용되었으며, 본 연구에서는 이를 통해 오토클레이브 성형 공정 중 발생하는 잔류응력을 예측하였다.
|
Fig. 1 Schematic of USER SUBROUTINE for ABAQUS |
|
Table 3 Thermal expansion and Chemical shrinkage Coefficients of AS4/3501-6 prepreg [12] |
3.1 유한 요소 해석 검증 모델링
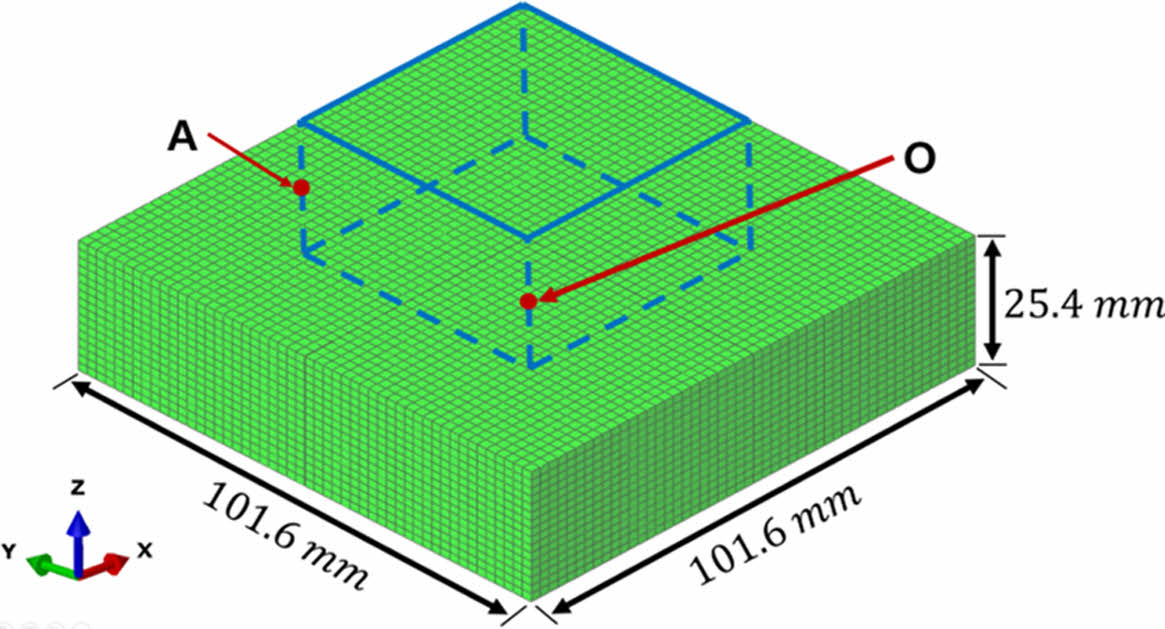
본 연구에서 구현한 유한 요소 해석 기법의 신뢰성을 검증하기 위해 선행 연구 White, Kim[9], Zhang[10]의 해석 결과와 비교하였다. White, Kim[9]은 Fig. 2와 같이 복합재 평판의 A 지점인 표면부와 O 지점인 중심부의 온도와 경화도 해석 결과를, Zhang[10]은 A 지점인 표면부의 잔류응력 해석 결과를 도출하였다. 이에 따라, 본 연구에서도 동일한 지점에서의 온도, 경화도, 잔류응력의 결과를 유한 요소 해석을 통해 도출하여 White, Kim[9]과 Zhang[10]의 결과를 비교함으로써 모델의 신뢰성을 검증하였다.
해석에 사용된 모델은 AS4/3501-6 복합재 평판이며, 적층 배열은 [0°/90°]s로 구성하였다. 해석 소요 시간을 단축시키기 위해 기하학적 대칭성을 고려하여 Fig. 2에 표시된 파란색 영역과 같이 전체 형상의 1/4만을 모델링하였다. 이는 구조가 X축과 Y축을 기준으로 대칭성을 갖기 때문에, 각 방향으로 절반씩만 모델링해도 전체 구조 거동을 효과적으로 모사할 수 있기 때문이다. 여기서, X축은 섬유 방향, Y축은 수지 방향, Z축은 적층 방향을 의미한다.
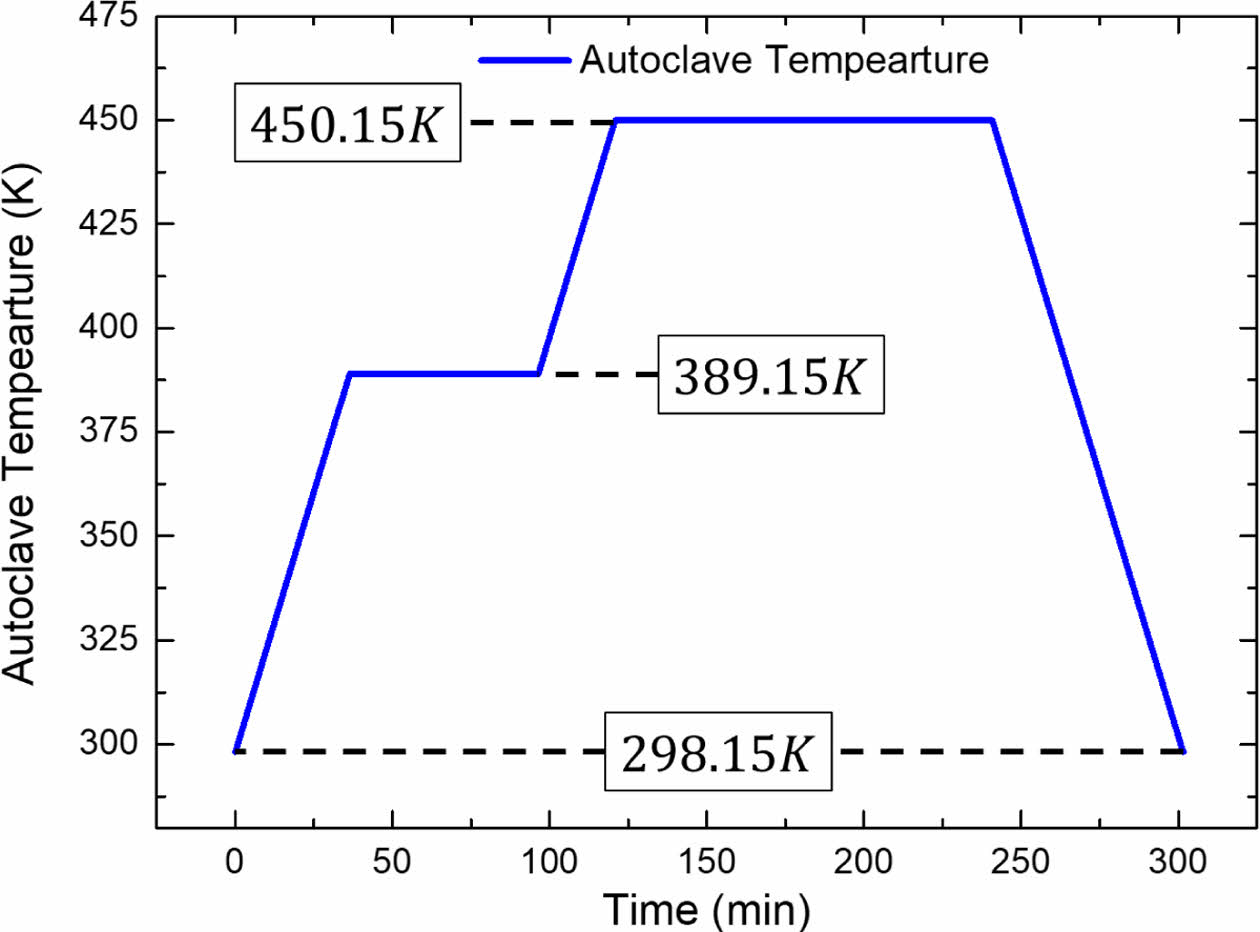
오토클레이브 온도 사이클은 Fig. 3과 같이 제조사 권장 경화 사이클(Manufacturer’s Recommended Cure Cylce, MRCC)을 기반으로 설정하였다. 복합재 표면에 이 사이클을 직접 적용함으로써, 오토클레이브 온도와 복합재 표면 온도가 동일하게 작용하도록 하중조건을 부여하였다.
경계 조건은 실제 성형 공정을 모사하여 설정하였다. 복합재 모델이 몰드에 밀착된 상태를 반영하여, 모델의 바닥면에는 Z축(적층 방향)의 변위를 구속하였다. 또한, 모델의 대칭성을 고려하여 XZ면의 절점에는 Y축(수지 방향)에 대한 대칭 조건을, YZ면의 절점에는 X축(섬유 방향)에 대한 대칭 조건을 각각 적용하였다.
ABAQUS를 활용하여 열-구조 연계 해석을 수행하였으며, 해석에 사용된 요소는 3차원 6면체 요소인 C3D8T를 총 10,000개를 사용하였다. 재료의 물성은 2절의 Table 1-4에 제시된 값과 같으며, 이는 White, Kim[9], Zhang[10]의 유한 요소 해석 모델과 동일한 데이터를 사용하였다.
3.2 유한 요소 해석 모델 검증 결과
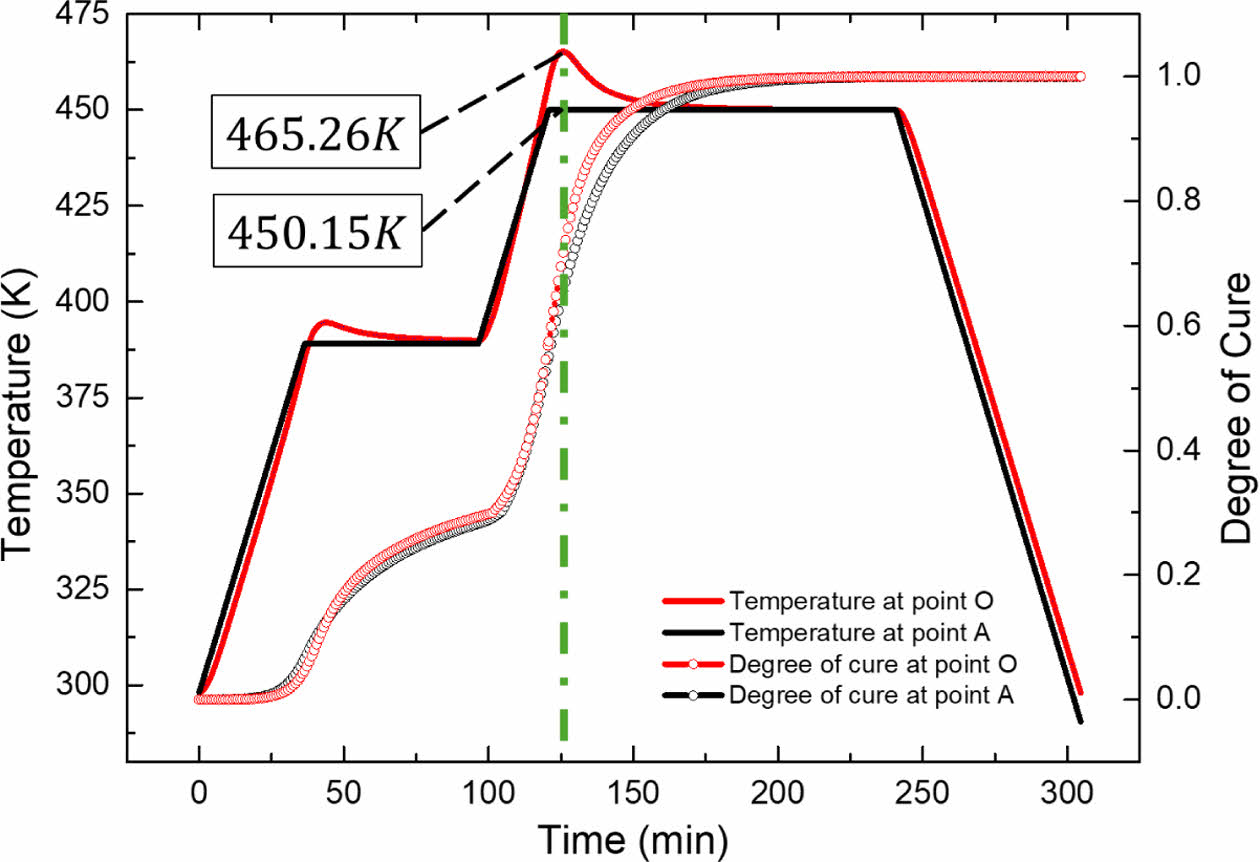
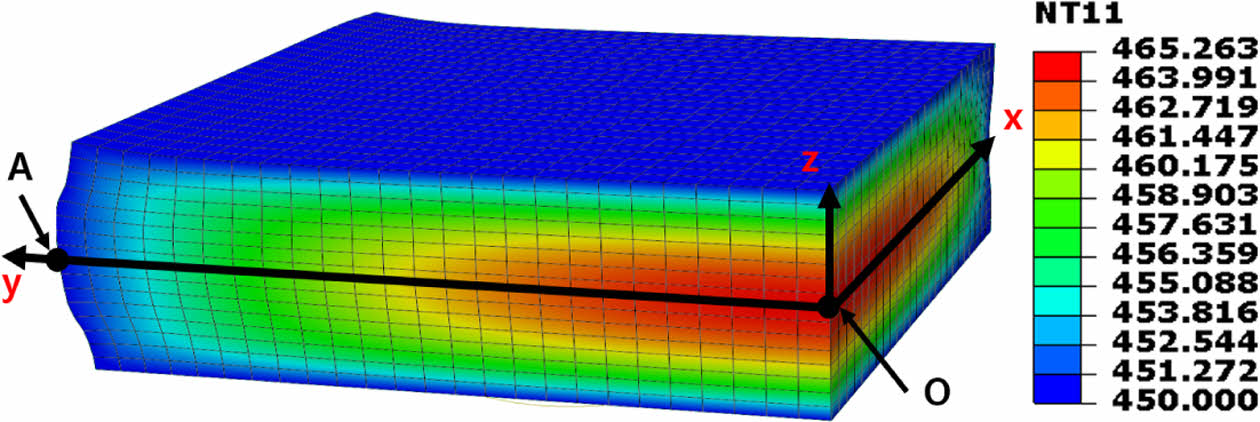
Fig. 4는 본 연구에서 모델링한 오토클레이브 공정의 유한 요소 해석 결과로, Fig. 2에 표시된 복합재 표면부와 중심부에서 시간에 따른 온도 및 경화도의 변화를 나타낸 그래프이다. X축은 성형 시간, 좌측 Y축은 온도, 우측 Y축은 경화도를 나타낸다. A 지점인 표면부와 O 지점인 중심부 간의 온도 차이가 가장 크게 발생하는 시점의 온도는 Fig. 5와 같다.
오토클레이브 온도가 상승하거나 하강하는 구간에서는 복합재의 표면부와 중심부 사이에 온도 차이가 발생하였으며, 이는 열전달 과정에서의 시간 지연에 기인한다. 또한, 온도가 일정하게 유지되는 구간에서도 수지의 화학 반응열로 인해 두 지점 간의 온도 차이는 지속적으로 유지되었다.
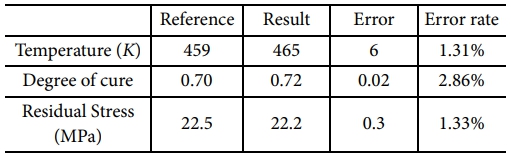
본 연구의 해석 결과는 White, Kim[9]의 연구 결과와 유사한 경향을 보였으며, 특히 두 지점 간의 온도 차가 최대인 125분 시점에서 그 차이가 두드러지게 나타났다. 이 시점에서 White, Kim[9]의 결과는 A 지점인 복합재 표면부의 온도 459 K, 경화도 0.70을 나타냈고, 본 연구의 결과는 온도 465 K, 경화도 0.72로 매우 유사함을 확인하였다.
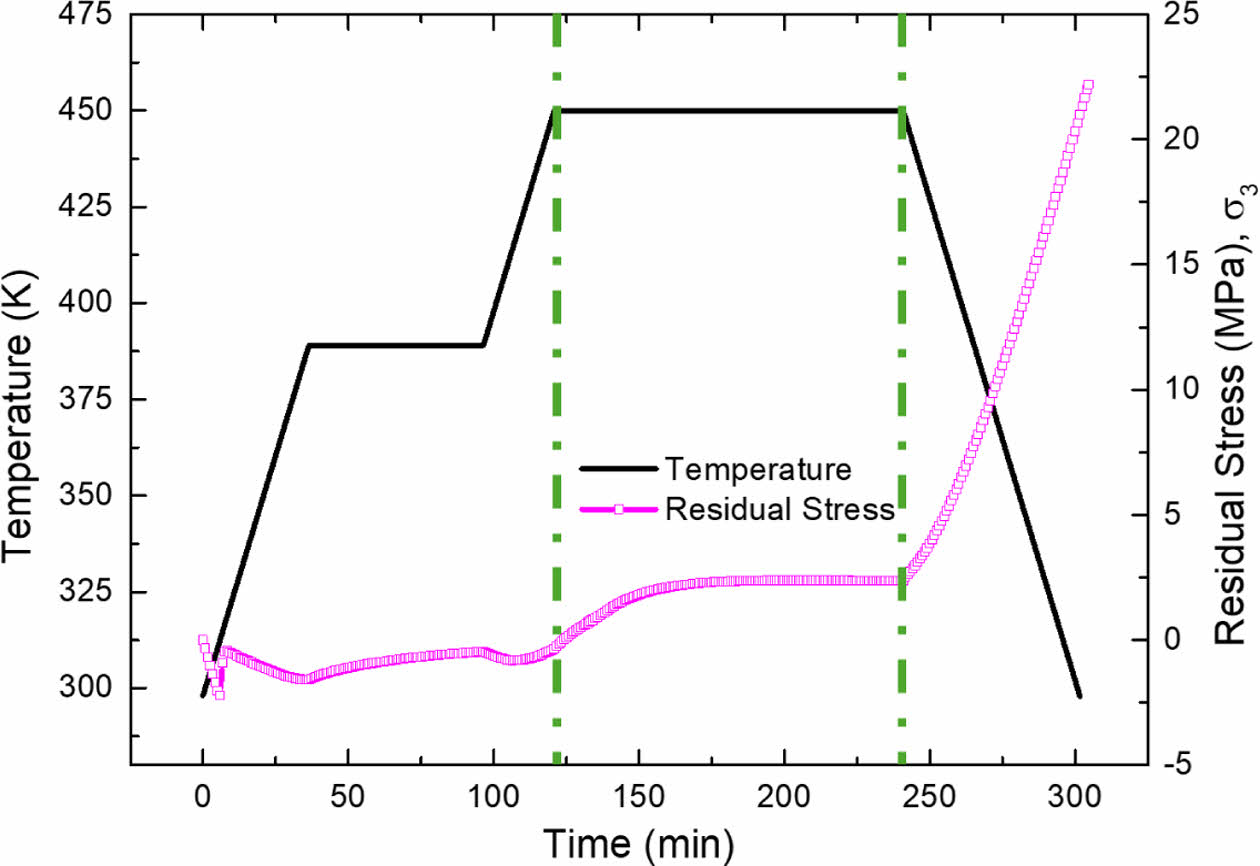
Fig. 6은 오토클레이브 공정 중 A 지점인 표면부에서 시간에 따른 잔류응력 변화를 나타낸 그래프이며, 성형이 완료된 시점의 최종 잔류응력은 Fig. 7과 같다. 이때 X축은 성형 시간, 좌측 Y축은 온도, 우측 Y축은 잔류응력을 나타낸다.
복합재 표면부의 해석 결과에 따르면, 성형 시작 직후 0분부터 5분까지는 수지가 아직 경화되지 않은 유동 상태에 있으며, 이 시점에서는 열팽창계수 차이에 따른 적층 간 변형 불일치로 인해 순간적으로 응력이 발생하고, 수지의 점탄성 특성에 따라 빠르게 완화되는 현상이 나타났다. 이후 5분부터 120분까지는 온도가 상승함에 따라 적층 간 열팽창계수 차이로 인한 열팽창 불일치가 지속적으로 누적되며 압축응력이 발생하였다. 121분부터 240분까지는 수지의 경화가 진행되면서 화학 수축이 발생하고, 이에 따라 인장응력이 증가하면서 기존의 압축응력이 인장응력으로 전환되었다. 241분 이후의 냉각 구간에서는 경화가 완료되어 화학 수축은 발생하지 않지만, 복합재가 냉각되면서 적층 간 열팽창계수 차이에 의해 인장응력이 더욱 증가하였다.
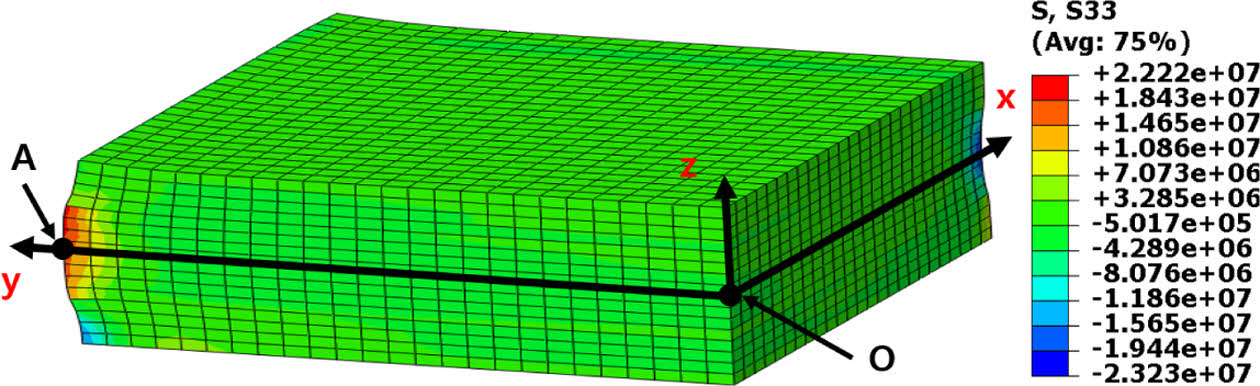
본 연구의 해석 결과는 Zhang[10]의 연구 결과와 유사한 경향을 보였으며, 성형이 완료된 301분 시점에서 Zhang[10] 의 결과는 22.5 MPa를 나타냈고, 본 연구의 결과는 22.2 MPa로 매우 유사함을 확인하였다.
이를 통해 본 연구에서 모델링한 해석 모델의 신뢰성을 검증하였으며, 해석 결과와 선행 연구[9,10] 간의 오차율은 Table 5에 정리하였다.
|
Fig. 2 Geometry of AS4/3501-6 composite |
|
Fig. 3 Temperature cycle of Autoclave |
|
Fig. 4 Temperature & Degree of cure at point A, O (125min) |
|
Fig. 5 Temperature distribution at point A, O (125min) |
|
Fig. 6 Residual stress at point A |
|
Fig. 7 Residual stress distribution at point A (301min) |
4.1 냉각 속도에 따른 유한 요소 해석 모델링
본 연구에서는 3절에서 검증한 유한 요소 해석 모델을 기반으로, 성형 공정 중 경화 완료 이후의 냉각 과정에서 냉각 속도를 변수로 설정하여 잔류응력을 예측하였다. 해석에 사용된 모델은 Fig. 2에 표시된 파란색 영역으로, AS4/3501-6 복합재 평판 형상이다. 적층 배열은 [0°/90°]s, 크기는 50.8 mm × 50.8 mm × 25.4 mm이다.
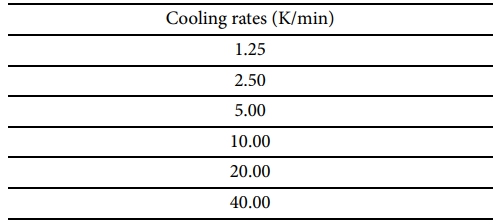
냉각 과정의 시작 온도는 450.15 K, 종료 온도는 298.15 K로 설정하였으며, 총 6가지 냉각 속도 조건으로 구성하여 Table 6에 정리하였다.
하중 조건은 오토클레이브 온도 사이클 중 냉각 구간을 제외한 모든 구간에서 동일하게 적용하였고, 냉각 구간에서는 조건별로 냉각 속도만 다르게 설정하여 해석을 수행하였다. 경계 조건과 재료의 물성치는 앞서 수행한 해석 검증과 동일하게 설정하였다.
냉각 속도 제어는 ABAQUS USER SUBROUTINE 중 DISP 서브루틴을 활용하여 구현하였다. 코드 내에서 시간에 따른 냉각 속도 파라미터를 수정하여 각 조건을 반영하였으며, 오토클레이브 온도 사이클의 5개 주요 구간 중 마지막 냉각 구간에서만 냉각 속도를 변경함으로써 모든 조건에서 동일한 온도 사이클을 유지하면서도 냉각 속도만 제어할 수 있도록 구성하였다.
4.2 냉각 속도에 따른 유한 요소 해석 결과
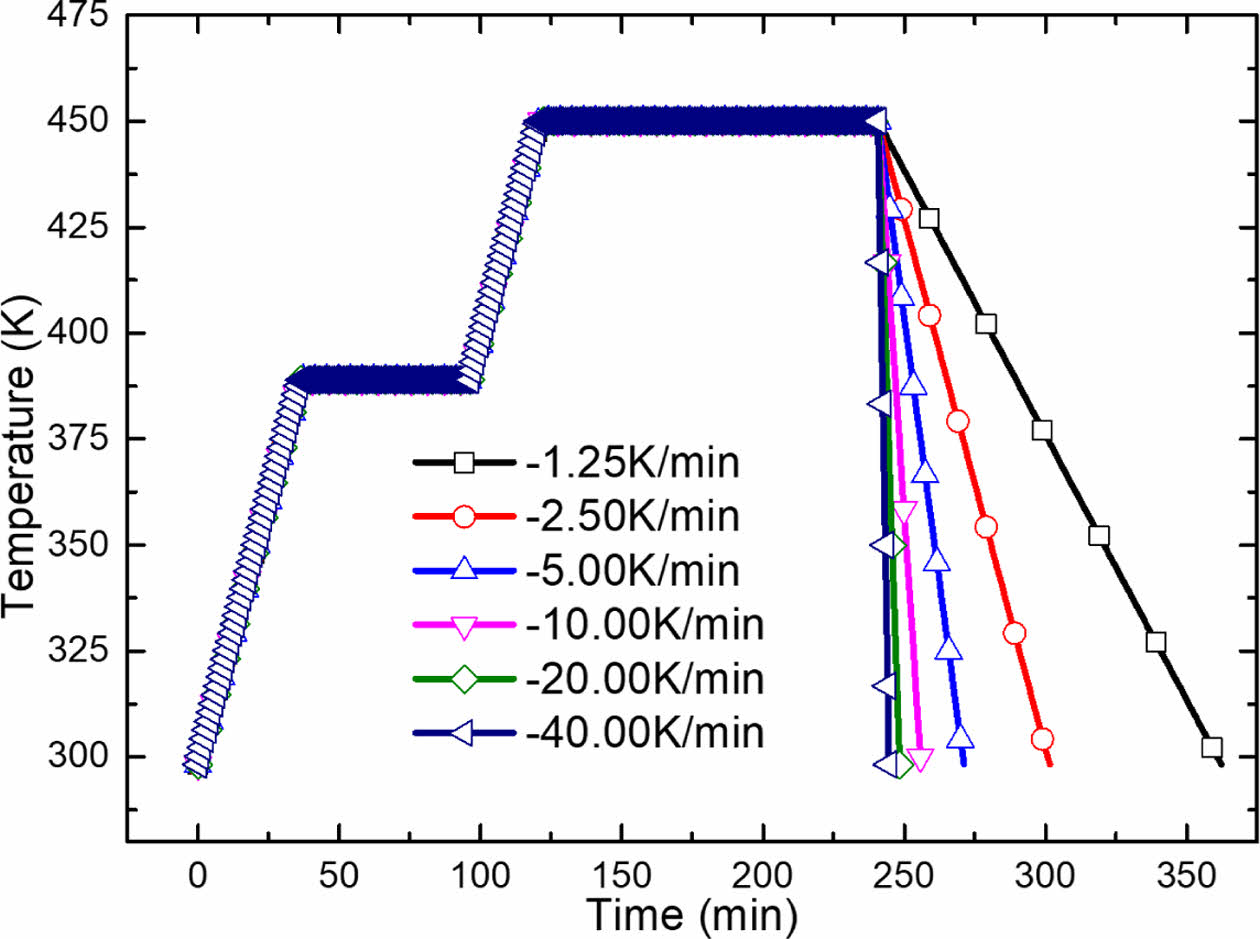
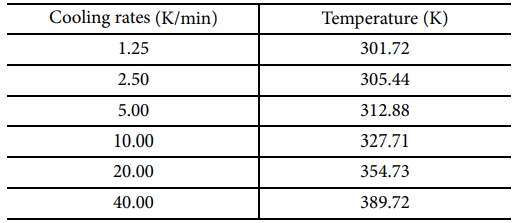
각 냉각 속도 케이스에 대해 복합재 표면부인 A 지점과 중심부인 O 지점에서 발생하는 잔류응력을 비교 및 분석하였다. Table 6에 제시된 냉각 속도 조건을 적용하여 수행한 유한 요소 해석 결과, 냉각 종료 시점에서 표면부의 온도는 Fig. 8과 같이 오토클레이브 온도와 동일한 298.15 K까지 냉각이 완료된 것으로 나타났다. 반면, Fig. 9에서 확인할 수 있듯이 복합재 중심부는 동일한 시간 내에 298.15 K에 도달하지 못하고 더 높은 온도를 유지하고 있었다.
복합재 중심부의 최종 온도는 냉각 속도에 따라 301.72 K에서 389.72 K까지 다양하게 나타났으며, 해당 결과는 Table 7에 정리하였다. 이를 바탕으로 중심부의 온도가 298.15 K에 도달하기까지 필요한 잔여 온도차를 각 케이스의 냉각 속도로 계산한 결과, 모든 조건에서 약 2.7분의 추가 냉각 시간이 소요되는 것으로 확인하였다.
냉각 속도가 증가할수록 복합재의 표면부에서는 인장응력이, 중심부에서는 압축응력이 증가하는 경향을 보였다. 이는 섬유와 수지 간의 열팽창계수 차이로 인해 냉각 과정 중 온도 변화에 따른 수축률이 서로 다르기 때문이며[8], 이로 인해 표면과 중심 간 응력 차이가 발생하게 된다.
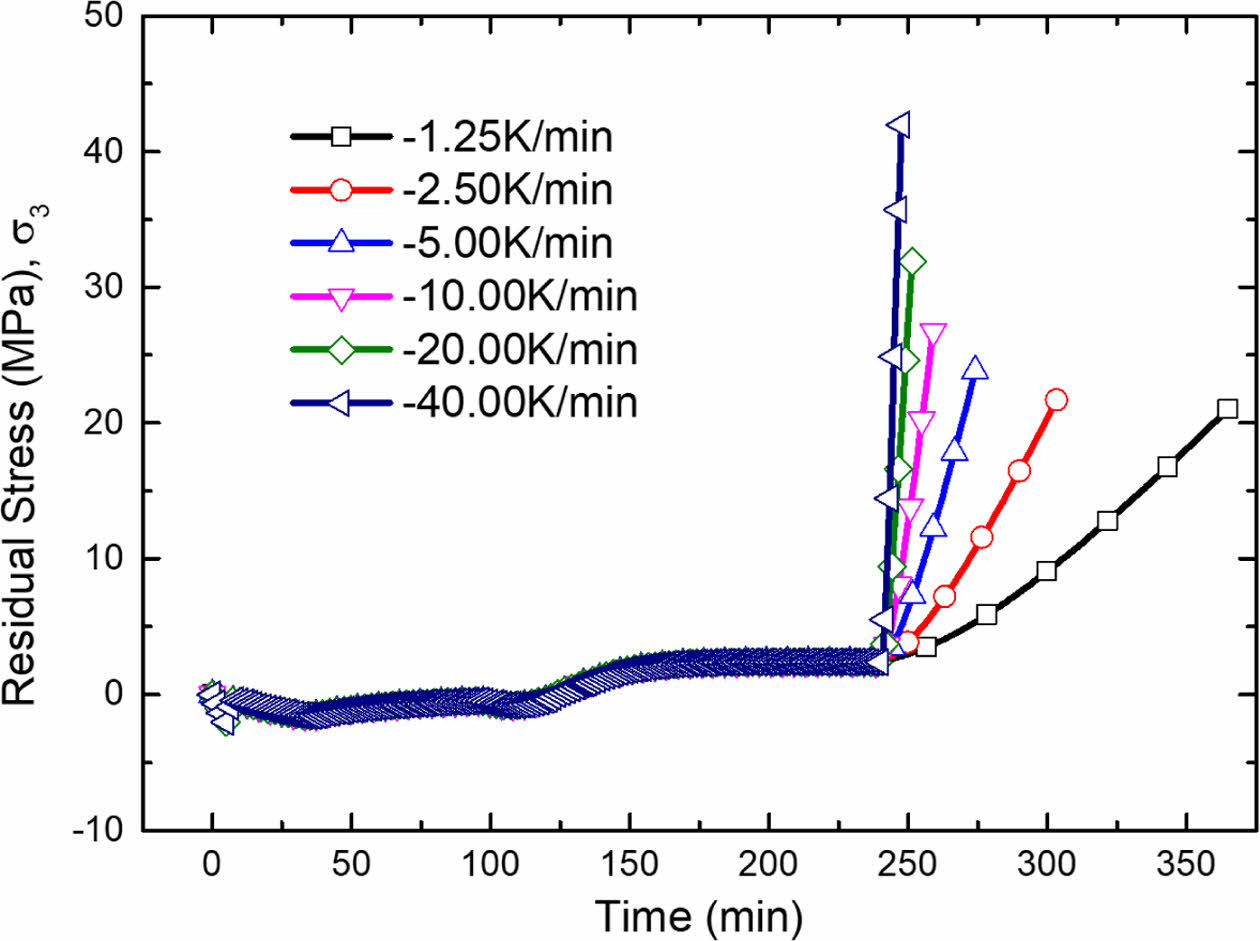
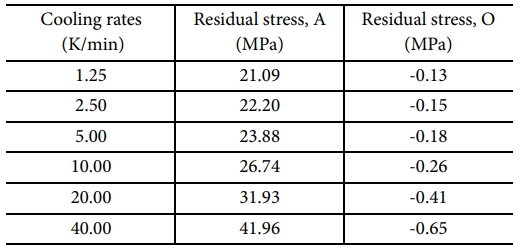
Fig. 10에 따르면, 냉각이 시작되는 241분 이후부터 표면부에서 인장응력이 점차 증가하기 시작하였다. 냉각 속도1.25 K/min 및 2.50 K/min 조건에서는 인장응력이 비교적 완만하게 증가하는 경향을 보였으며, 이는 수지의 점탄성 거동으로 인해 응력이 시간에 따라 점진적으로 완화되는 특성이 반영된 결과이다. 반면, 5.00 K/min 이상의 고속 냉각 조건에서는 인장응력이 선형적으로 급격히 증가하였으며, 시간에 따른 응력 완화는 거의 발생하지 않았다. 이는 냉각 속도가 빠를수록 응력을 완화할 수 있는 충분한 시간적 여유를 확보하지 못했기 때문이다. 결과적으로, 냉각 속도 40.00 K/min 조건에서 최대 인장 잔류응력은 41.96 MPa로 발생했으며, 이는 1.25 K/min 조건에서의 21.09 MPa 대비 약 2배 높은 수치이다.
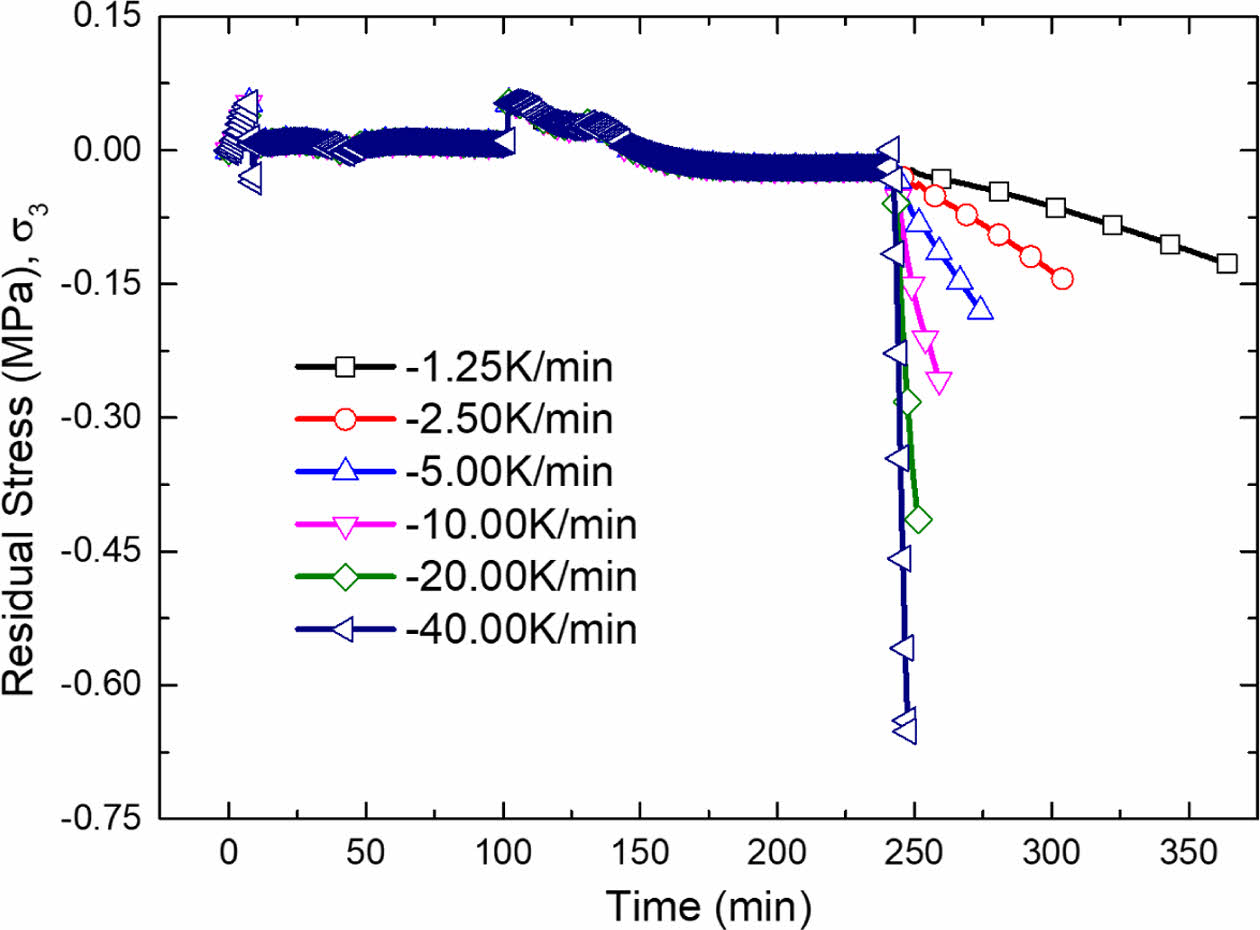
Fig. 11은 복합재 표면부인 O 지점에서 시간에 따른 잔류응력 변화를 나타낸다. 모든 조건에서 압축응력이 발생하였으며, 냉각 속도가 증가할수록 압축응력 또한 증가하는 경향을 보였다. 냉각 속도 1.25 K/min 및 2.50 K/min 조건에서는 압축응력이 비교적 완만하게 증가하였고, 5.00 K/min 이상의 고속 냉각 조건에서는 급격한 증가를 보였다. 이는 복합재 표면부에서의 온도 하강 속도가 중심부보다 느리고, 수축 속도 또한 낮아 점탄성에 의한 응력 완화가 상대적으로 제한적으로 발생한 결과로 해석된다. 가장 빠른 냉각 조건에서의 최대 압축 잔류응력이 -0.65 MPa로 나타났다.
또한, 표면부와 중심부 간의 응력 차이는 냉각 속도에 따라 뚜렷하게 확대되었다. 저속 냉각 조건에서는 두 지점 간의 잔류응력 차이가 비교적 작았으나, 고속 냉각 조건에서는 표면부의 인장응력과 중심부의 압축응력 간의 차이가 최대 42.61 MPa에 달하였다. 이러한 응력 불균형은 치수 오차 및 뒤틀림(Warpage), 기계적 성능 저하와 같은 구조적 손상을 유발할 수 있는 주요 요인으로 작용할 수 있다. 본 연구에서 수행한 냉각 속도 조건별 유한 요소 해석 결과는 Table 8에 정리하였다.
|
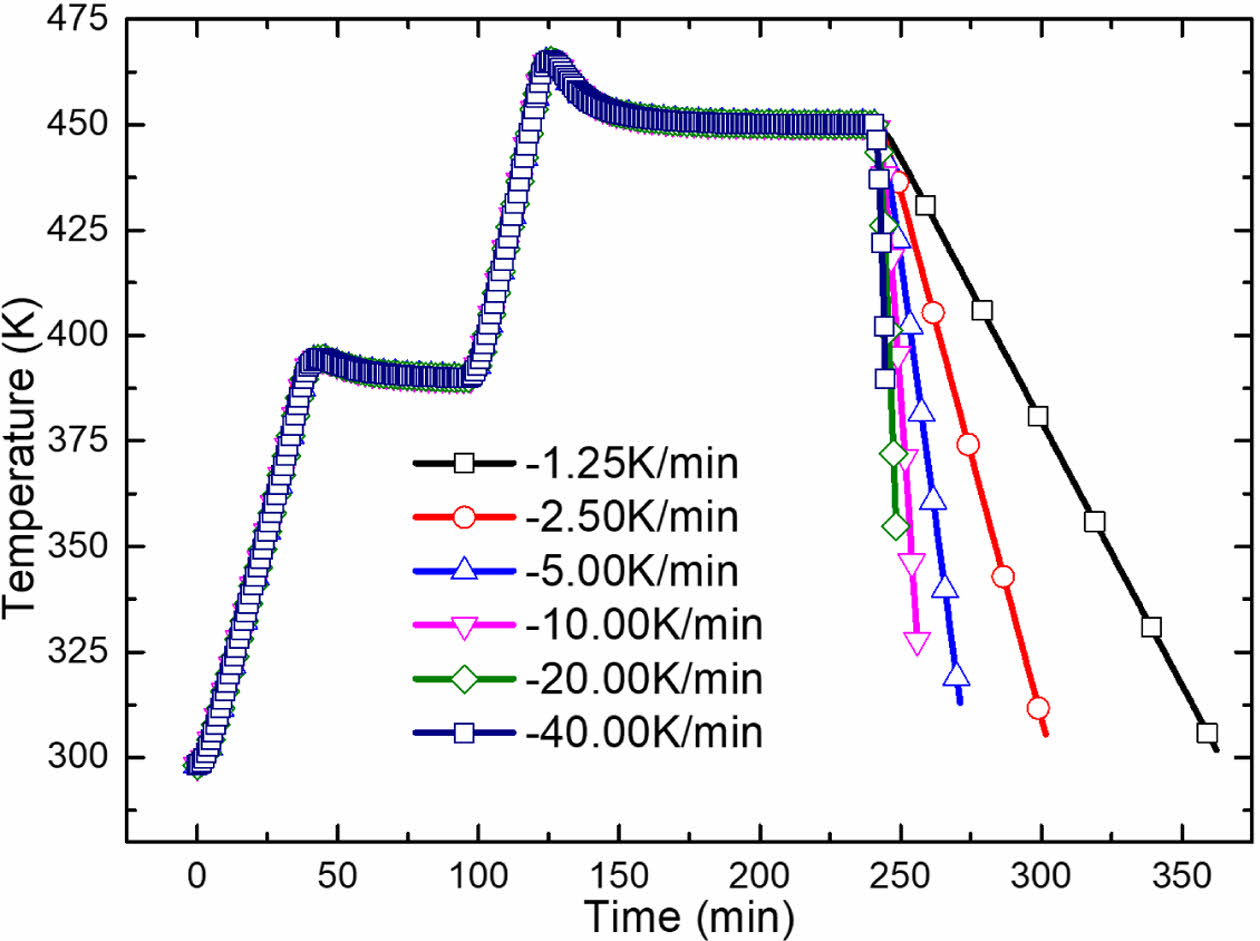
Fig. 8 Temperature variation at point A for different cooling rates |
|
Fig. 9 Temperature variation at point O for different cooling rates |
|
Fig. 10 Residual stress at point A by different cooling rates |
|
Fig. 11 Residual stress at point O by different cooling rates |
본 연구에서는 오토클레이브를 사용하는 열경화성 복합재 성형 공정에서 발생하는 잔류응력을 예측하고, 냉각 속도 변화가 잔류응력에 미치는 영향을 분석하기 위해 유한 요소 해석을 수행하였다. 이를 위해 ABAQUS와 ABAQUS USER SUBROUTINE을 활용하여, 수지의 점탄성 거동과 화학 반응열을 고려한 열-구조 연계 해석 모델을 구현하였다.
유한 요소 해석 기법의 신뢰성을 검증하기 위해 White, Kim[9], Zhang[10]의 선행 연구와 동일한 해석 조건을 적용하여 비교 검증을 수행하였으며, 복합재 표면부인 A 지점과 중심부인 O 지점의 온도, 경화도, 잔류응력 결과는 최대 2.86% 이내의 오차율로 유사한 경향을 나타내어 해석 기법의 신뢰성을 확인하였다.
이후, 냉각 속도를 변수로 설정하여 총 6가지 조건에 대해 잔류응력을 예측하였다. 그 결과, 냉각 속도에 따라 수지의 점탄성 거동에 영향을 미치는 것으로 확인되었으며, 저속 냉각에서는 응력이 부분적으로 완화되었으나, 고속 냉각에서는 응력 완화가 거의 이루어지지 않아 잔류응력이 크게 증가하여 잔류응력의 불균형이 뚜렷하게 나타났다. 또한, 냉각 속도가 증가할수록 표면부에서는 인장응력이, 중심부에서는 압축응력이 각각 증가하는 경향을 보였으며, 두 지점 간의 최대 응력 차이는 최대 42.61 MPa로 나타났다. 이러한 결과는 냉각 과정에서의 열전달 지연으로 인해 복합재 중심부가 표면부보다 늦게 냉각되기 때문이다. 먼저 냉각된 표면부는 온도 저하로 인해 수축하려는 반면, 중심부는 고온 상태를 유지하며 팽창되어 있는 상태이기 때문에 표면부의 수축이 제한되어 인장응력이 발생하고, 중심부는 냉각 초기에 고온 상태로 팽창되어 있으며, 이로 인해 표면부의 수축이 제한되면서 인장응력이 발생한다. 이후 시간이 경과함에 따라 중심부도 점차 냉각되어 수축하려 하지만, 이미 수축된 표면부가 이를 구속하여 압축응력이 발생하게 된다.
이러한 현상은 복합재 내부의 온도 차이에 의해 발생한 응력 불균형에 기인하며, 이로 인한 열기계적 상호작용이 복합재 내부 응력 분포에 중요한 영향을 미친다는 것을 시사한다.
따라서, 냉각 속도는 복합재 성형 공정에서 잔류응력 제어 및 제품 품질 확보에 있어 핵심적인 공정 변수임을 확인할 수 있었으며, 본 연구에서 구현한 유한 요소 해석 기법은 향후 다양한 적층 배열 및 형상을 갖는 복합재 성형 공정에 적용 가능한 해석 기반 기법으로 확장될 수 있을 것으로 기대된다.
본 연구는 부산대학교 기본연구지원사업(2년) 및 정부 (과학기술정보통신부)의 재원으로 우주항공청 미래우주교육센터(RS-2022-NR067081)의 지원을 받아 수행된 것이며, 지원에 대해 진심으로 감사드립니다.
- 1. Mrazova, M., “Advanced Composite Materials of the Future in Aerospace Industry,” Incas Bulletin, Vol. 5, No. 3, 2013, pp. 139-150.
-

- 2. Baran, I., Cinar, K., Ersoy, N., Akkerman, R., and Hattel, J. H., “A Review on the Mechanical Modeling of Composite Manufacturing Processes,” Archives of Computational Methods in Engineering, Vol. 24, 2017, pp. 365-395.
-

- 3. Jung, S. R., Kim, W. D., and Kim, J. H., “Analysis of Thermal Deformation of Carbon-fiber Reinforced Polymer Matrix Composite Considering Viscoelasticity,” Journal of the Korean Society for Composite Materials, Vol. 27, No. 4, 2014, pp. 174-181.
-

- 4. Seong, D. Y., and Kim, W. D., “Thermal Deformation Analysis of L-shaped Composite During Cure Process by Viscoelastic Model,” Journal of the Korean Society for Composite Materials, Vol. 33, No. 4, 2020, pp. 220-227.
- 5. Lee, H. J., and Kim, W. D., “Residual Deformation Analysis of Composite by 3-D Viscoelastic Model Considering Mold Effect,” Journal of the Korean Society for Composite Materials, Vol. 34, No. 6, 2021, pp. 426-433.
- 6. Yu, J. W., and Kim, W. D., “Prediction of Temperature and Degree of Cure of Carbon Fiber Composites Considering Thermal Chemical Reaction,” Journal of the Korean Society for Composite Materials, Vol. 36, No. 5, 2023, pp. 315-320.
- 7. Gang, J. H., and Kim, S. D., “Finite Element Analysis of an Epoxy Curing Processes by using Abaqus User Subroutine,” Computational Structural Engineering, Vol. 28, No. 4, 2015, pp. 7-11.
- 8. Kim, Y. K., and White, S. R., “Viscoelastic Analysis of Processing-induced Residual Stresses in Thick Composite Laminates,” Mechanics of Composite Materials and Structures an International Journal, Vol. 4, No. 4, 1997, pp. 361-387.
-

- 9. Zhang, J. T., Zhang, M., Li, S. X., Pavier, M. J., and Smith, D. J., “Residual Stresses Created during Curing of a Polymer Matrix Composite Using a Viscoelastic Model,” Composites Science and Technology, Vol. 130, 2016, pp. 20-27.
-

- 10. Lee, W. I., Loos, A. C., and Springer, G. S., “Heat of Reaction, Degree of Cure, and Viscosity of Hercules 3501-6 Resin,” Journal of Composite Materials, Vol. 16, No. 6, 1982, pp. 510-520.
-

- 11. Hou, J., You, B., Xu, J., Fu, T., and Wang, T., “Numerical Simulation and Multi-objective Optimization for Curing Process of Thermosetting Prepreg,” Applied Composite Materials, Vol. 29, No. 4, 2022, pp. 1409-1429.
-

- 12. Kim, Y. K., Process-induced Viscoelastic Residual Stress Analysis of Graphite/epoxy Composite Structures, Ph. D Thesis, University of Illinois at Urbana-Champaign, 1996.
 This Article
This Article
-
2025; 38(5): 553-561
Published on Oct 31, 2025
- 10.7234/composres.2025.38.5.553
- Received on Apr 2, 2025
- Revised on Apr 15, 2025
- Accepted on May 16, 2025
 Services
Services
Shared
 Correspondence to
Correspondence to
- Wie-Dae Kim
-
Department of Aerospace Engineering, Pusan National University
- E-mail: wdkim@pusan.ac.kr






 Copyright ⓒ The Korean Society for Composite Materials. All rights reserved.
Copyright ⓒ The Korean Society for Composite Materials. All rights reserved.