- Quantum Annealing-Based Stacking Sequence Optimization and Impact Performance Evaluation of Natural Hybrid Composites
S. Cho*, Cheol Min Shin**, Hyun Woo Kim**, Sang Deok Kim**, Chung Woo Park**, Seong S. Cheon*†
* Department of Mechanical Engineering, Graduated School, Kongju National University
** Kwangsung Corporation LTD- 양자 어닐링 기반 적층 순서 최적화 및 천연 하이브리드 복합재의 충격 성능 평가
조성욱* · 신철민** · 김현우** · 김상덕** · 박충우** · 전성식*†
This article is an open access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Natural hybrid composites are considered promising alternatives to conventional synthetic composites due to their eco-friendliness, light weight, and low cost. In this study, quantum annealing (QA) was applied as a strategy to maximize the impact energy absorption performance of such composites. The stacking sequence optimization was performed on 114 variables derived from the combinations of six natural fibers (Bamboo, Flax, Hemp, Ramie, Jute, and Kenaf) and 19 fiber orientation angles. The bending characteristics of each combination were evaluated through radius of curvature analysis based on classical laminate theory, and the resulting values were used as indicators of deformation resistance under impact loading. The objective function was reformulated into a Quadratic Unconstrained Binary Optimization (QUBO) model and embedded into a quantum annealer. QA-based combinatorial optimization was conducted under specific gravity and cost constraints, and the resulting stacking configurations were evaluated through Charpy impact simulation. The analysis revealed that combination D, in which Ramie and Jute fibers were complementarily stacked, achieved the highest impact energy absorption.
천연 하이브리드 복합재는 친환경성, 경량성, 저비용 등의 장점으로 인해 기존 합성 복합재를 대체할 수 있는 유망한 소재로 간주되고 있다. 본 연구에서는 이러한 복합재의 충격 흡수 성능을 극대화하기 위한 방안으로 양자 어닐링(Quantum Annealing, QA)이 적용되었다. 적층 순서의 최적화는 6종의 천연섬유(Bamboo, Flax, Hemp, Ramie, Jute, Kenaf)와 19가지 섬유 각도의 조합으로 구성된 총 114개의 변수에 대해 수행되었으며, 각 조합의 굽힘 특성은 고전 적층판 이론에 기반한 곡률 반경 분석을 통해 산정되었다. 이 곡률 반경은 충격 하중 하에서의 변형 저항성을 반영하는 지표로 활용되었으며, 목적함수는 QUBO(Quadratic Unconstrained Binary Optimization) 형태로 변환되어 양자 어닐러에 임베딩되었다. 비중 및 비용에 대한 제약 조건이 반영된 QA 기반의 조합 최적화가 수행되었고, 도출된 적층 조합은 샤르피 충격 해석을 통해 평가되었다. 분석 결과, Ramie와 Jute 섬유가 상호보완적으로 적층된 조합 D에서 가장 높은 충격 흡수 에너지가 기록되었다.
Keywords: 양자 어닐링(Quantum annealing), 천연 하이브리드 복합재(Natural hybrid composite), 조합 최적화(Combinatorial optimization), 이진 이차 모델(Binary quadratic model), 샤르피 시험(Charpy test)
천연섬유복합재는 자동차, 항공우주 등 산업 분야에서 친환경적이고 가벼우며 비용 효율적인 소재에 대한 수요가 증가함에 따라 각광받고 있는 복합소재 중 하나이다. 특히 CO2 중립성, 생분해성, 재활용 가능성은 천연섬유복합재의 대표적인 장점으로 여겨지며, 자동차 분야에서 연평균 20% 이상의 성장률로 빠르게 성장하고 있다[1-3]. 이처럼 천연섬유 복합재의 물리적, 기계적 열적 특성을 파악하는데 많은 연구가 진행되고 있으며, 대표적으로 아마(Flax), 대마(Hemp), 황마(Jute), 저마(Ramie), 양마(Kenaf), 그리고 대나무(Bamboo)와 같은 식물 섬유가 기존의 합성섬유의 대체제로써 적용 및 개발되고 있다[4–6]. 그러나 천연섬유복합재의 기계적 거동은 사용된 섬유의 종류, 섬유 부피 분율, 그리고 적층 순서에 따라 크게 달라지게 된다. 특히 적층 순서는 충격과 같은 동적 하중 하에서 이방성 기계적 거동을 정의하는 데 중요한 역할을 한다. 또한 기존 연구에 따르면, 단일 천연섬유 복합재는 기계적 성능에 한계가 있으며, 이를 극복하기 위한 다중 섬유 기반 하이브리드 복합재의 개발이 요구된다[7,8]. 앞선 연구 결과들은 단일 천연섬유복합재의 기계적 성능 한계를 극복하기 위해 합성섬유와의 혼용 또는 두개 이상의 식물섬유로 적층된 하이브리드 형태의 섬유강화복합재에 대한 연구가 필수적임을 시사한다[9–12]. 하이브리드 복합재의 경우 적층 순서를 최적화하는 기존의 접근 방식은 다양한 섬유 종류와 각도로 생성될 수 있는 무수히 많은 조합이 제시되어질 수 있으며, 실험을 통해 전체 조합에서 최적해를 도출하는 것은 많은 시간과 비용이 소요되기에 실제 적용해볼 수 있는 하이브리드 복합재의 가용 조합은 제한적일 수밖에 없다. 또한 설계 변수가 다양해짐에 따라 조합 수는 기하급수적으로 증가하게 되며, 이러한 대규모 전역 영역에서 머신러닝 또는 최적화 알고리즘만으로는 효율적으로 최적해에 수렴하기 어렵다[13]. 앞선 대규모 전역 영역에서의 조합 최적화는 양자 컴퓨터를 적용하여 효율적으로 최적해를 도출할 수 있는데, 양자 터널링 현상을 활용한 양자 어닐링(Quantum annealing, QA) 기법은 대규모 조합 최적화 문제를 짧은 시간안에 해결할 수 있게 해준다[14,15]. 양자 어닐링을 적용하기 위해서는 양자 컴퓨터인 양자 어닐러(Quantum annealer)에 최적화하고자 하는 문제를 임베딩해야 하며, 조합 최적화 문제의 목적함수가 2차 비제약 이진 최적화(Quadratic unconstrained binary optimization, QUBO) 형태로 변환되어 적용되게 된다.
본 연구에서는 천연 하이브리드 복합재의 충격 흡수 에너지가 우수하면서 제한된 비중과 비용 조건을 동시에 만족하는 적층 순서를 QA를 통해 효율적으로 도출하고 도출된 천연 하이브리드 복합재의 충격 특성을 평가하고자 한다. 서로 다른 섬유 재질과 각도로 적층된 하이브리드 복합재 형태는 샤르피 충격 시 발생되는 동적 하중에 대해 각 플라이의 기여도가 상이하다. 샤르피 충격 초기에는 주로 굽힘 변형이 발생하므로, 본 연구에서는 충격 하중에 대한 변형 기여도를 나타내는 지표로써 순수 굽힘 상태에서 각 플라이에 위치한 특정 섬유각도를 나타내는 천연섬유 복합재의 곡률 반경이 QUBO 정의 시 목적함수에서 가중치 항으로 활용된다. 변수로는 섬유의 종류와 각도가 고려되며, 두 변수는 짝을 이루어 하나의 이진 변수로 표현되게 된다. 비중과 비용은 제약조건으로 정의되며, 전체 하이브리드 복합재의 곡률 반경 가중치의 합을 최소화하는 목적함수가 정의되게 된다. 최종적으로 변환된 QUBO는 QA를 통해 조합 최적화가 수행되며, 이를 통해 도출된 적층 조합의 충격 특성은 유한요소해석을 활용한 샤르피 충격 시뮬레이션을 통해 평가된다.
2.1 천연섬유 복합재의 물성
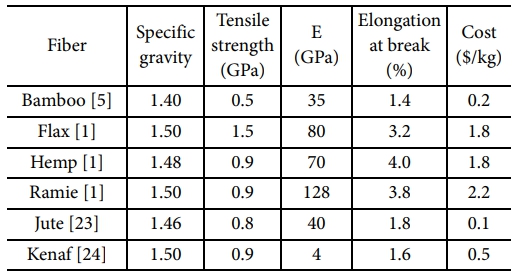
섬유에는 천연섬유와 합성섬유 두가지 유형이 존재하며, 자연에서 나오는 모든 섬유는 주로 동물, 식물 및 광물 세 가지 주요 공급원으로 나뉜다. 이 중 식물성 섬유와 같은 천연섬유는 식물성 식물의 다양한 부분에서 얻어지며 자연에서 제공된다. 본 연구에서는 천연섬유기반 하이브리드 복합재의 기계적 물성치를 조합최적화 문제에 적용하기 위해 기계적 특성이 유효하며 현재 자동차 산업분야에서 활용되고 있는 대표적인 6가지(Bamboo, Flax, Hemp, Ramie, Jute, Kenaf) 식물성 천연섬유가 선정되었으며[16–18], 각 천연섬유의 비중, 단일 섬유에 대한 기계적 특성(인장강도, 탄성계수, 파단 연신율)과 중량에 따른 비용은 Table 1과 같다. 또한 천연섬유 복합재의 기지재로는 일반적으로 사용되는 열경화성 수지인 epoxy resin이 선정되었으며[19–22], 해당 기계적 물성 정보는 Table 2와 같다.
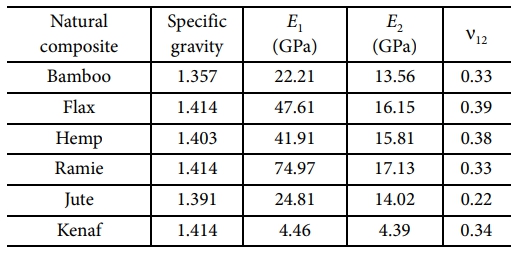
앞서 소개된 Table 1과 Table 2에서의 천연섬유 후보군과 기지재의 기계적 물성은 혼합물 법칙을 통해 각 천연섬유를 강화재로 하는 천연섬유 복합재의 기계적 물성을 도출하는데 사용되며, 다음 식 (1a)을 통해 계산되어진다[26].
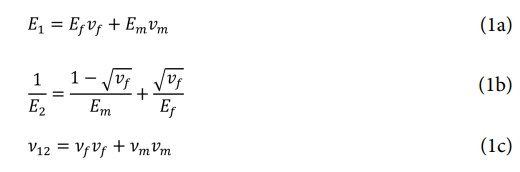
여기서 E1과 E2는 각각 종탄성계수와 횡탄성계수를 의미하며, Ef 와 Em는 섬유와 수지의 탄성계수를 나타낸다. νf 와 νm은 각각 섬유와 수지의 부피분율을 의미하며, 본 연구에서는 천연섬유의 부피분율은 0.57로 선정되었다[25]. 주 푸아송 비인 ν12는 섬유와 수지의 푸아송 비를 나타내는 νf 와 νm에 각각 νf 와 νm이 곱해져 계산되며, 식 (1a)을 통해 계산된 각 천연섬유복합재의 기계적 물성은 Table 3과 같다.
2.2 플라이별 곡률 반경에 따른 가중치 정의
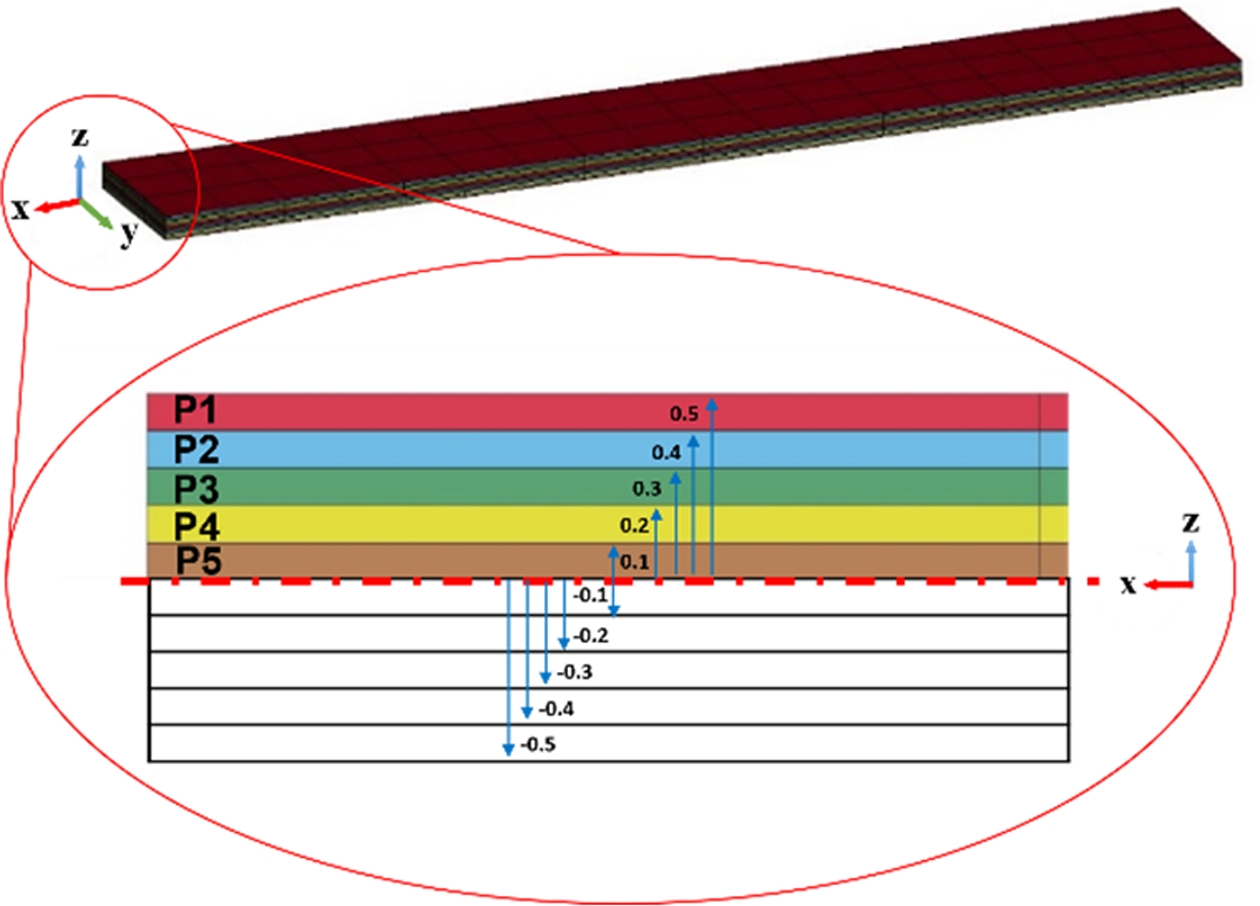
곡률 반경을 계산하고자 하는 복합재는 Fig. 1과 같이 두께 0.1 mm인 플라이 10장이 모두 90o로 적층 된 구조이며, 중심면을 기준으로 대칭이다. 각 플라이에서의 섬유 각도는 0o~ 90o 범위내에서 5o 간격으로 총 19가지의 각도가 적용될 수 있으며, 적층 순서에 따른 천연섬유별 고유 굽힘 하중 특성을 곡률 반경으로 표현하기 위해 전체 복합재는 하나의 천연섬유로만 구성된다.
P1부터 P5에 적용될 수 있는 19가지의 섬유 각도와 6가지의 천연섬유 후보군은 적층 조합 최적화에 대한 목적함수로 적용될 수 있는 114개의 가중치 항으로 나타낼 수 있으며, 고전 적층판 이론에 따라 순수 굽힘 상태로 가정된 복합재의 모멘트-곡률 관계식을 통해 곡률 반경이 도출되었다[27].
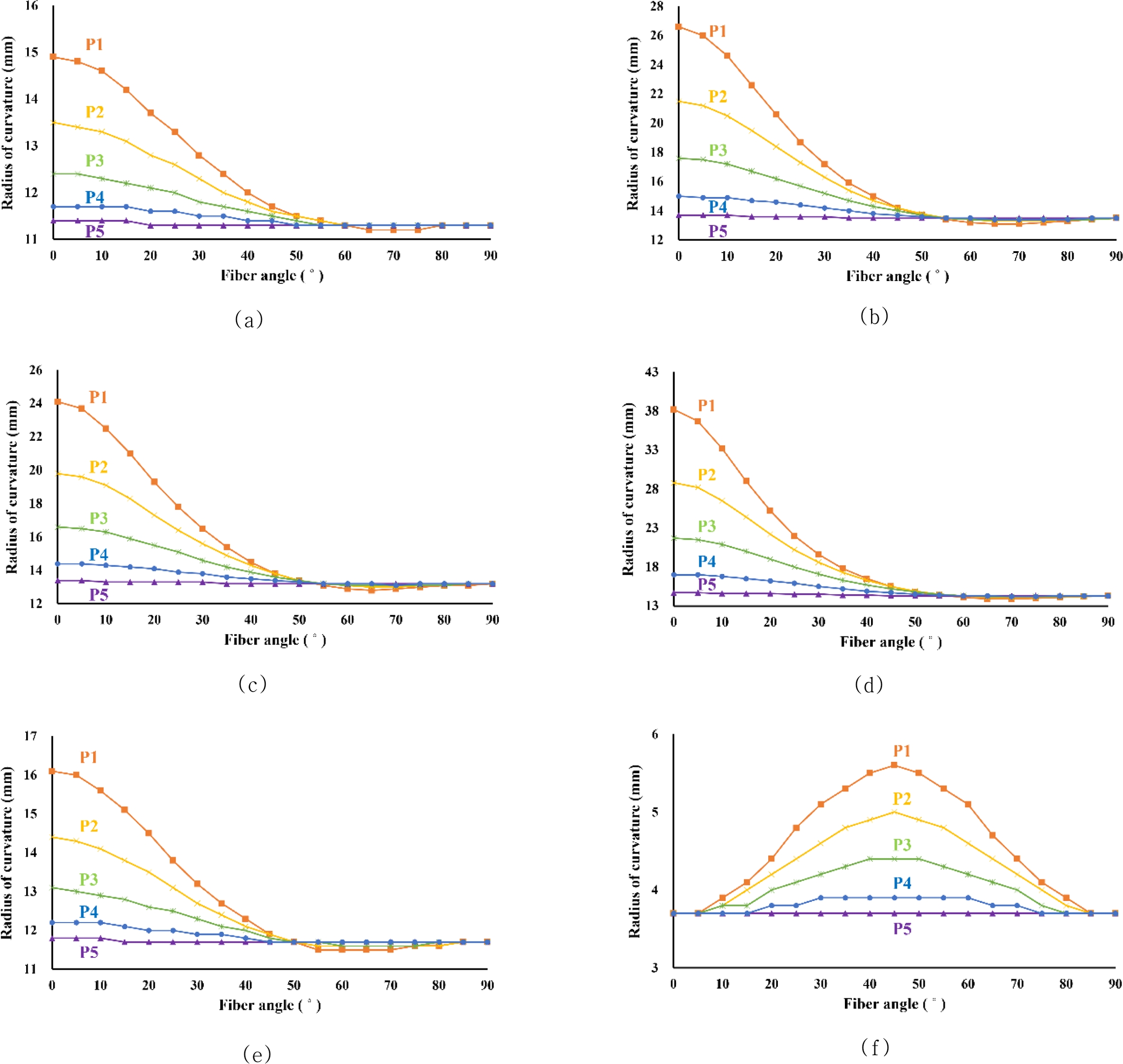
Fig. 2는 섬유각도에 따른 곡률반경을 P1에서 P5의 적층 순서에 따라 Table 3에서의 천연섬유 종류 별로 도출된 결과이다. Fig. 2(a)-(e)는 각각 Bamboo, Flax, Hemp, Ramie, Jute에 대한 결과이다. 5가지 섬유 위치 중 중심면에서 가장 멀리 위치한 P1에서 곡률 반경이 가장 크게 나타났으며, 섬유각도의 증가에 따라 곡률 반경의 변화도 가장 크게 관찰되었다. 이는 P1에서 굽힘 하중에 의한 변형 저항성이 섬유 각도에 매우 민감하게 반응함을 시사한다. 반면, 중심면에 가장 가까운 P5에서는 곡률 반경이 가장 작게 나타났고, 섬유각도의 증가에 따른 곡률 반경의 변화 또한 가장 작았다. 이러한 결과는 P5의 위치에서는 굽힘 하중에 의한 구조 응답이 비교적 안정적이며, 섬유 각도 변화에 따른 변형 특성의 민감도가 낮음을 의미한다. Fig. 2(f)의 Kenaf의 경우 다른 5가지 섬유와 다르게 섬유각도에 따른 곡률 반경의 변화 양상이 다르게 나타난 것을 볼 수 있으며, 이는 Table 3의 Kenaf 결과에서 E1(4.46 GPa)과 E2(4.39 GPa)가 거의 동일하게 나타난 것에 기반한 등방성 특성에 기인한 것으로 사료되어진다. 전체적으로 볼 때, 곡률 반경의 크기 및 민감도는 섬유의 종류, 적층 순서 및 각도에 따라 달라지며, 이는 복합재의 충격 에너지 흡수 성능을 결정짓는 중요한 요소로 작용될 수 있다.
|
Fig. 1 Stacking sequence of natural hybrid composite |
|
Fig. 2 Radius of curvature for each natural fiber according to fiber angle in each ply: (a) Bamboo/epoxy, (b) Flax/epoxy, (c) Hemp/epoxy, (d) Ramie/epoxy, (e) Jute/epoxy, and (f) Kenaf/epoxy |
3.1 QUBO 공식화와 QA적용
QA 수행을 위해서는 해결하고자 하는 조합 최적화 문제가 정의되어야 하며, 이는 QUBO형태로 표현되어야 한다. QUBO 모델은 이진 변수 간의 상호작용을 에너지 항의 형태로 표현하며, 각 변수는 0 또는 1(Binary variable)의 값을 가지는 선택 상태를 나타낸다. QUBO의 목적은 이러한 이진 변수들의 조합에 대해 전체 에너지(목적함수 값)가 최소가 되도록 하는 구성을 찾는 것이다[28,29].
본 연구에서는 천연 하이브리드 복합재의 충격 흡수 에너지가 최대가 되며, 제시된 비중 및 비용 조건을 만족하는 적층 조합을 찾고자 한다. 곡률 반경, 비중 그리고 비용에 대한 값은 각 변수의 단위 차이에 따른 왜곡된 계수 영향도를 제거하기 위해 Max-min normalization을 통한 전처리가 선행되었다.
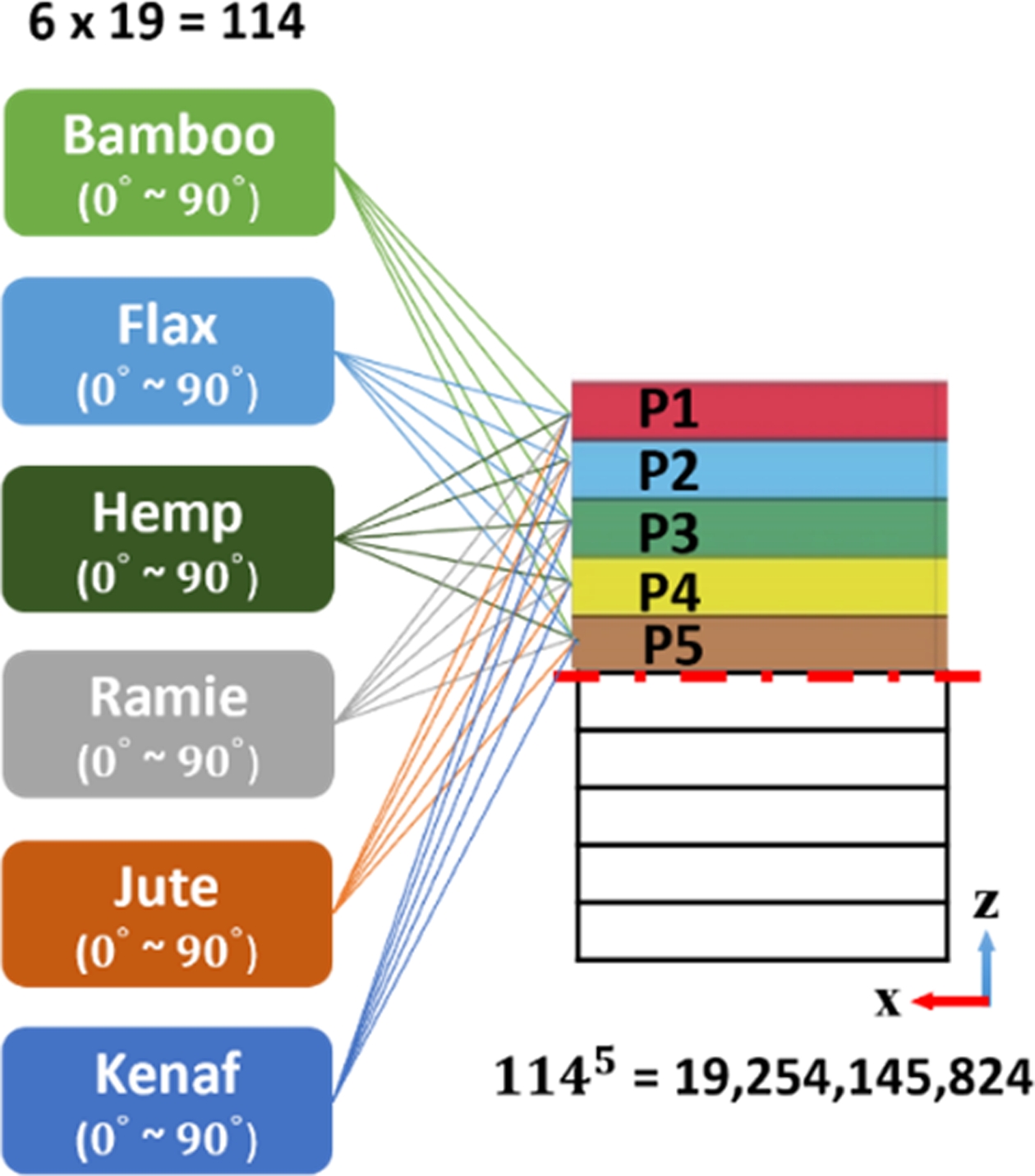
곡률 반경은 순수 굽힘 조건에서의 변형 저항성을 나타내는 지표로, 값이 작을수록 높은 휨 강성과 변형 저항성을 의미한다. 따라서 곡률 반경의 가중치 합을 최소화하는 것은 충격 하중 하에서의 에너지 흡수 능력을 최대화하는 물리적 목표와 동등하다[30,31]. 즉, 곡률 반경과 충격 흡수 에너지는 역비례 관계에 있으며, 샤르피 충격 초기 구간에서의 에너지 전달 및 손상 분산에 영향을 미치는 물성 지표로 활용될 수 있다. 이에 Fig. 2에서와 같이, 천연섬유의 종류와 섬유 배향 각도에 따른 굽힘 하중 특성을 나타내는 총 114개의 곡률 반경 데이터가 활용된다. 각 데이터는 P1에서 P5 플라이에 배치될지 여부를 나타내는 이진변수로 표현되며, 해당 변수에 대응하는 곡률 반경 값이 가중치로 곱해진다. 따라서 충격 흡수 에너지를 최대화하기 위한 목적함수는 섬유 종류 및 각도에 따라 배열된 114개의 곡률 반경 데이터에 대해 선택 유무를 나타내는 이진변수와 그에 대응하는 곡률 반경 가중치의 곱의 합이 최소가 되도록 정의될 수 있다. 이때, P1에서 P5 플라이에 적용될 수 있는 전체 가용 조합의 수는 Fig. 3에서와 같이 1145 = 19,254,145,824 가지에 해당한다.
제안된 목적함수는 다음 식 (2)과 같이 QUBO 형태로 표현될 수 있다.

여기서 i는 i∈{1,2,...,114}를 만족하는 굽힘 하중 특성을 나타낼 114개의 가중치 인덱스를 의미한다. Ri는 i번째 곡률반경 가중치에 해당하며, xi는 x∈{0,1}를 만족하는 이진변수를 나타낸다.
비중과 비용에 대한 제약조건은 다음 식 (3)-(4)와 같다.

여기서 ρi와 γi는 i번째 천연섬유 복합재의 비중과 섬유의 단위 중량당 비용을 의미하며, S와 C는 전체 천연 하이브리드 복합재의 비중과 단위 중량당 비용에 대한 제약을 의미한다. 비중 제약은 Table 3에 따른 최대 비중인 1.41(≅1.414)1.414)이 상한, 1.40, 1.38 그리고 비중이 가장 낮은 1.36(≅1.357)1.357)이 하한으로 설정되었으며, 해당 4가지 제약조건에 대해 각각 다르게 적용된다. 비용은 Table 1에서 천연섬유 후보의 평균인 1.1 $/kg이 제약조건으로 적용되었다.
각 플라이에서는 하나의 천연섬유만 선택되어야 하므로 이를 위한 제약 조건이 다음 식 (5)과 같이 추가로 정의되었다.

여기서 k는 k∈{1,2,3,4,5}를 만족하는 P1부터 P5에 대한 플라이 번호에 해당한다.
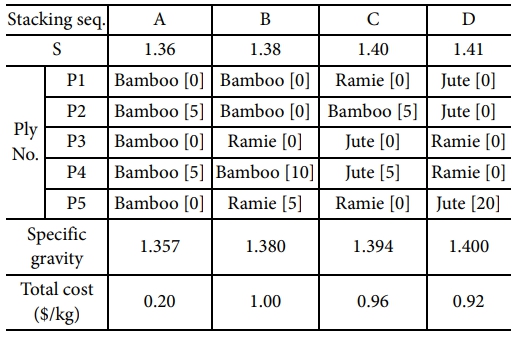
공식화된 식 (2)-(5)은 D-Wave에서 제공하는 파이썬 기반의 Ocean SDK(Software Development Kit)[32]를 통해 프로그래밍 되었으며, 양자 클라우드 서비스를 통해 상용 양자 어닐러에 임베딩되었다. QA는 4가지 경우에 대한 비중 제약조건(S)이 다르게 반영되어 총 4번 수행되었다. 전체 조합 최적화 평균 수행 시간은 5.057s, QPU(Quantum processing unit) 접속 시간은 평균 32 ms가 소요되었으며, 비중과 비용에 대한 제약조건을 만족하면서 충격 흡수 에너지가 최대가 되는 천연 하이브리드 복합재의 적층 순서 결과는 다음 Table 4와 같다.
3.2 충격 특성 평가를 위한 유한요소해석
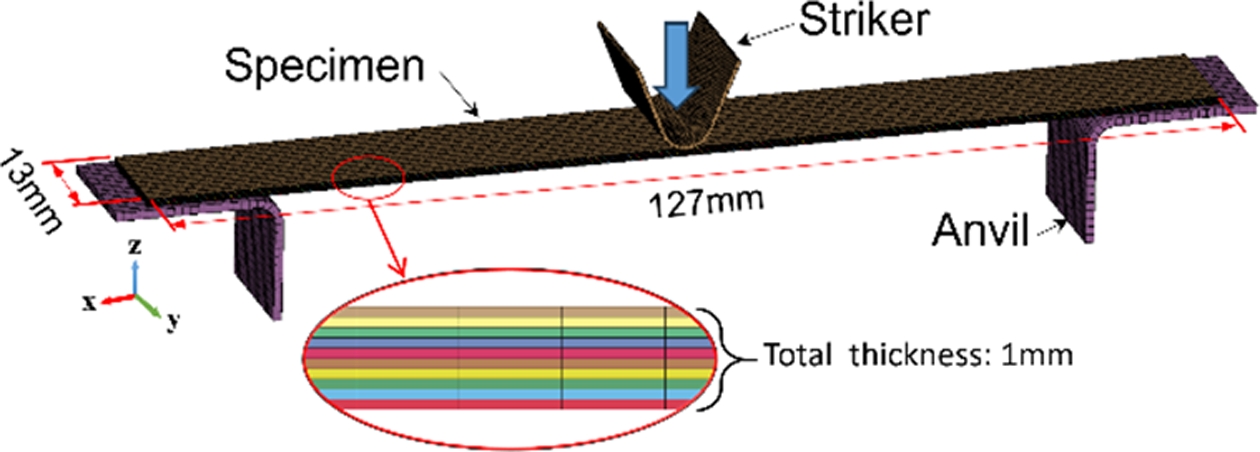
QA를 통해 도출된 천연 하이브리드 복합재의 적층 조합에 따른 충격 흡수 에너지를 평가하기 위해, ASTM D6110[33] 기준을 충족하는 샤르피 충격 시험이 Fig. 4와 같이 ANSYS/LS-DYNA를 활용한 유한요소 해석으로 구현되었다. 적용된 시편의 형상은 길이 127 mm, 너비 13 mm이며, 두께 0.1 mm의 플라이 10장이 적층되어 총 두께는 1 mm로 구성된다. 시편은 총 16,510개의 element로 구성되며, 요소 형상은 1 mm 크기의 hexahedral element가 적용되었다. 복합재의 기계적 거동을 구현하기 위해 MAT_054 Enhanced Composite Damage 모델이 적용되었으며, 섬유별 파단 연신율(Table 1)은 effective failure strain으로 입력되어 충격에 의한 파단 거동이 반영되었다. 각 플라이 간의 층간 접착 조건은 Automatic Surface-to-Surface Tiebreak 접촉 방식으로 정의되었으며, 15 kg의 하중을 갖는 스트라이커가 초기 속도 4 m/s로 시편에 충격을 가하는 조건으로 시뮬레이션이 수행되었다.
|
Fig. 3 Total available combinations |
|
Fig. 4 Charpy FEA model of natural hybrid composite |
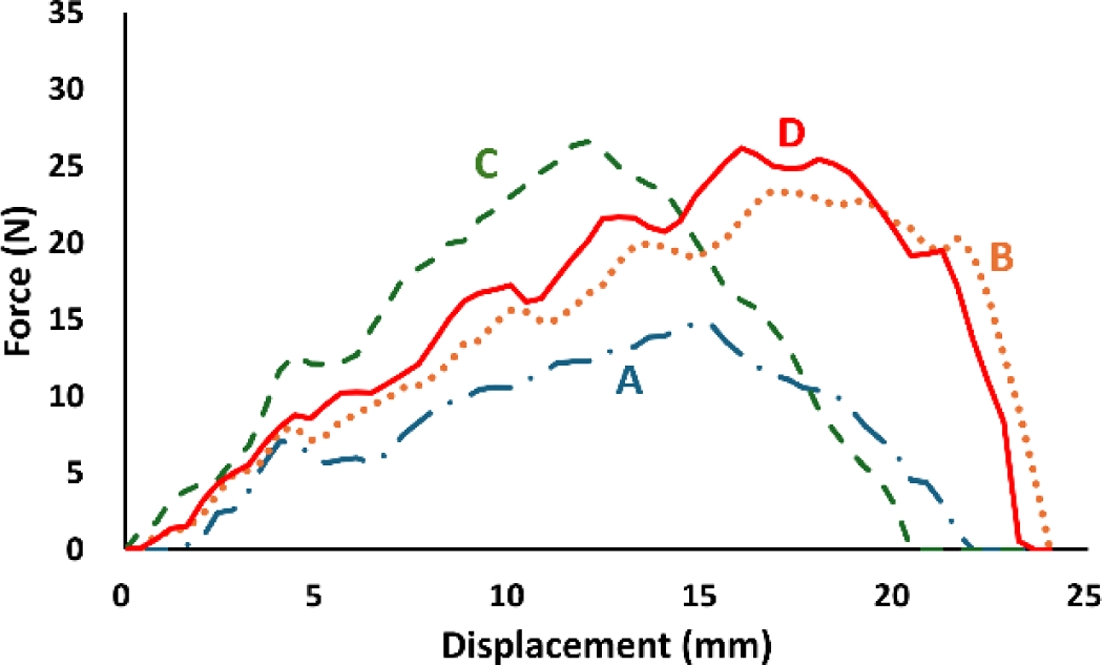
Table 4의 비중 제약조건에 따라 설정된 4가지 적층 조합(A, B, C, D)에 대한 샤르피 충격 해석 결과는 Fig. 5에 제시되어 있다. 전체 비중이 가장 낮은 조합 A에서는 최대 피크 하중이 14.8 N으로 가장 낮게 나타난 반면, 조합 C에서는 26.6 N으로 가장 높은 값을 기록하였다. 이러한 차이는 각 조합의 적층 구조 내에서 고강성 섬유의 배치 위치에 기인한 것으로 판단된다. 특히 조합 C에서는 충격 하중에 가장 민감하게 반응하는 외곽층(P1)에 E1이 74.97 GPa로 가장 높은 Ramie 섬유가 배치되어 있어, 초기 충격에 대한 저항력이 크게 향상된 것으로 해석된다.
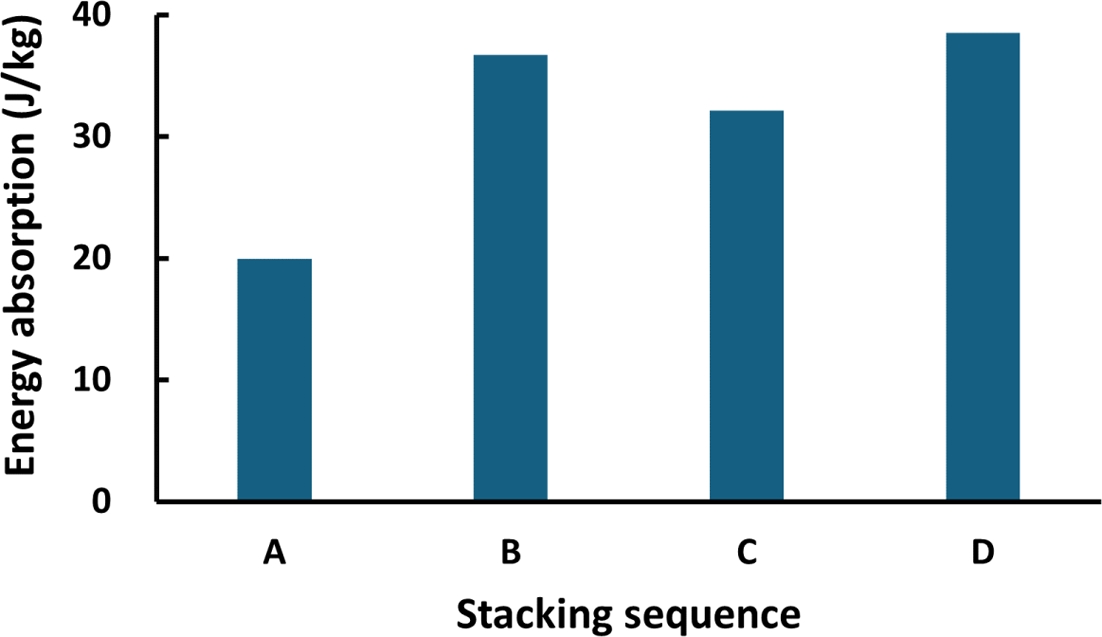
Fig. 6에 제시된 바와 같이, 충격 흡수 에너지는 조합 A에서 19.95 J/kg, 조합 B에서는 27.42 J/kg, 조합 C에서는 35.08 J/kg으로 도출되었으며, 조합 D에서 38.56 J/kg으로 가장 높게 나타났다. 조합 A는 Bamboo 섬유 중심의 적층으로 구성되어 있으며, 낮은 탄성계수(35 GPa), 인장강도(0.5 GPa), 짧은 파단 연신율(1.4%)로 인해 충격 하중에 대한 저항력이 제한적이었다. 이에 따라 충격 하중 분산이 충분히 이루어지지 않아 충격 흡수 에너지가 가장 낮게 도출된 것으로 분석된다.
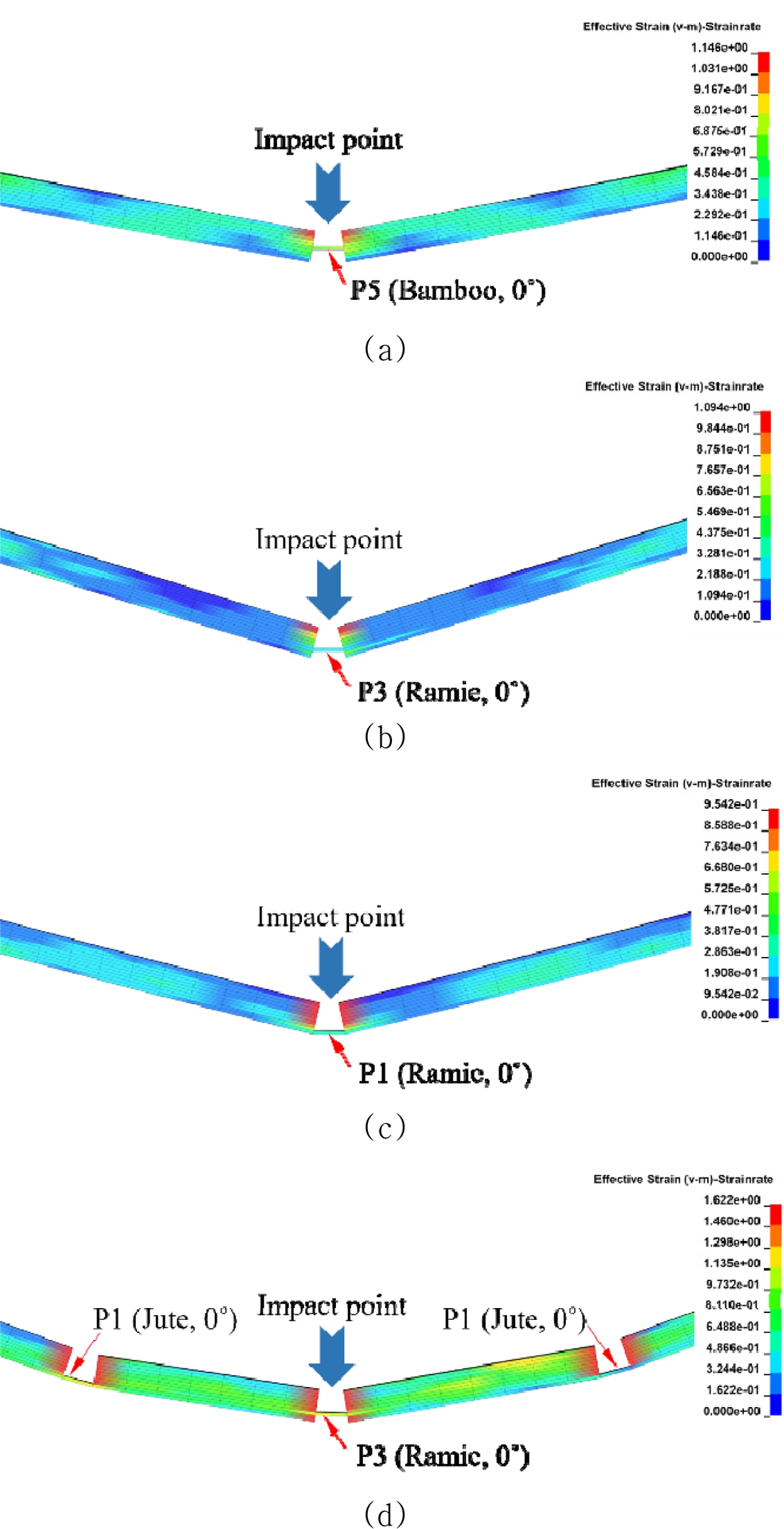
Fig. 7은 충격 하중에 의한 조합 A, B, C, D에 대한 천연 하이브리드 복합재의 파단 거동을 나타내며, 조합 A, B, C의 경우 충격 지점에서만 파단이 발생된 것을 Fig. 7(a)-(c)를 통해 알 수 있다. 반면 조합 D에 대한 결과인 Fig. 7(d)에서는 파단이 단일 지점에 집중되지 않고, 복수 지점에 걸쳐 분산되어 발생함으로써 국부 응력 집중을 완화하고 총 소산 에너지가 증가하는 구조 거동을 보였다.
조합 D는 Jute와 Ramie 섬유가 혼합된 구조로, Jute는 E1이 24.81 GPa, 연신율이 1.8%이며, Ramie는 가장 높은 E1(74.97 GPa)과 Jute 대비 상대적으로 높은 연신율(3.8%)을 나타낸다. 특히 외곽층(P1, P2)에 0°로 배치된 Jute는 낮은 연신율로 인해 초기 충격 하중에 국부적인 파괴가 발생할 가능성이 있으나, 중간층(P3, P4)에 동일하게 0°로 배치된 Ramie가 높은 강성과 연성을 바탕으로 구조적 하중을 효과적으로 지지하고, 에너지를 효율적으로 흡수한 것으로 해석된다. 또한 최내층(P5)에 20°로 배치된 Jute는 사선 방향의 섬유 배향을 통해 응력 전달을 분산시키고, 균열이나 파단이 특정 방향으로 집중되는 현상을 억제하는 데 기여한 것으로 판단된다. 이러한 섬유 배열은 파단 경로를 다중으로 분산시켜 손상 확산을 지연시키는 효과를 유도한다. 이와 같이 각 플라이의 상호보완적 충격 거동 특성이 조합 D의 전체 구조적 저항성을 향상시켰으며, 결과적으로 네 가지 조합 중 가장 높은 충격 흡수 에너지를 기록한 주요 요인으로 평가된다.
한편, Kenaf 섬유는 Table 3에서 나타난 바와 같이 E1(4.46 GPa)과 E2(4.39 GPa)가 거의 동일하여 등방성에 가까운 거동을 보였다. 이러한 특성으로 인해 섬유 배향 각도 변화에 따른 곡률 반경의 민감도가 매우 낮았으며, 굽힘 하중에 대한 저항성 기여가 제한적이었다. 따라서 QUBO 기반 최적화 과정에서 Kenaf의 가중치가 낮게 반영되어, Table 4에서 최종 QA 결과의 4가지 최적 조합(A–D)에는 포함되지 않은 것으로 판단된다.
|
Fig. 5 FD curve results according to stacking sequence |
|
Fig. 6 Energy absorption results according to stacking sequence |
|
Fig. 7 Impact behavior results according to stacking sequence: (a) A, (b) B, (c) C, and (d) D |
본 연구에서는 천연 하이브리드 복합재의 충격 흡수 성능 향상을 목적으로, 적층 순서를 양자 어닐링(Quantum Annealing, QA)을 통해 최적화하고 그 구조 응답을 유한요소해석 기반의 샤르피 충격 시뮬레이션으로 평가하였다. 총 6종의 천연섬유와 19가지 섬유 배향 조합으로 구성된 114개의 곡률 반경 데이터를 기반으로 목적함수를 정의하고, QUBO 형태로 변환하여 QA에 임베딩하였다. 비중 과 비용 제약 조건을 만족하는 4가지 조합(A~D)을 도출하였으며, 각 조합에 대한 충격 흡수 에너지는 해석 결과 A: 19.95 J/kg, B: 27.42 J/kg, C: 35.08 J/kg, D: 38.56 J/kg로 나타났다. 특히, 조합 D는 Ramie와 Jute의 강성과 연성이 상호 보완되는 구조로 적층 조합이 도출되었다. 외곽층(P1, P2)의 0°로 배향된 Jute는 초기 충격을 흡수하고, 중간층(P3, P4)의 0°로 배향된 Ramie는 높은 하중을 지지하며, 최내층(P5)의 20°로 배향된 Jute는 응력 분산을 유도하여 파단 경로의 다중화를 가능하게 하였다. 이러한 적층 구조는 충격 지점 외에도 두 개의 보조 파단 지점을 발생시켜 손상 분산과 에너지 소산이 극대화되었으며, 그 결과 가장 높은 충격 흡수 에너지(38.56 J/kg)를 나타낼 수 있었다.
본 연구는 적층 순서, 섬유 종류, 배향이 복합재의 동적 거동에 미치는 영향을 정량적으로 분석하였으며, 친환경 복합재의 설계 문제에 양자 기반 조합 최적화 기법을 실질적으로 적용할 수 있음을 제시하였다.
향후 다양한 하중 조건 및 제조 공정 변수와 연계된 최적 설계 확장에도 본 연구의 접근 방식이 유효하게 적용될 수 있을 것으로 기대된다.
이 연구는 2025년도 산업통상자원부 및 한국산업기술기획평가원(KEIT) 연구비 지원에 의한 연구임 (‘20017947’) 또한 이 논문은 2023년도 정부(과학기술정보통신부)의 재원으로 한국연구재단 양자정보과학 연구개발생태계 조성사업의 지원을 받아 수행된 연구임(2020M3H3A1110365).
- 1. Ahmad, F., Choi, H.S., and Park, M.K., “A review: Natural fiber composites selection in view of mechanical, light weight, and economic properties,” Macromolecular Materials and Engineering, Vol. 300, No. 1, 2015, pp. 10–24.
-

- 2. Oh, E., Zuniga, M.M.G., and Suhr, J., “Trends and Perspective for Eco-friendly Composites for Next-generation Automobiles,” Composites Research, Vol. 37, No. 2, 2024, pp. 115–125.
-

- 3. Lee, D.W., Li, M., and Song, J.I., “Study on the Improvement of Flame Retardancy of Bamboo Fiber Using Eco-Friendly Liquid Flame Retardant,” Composites Research, Vol. 35, No. 6, 2022, pp. 456–462.
- 4. Venkatarajan, S., and Athijayamani, A., “An overview on natural cellulose fiber reinforced polymer composites,” Mater Today Proc., Vol. 37, No. 2, 2020, pp. 3620–3624.
-

- 5. Nurihan, O., Hisham, M.R.M., Rasid, Z.A., and Hassan, M.Z., “The elastic properties of unidirectional bamboo fibre reinforced epoxy composites,” Journal of Recent Technology and Engineering, Vol. 8, No. 3, 2019, pp. 7187–7193.
-

- 6. Shin, H., Lee, J., Moon, S., and Lee, J., :Structural Test Analysis Study for Manufacturing of Flax Fiber Composite Blades for 30kW Wind Turbines,” Composites Research, Vol. 36, No. 1, 2023, pp. 32–36.
-

- 7. Azim, A.Y.M.A., Alimuzzaman, S., and Sarker, F., “Optimizing the Fabric Architecture and Effect of I-Radiation on the Mechanical Properties of Jute Fiber Reinforced Polyester Composites,” ACS Omega, Vol. 7, No. 12, 2022, pp. 10127–10136.
-

- 8. Gnaba, I., Wang, P., Soulat, D., Omrani, F., Ferreira, M., and Vroman, P., “Investigation about the effect of manufacturing parameters on the mechanical behaviour of natural fibre nonwovens reinforced thermoplastic composites,” Materials (Basel), Vol. 12, No. 16, 2019, 2560.
-

- 9. Ghani, U.M., Siddique, A., Abraha, G.K., Yao, L., Li, W., Khan, M.Q., and Kim, I.S., “Performance Evaluation of Jute/Glass-Fiber-Reinforced Different Layering Configurations,” Materials (Basel), Vol. 15, No. 3–4, 2022, 1055.
-

- 10. Oliveira, M., Neves, V., and Banea, M.D., “Mechanical and Thermal Characterization of Bamboo and Interlaminar Hybrid Bamboo/Synthetic Fibre-Reinforced Epoxy Composites,” Materials (Basel), Vol. 17, No. 8, 2024, 1777.
-

- 11. Yang, K., Wu, S., Guan, J., Shao, Z., and Ritchie, R.O., “Enhancing the Mechanical Toughness of Epoxy-Resin Composites Using Natural Silk Reinforcements,” Scientific Reports, Vol. 7, No. 1, 2017, 11939.
-

- 12. Singh, Y., Singh, J., Sharma, S., Lam, T.D., and Nguyen, D.N., “Fabrication and characterization of coir/carbon-fiber reinforced epoxy based hybrid composite for helmet shells and sports-good applications: influence of fiber surface modifications on the mechanical, thermal and morphological properties,” Journal of Materials Research and Technology, Vol. 9, No. 6, 2020, pp. 15593–15603.
-

- 13. Zhao, R.-X., Qahan: A Quantum Annealing Hard Attention Network, 2024.
-

- 14. Adachi, S.H., and Henderson, M.P., “Application of Quantum Annealing to Training of Deep Neural Networks,” Proc Sci. 2015, 30-July-20(Cd):1–18.
-

- 15. Boyda, E., Basu, S., Ganguly, S., Michaelis, A., Mukhopadhyay, S., and Nemani, R.R., “Deploying a quantum annealing processor to detect tree cover in aerial imagery of California,” PLoS One, Vol. 12, No. 2, 2017, pp. 1–22.
-

- 16. López-Alba, E., Schmeer, S., and Díaz, F., “Energy absorption capacity in natural fiber reinforcement composites structures,” Materials (Basel), Vol. 11, No. 3, 2018, 418.
-

- 17. Saleem, A., Medina, L., Skrifvars, M., and Berglin, L., “Hybrid Polymer Composites of Bio-Based Bast Fibers with Glass, Carbon and Basalt Fibers for Automotive Applications—A Review,” Molecules, Vol. 25, No. 21, 2020.
-

- 18. Prabhudass, J.M., Palanikumar, K., Natarajan E., and Markandan, K., Enhanced Thermal Stability, Mechanical Properties and Structural Integrity of MWCNT Filled Bamboo/Kenaf Hybrid Polymer Nanocomposites,” Materials (Basel), Vol. 15, No. 2, 2022, 506.
-

- 19. Wang, X., Wang, L., Ji, W., Hao, Q., Zhang, G., and Meng, Q., “Characterization of KH-560-modified jute fabric/epoxy laminated composites: Surface structure, and thermal and mechanical properties,” Polymers (Basel), Vol. 11, No. 5, 2019, 769.
-

- 20. Alajmi, A.E., Alotaibi, J.G., Yousif, B.F., andd Nirmal, U., “Tribological studies of bamboo fibre reinforced epoxy composites using a bod technique,” Polymers (Basel), Vol. 13, No. 15, 2021, 2444.
-

- 21. Gargol, M., Klepka, T., Klapiszewski Ł., and Podkościelna, B., “Synthesis and thermo-mechanical study of epoxy resin-based composites with waste fibers of hemp as an eco-friendly filler,” Polymers (Basel), Vol. 13, No. 4, 2021, 503.
-

- 22. Dal Pont, B., Gigante, V., Panariello, L., Canesi, I., Aliotta, L., and Lazzeri, A., “Investigation of Novel Flax Fiber/Epoxy Composites with Increased Biobased Content,” Polymers (Basel), Vol. 15, No. 19, 2023, 4030.
-

- 23. Thomason, J.L., “Why are natural fibres failing to deliver on composite performance?,” 17th Int Conf Compos Mater. 2009.
- 24. Mariselvam, V., and Logesh, M., “Analytical analysis on material properties of Kenaf fiber composite,” International Journal of Applied Engineering Research, Vol. 10, No. 50, 2015, 617–620.
- 25. Hexcel Composites. Product data HexPly 8552. Hexcel. 2000, Vol. 1, No. 1, 1–6.
- 26. Anastasiou, D.E., “The exponential model versus a modified Chamis model and applications to sustainable particulate composites,” Journal of Applied Polymer Science, Vol. 140, No. 27, 2023, e54014.
-

- 27. Marshall, I.H., “Axiomatic Design and Fabrication of Composite Structures: Applications in Robots, Machine Tools, and Automobiles (Oxford Series on Advanced Manufacturing),” Ind. Robot An Int. J., Vol. 33, No. 2, 2006.
-

- 28. Hauke, P., Katzgraber, H.G., Lechner, W., Nishimori, H., and Oliver, W.D., “Perspectives of quantum annealing: Methods and implementations,” Reports on Progress in Physics, Vol. 83, 2020, 054401.
-

- 29. Albash, T., and Lidar, D.A., “Adiabatic quantum computation,” Reviews of Modern Physics, 2018, Vol. 90, No. 1, 15002.
- 30. Seifoori, S., Parrany, A.M., and Mirzarahmani, S., “Impact damage detection in CFRP and GFRP curved composite laminates subjected to low-velocity impacts,” Composite Structures, 2021, Vol. 261, 2020, 113278.
-

- 31. Zhu, X., Xiong, C., Yin, J., Zhou, H., Deng, H., and Zou, Y., “Bending responses of CFRP thin-walled tubes with different sectional shapes : Experimental, analytical and numerical investigation,” Composite Structures, Vol. 304, No. 1, 2023, 116374.
-

- 32. D-Wave Ocean Documentation, https://docs.dwavequantum. com/en/latest/index.html, 2025.
- 33. Astm-D6110-10. Standard Test Method for Determining the Charpy Impact Resistance of Notched Specimens of Plastics. Astm. 2010, 17.
-

 This Article
This Article
-
2025; 38(6): 649-656
Published on Dec 31, 2025
- 10.7234/composres.2025.38.6.649
- Received on Aug 6, 2025
- Revised on Oct 7, 2025
- Accepted on Nov 11, 2025
 Services
Services
- Abstract
1. 서 론
2. 천연섬유 복합재의 플라이별 곡률 반경 분석
3. qa를 통한 최적해 도출과 충격특성 평가
4. 결 과
5. 결 론
- 후기
- References
- Full Text PDF
Shared
 Correspondence to
Correspondence to
- Seong S. Cheon
-
Department of Mechanical Engineering, Graduated School, Kongju National University
- E-mail: sscheon@kongju.ac.kr






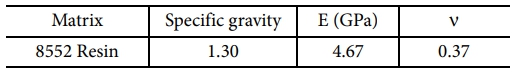
 Copyright ⓒ The Korean Society for Composite Materials. All rights reserved.
Copyright ⓒ The Korean Society for Composite Materials. All rights reserved.