In this study, the material behavior of molded pulp, an environmentally friendly packaging material, was experimentally characterized and numerically analyzed using the finite element method. To this end, quasi-static and high strain-rate tensile tests, as well as quasi-static in-plane compression tests, were conducted. Based on the experimental results, finite element analyses were performed using the MAT_PLASTICITY_COMPRESSION_TENSION material model in LS-DYNA. For the in-plane compression tests, a comb-type fixture was designed and fabricated to suppress global buckling, enabling effective measurement of the in-plane compressive behavior. The molded pulp material exhibited significantly different mechanical responses under tension and compression, and substantial discrepancies were also observed between through-thickness compression and in-plane compression behaviors. In addition, pronounced strain-rate effects were identified under both tensile and compressive loading conditions. These material characteristics of molded pulp were effectively captured using the MAT_PLASTICITY_COMPRESSION_ TENSION model. Furthermore, the numerical simulations showed good agreement with experimental impact test results of molded pulp products.

본 논문에서는 친환경 포장재인 펄프몰드의 재료 거동을 측정하고 이를 기반으로 유한요소해석을 수행하였다. 이를 위해 저속 및 고속 인장 시험과 저속 압축 시험을 실시하였으며, 실험 결과를 바탕으로 LS-DYNA의 MAT_PLASTICITY_COMPRESSION_TENSION 모델을 적용하여 유한요소해석을 수행하였다. 면내 압축 시험에서는 좌굴을 억제하기 위하여 빗살 형태의 지그를 설계·제작하였으며, 이를 통해 면내 압축 거동을 효과적으로 측정할 수 있었다. 펄프몰드 소재는 인장과 압축 거동이 현저히 상이하였으며, 두께 방향 압축 거동과 면내 압축 거동 간에도 큰 차이가 나타났다. 또한 인장, 압축 조건 모두에서 변형률 속도 효과가 뚜렷하게 관찰되었다. 이러한 펄프몰드 소재의 재료 거동 특성은 MAT_PLASTICITY_COMPRESSION_TENSION 모델을 통해 효과적으로 고려될 수 있었으며, 펄프몰드 제품에 대한 충격 시험 결과와 유한요소해석 결과가 전반적으로 잘 일치하였다.

Keywords: 펄프몰드(Molded pulp), 충격해석(Impact analysis), 재료시험(Material test), 좌굴억제(Anti-buckling)

발포 폴리스티렌(EPS, Expanded Polystyrene)은 우수한 단열 특성과 완충 특성으로 인해 포장재 소재로 많이 사용되지만, 생분해가 거의 불가능하여 환경적 문제를 유발하게 된다. 이와 같은 포장재의 환경적 문제를 해결하기 위해 친환경 소재인 펄프몰드(Molded Pulp)의 사용이 점차 증가하고 있다. 펄프몰드는 종이 성형품으로 고지 소재를 활용하여 성형되기 때문에 재활용 및 생분해가 가능한 친환경 소재이며, 가볍고 충격과 진동을 잘 흡수하는 성질이 있으므로 포장용 완충재로 사용되고 있다. 다만 EPS와 달리 두께가 얇기 때문에 두께 방향 압축에 의한 완충 효과는 상대적으로 적다. 펄프몰드는 구조 변형, 국부 응력 집중, 최초 국부 좌굴, 응력 재분배, 전체 좌굴, 구조 붕괴 및 치밀화(densification)에 이르는 변형 과정을 통해 순차적 변형으로 충격에너지를 흡수하게 된다.
펄프몰드의 완충 성능 분석을 위하여 Park[1]은 응력–에너지 방법론을 적용하여 완충 곡선(Cushion Curve) 모델을 도출하였으며, 제품의 완충 성능은 재료 특성보다 구조적 인자에 의해 더 크게 영향을 받는 것을 언급하였다.
펄프몰드를 이용하여 최적의 완충효과를 갖는 포장제품 설계를 위해 유한요소해석이 활용되고 있으며, 이 경우 해당 소재의 거동을 잘 모사하기 위한 구성방정식이 중요하다. 그러나 섬유질 기반의 다공성 소재인 펄프몰드는 제조과정에서 섬유의 배향과 건조시 발생하는 구속력으로 인해 이방성을 갖는 적층 구조를 형성하는 것으로 알려져 있으나, 구성방정식에 대한 연구는 거의 진행되지 않은 상태이다. Li[2]는 이와 같은 적층 구조로 인하여 면내에서의 강성과 두께 방향으로의 강성은 큰 차이를 갖고 있음을 보였으며, 섬유의 분포나 연결 구조가 소재의 특성에 미치는 영향을 분석하고자 하였다.
Gurav[3]는 펄프몰드의 압축 거동은 충격에너지 흡수를 분석하기 위한 핵심적인 물성이며, 인장 거동과 비교할 때 일반적으로 강도가 더 낮게 나타남을 확인하였다. 따라서 펄프몰드의 재료거동을 파악하기 위해서는 인장거동과 압축거동이 모두 측정될 필요가 있으며, 압축 거동은 두께 방향 보다는 면내(In-Plane) 방향의 압축 거동이 중요함을 알 수 있다. 따라서 얇은 판재형 소재의 좌굴을 방지할 수 있는 압축실험이 중요하다.
Dislaire[4]는 서로 다른 6종의 목재 섬유를 사용한 펄프몰드 소재의 인장 특성에 대한 비교를 수행하였으며, 사용된 섬유의 종류에 따라 유의미한 차이가 나타남을 확인하였다. 펄프몰드의 특성에 영향을 주는 다양한 변수들 중 수분은 중요한 인자이며, 제조 공정과 사용단계에 있어 강한 영향을 미친다. Babbepalli[5]는 탄성 계수 및 경화 계수와 같은 기계적 물성을 수분 비율의 함수로 고려하고자 하였다.
Kowalewski[6]는 얇은 금속재료의 압축시험을 위해 시편 게이지 길이의 약 40%를 좌굴을 억제하여 압축할 수 있는 지그를 제안하였으며 좌굴을 효과적으로 방지할 수 있음을 보였다. Babaei[7]는 CFRP의 압축 시험을 위해 원통형 좌굴 방지 기둥을 사용하였으며 다양한 형상의 시편에 적용 가능함을 언급하였다. 펄프몰드 소재의 면내 압축을 위해 적용된 좌굴억제 지그에 대한 연구사례는 없으나, 펄프몰드 소재는 금속재료나 CFRP에 비하여 낮은 강도를 갖기 때문에 좌굴 억제를 위해 두께 방향으로 누르는 힘을 최소화해야 한다.
골판지나 골판지의 원재료인 원심지는 변형률 속도 효과가 있음을 보였으며[8], 펄프몰드 소재도 종이 재질의 소재이기 때문에 변형률 속도 효과가 있을 것으로 예상된다. Wang[9]은 변형률 속도가 증가함에 따라 몰드 펄프 제품의 항복강도가 뚜렷하게 증가함을 보였으며, 변형률 속도는 펄프몰드 제품의 하중 지지 능력과 에너지 흡수 특성에 큰 영향을 미치는 중요 인자인 것을 보였다. 다만 인장하중에 대해서는 변형률 속도를 고려하는 것이 가능하지만, 고속 면내 압축에 대해서는 좌굴을 억제해야 하기 때문에 실험적으로 구현이 어려울 것으로 보인다.
펄프몰드 소재는 친환경 소재이기 때문에 산업적으로 점차 활용이 증가하고 있으나 재료 거동에 대한 체계적인 연구들은 아직 활발히 진행되고 있지 않으며, 펄프몰드의 거동을 나타낼 수 있는 정립된 구성방정식은 없는 것으로 보인다. 종이 기반의 소재인 펄프몰드는 이방성 및 탄소성 거동을 보이며, 특히 면내 거동과 두께 방향 거동이 크게 다르다. 또한, 인장과 압축에서 재료 강도 차이가 크고 수분 함유량, 변형률 속도에 대한 민감도가 높다.
본 연구에서는 펄프몰드 제품의 충격 시험과 유한요소해석을 통해 실험–해석 간 상관성을 분석하고자 한다. 이를 위해 펄프몰드 제품에 대한 충격 실험을 수행하고, 그 결과를 유한요소해석 결과와 비교·분석하였다. 유한요소해석에는 LS-DYNA의 등방성 탄소성 물성 모델 중 하나인 MAT_PLASTICITY_COMPRESSION_TENSION 모델을 적용하여 인장과 압축 거동의 차이 및 변형률 속도 효과를 고려하였다. 본 물성 모델에 필요한 입력 데이터는 실험을 통해 확보하였다. 특히 펄프몰드의 면내 압축 거동을 정확히 평가하기 위해 좌굴을 억제할 수 있는 지그를 설계·제작하여 시험에 적용하였으며, 변형률 속도 효과를 고려하기 위해 고속 인장 시험을 수행하였다.

2.1 저속 및 고속 인장 시험
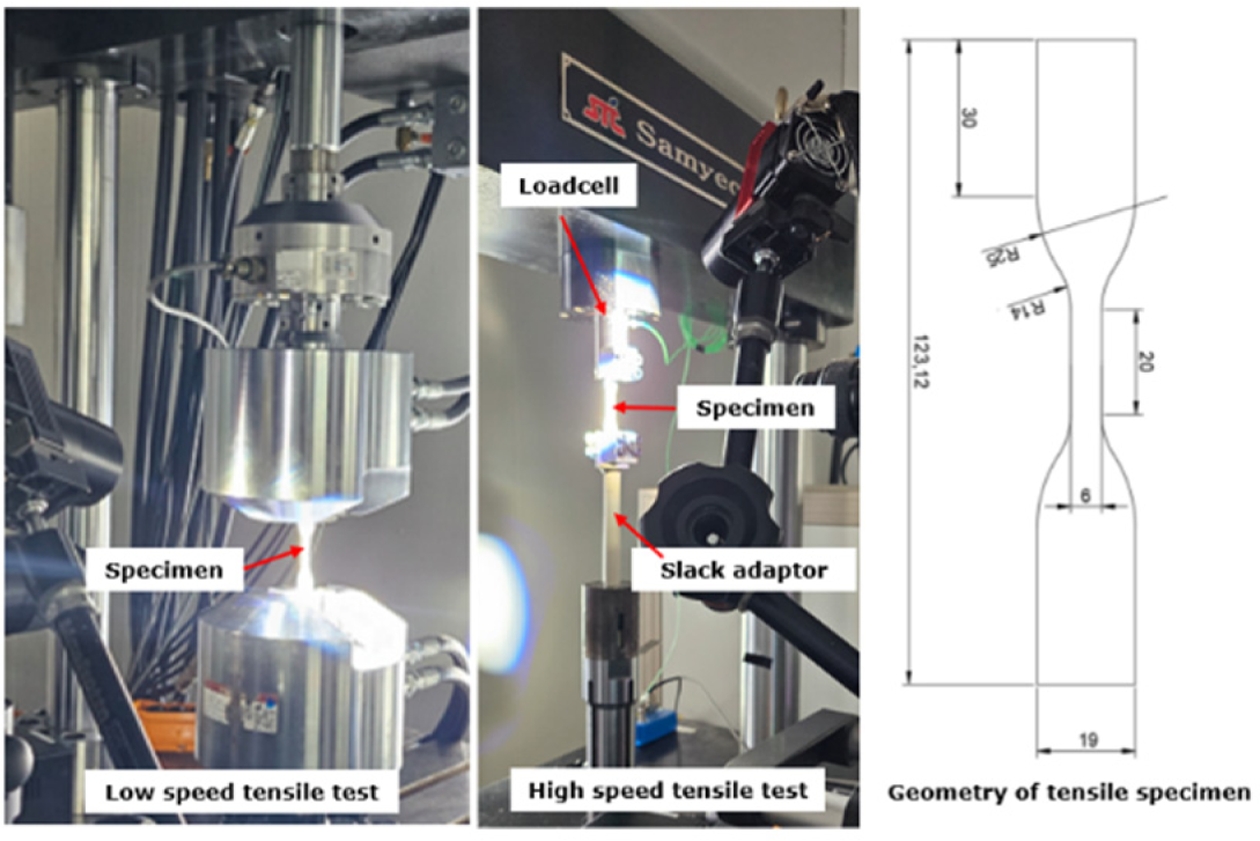
펄프몰드 소재의 물성 측정을 위해 저속 및 고속 인장 시험을 수행하였다. 시험은 변형률 속도 0.01/s, 0.1/s, 1/s, 10/s 및 100/s 조건에서 실시하였으며, ASTM D638 Type-IV 규격의 시편을 사용하였다. 사용된 시험기와 시편의 형상은 Fig. 1에 나타내었다. 시편의 변형률 계측을 위해 디지털 영상 상관법(Digital Image Correlation, DIC)을 적용하였다.
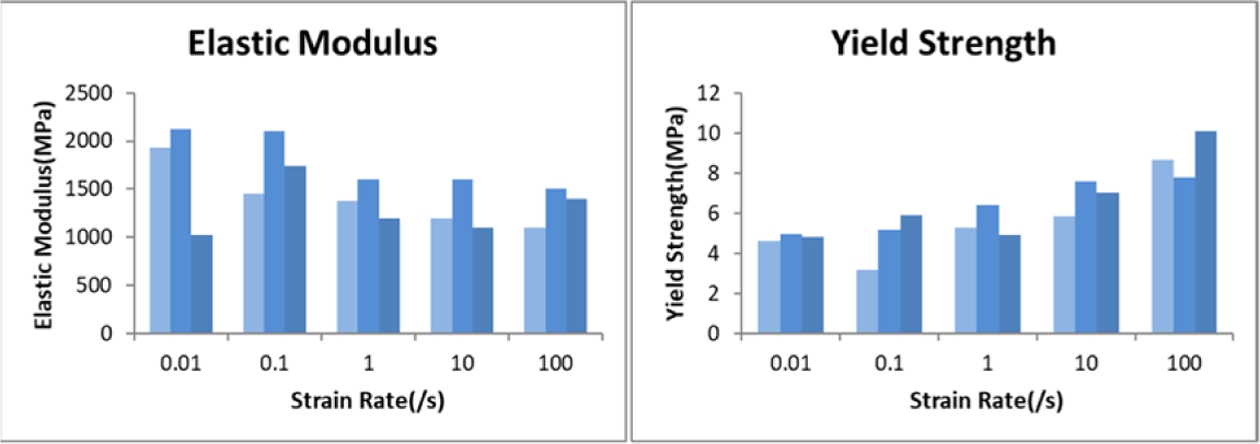
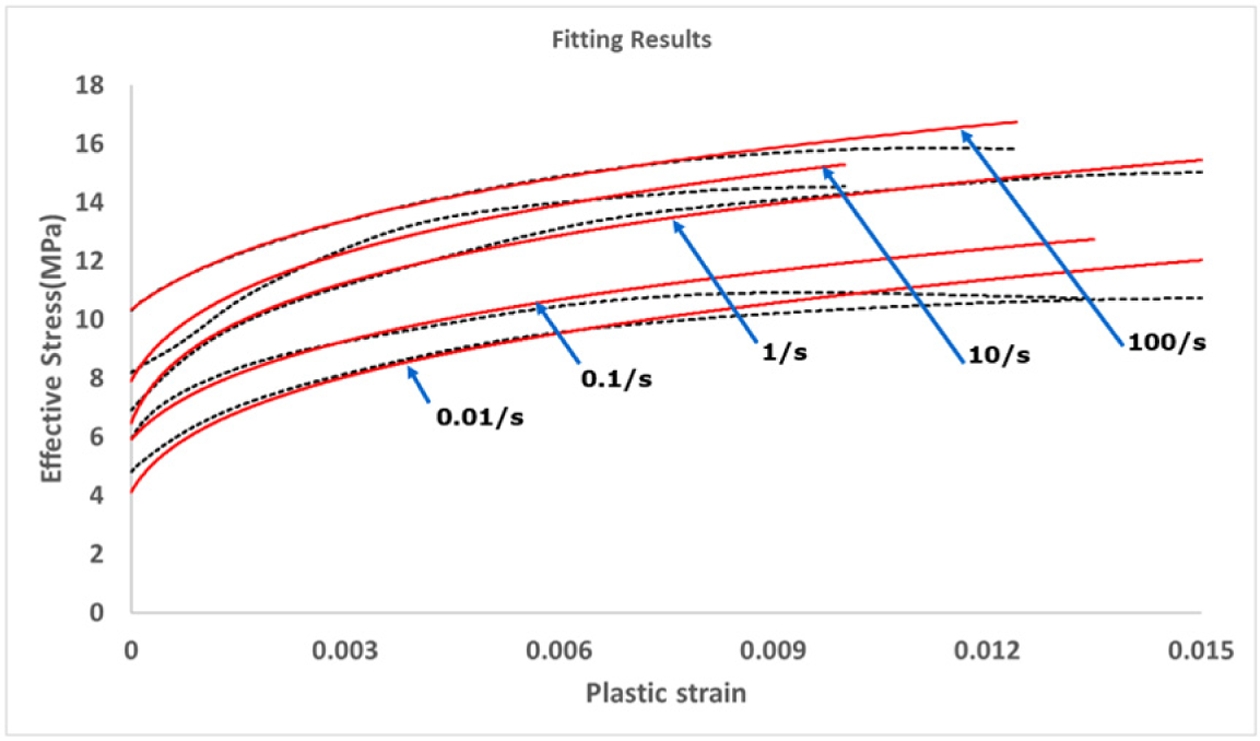
Fig. 2는 인장 시험 결과로부터 도출된 펄프몰드 소재의 탄성계수와 항복 강도를 나타낸 것이다. 탄성계수는 약 1,500 MPa 수준으로 나타났으며, 항복 강도는 변형률 속도가 증가함에 따라 증가하는 경향을 보였다. Fig. 3은 유한요소해석에 적용하기 위해 변형률 속도별 유효응력–소성 변형률 선도를 나타낸 것으로, 실험 결과와 Swift 경화식을 이용한 곡선 피팅 결과를 함께 제시하였다. 변형률 속도 증가에 따른 소재 강도의 상승이 명확히 관찰되었다.
2.2 저속 압축 시험
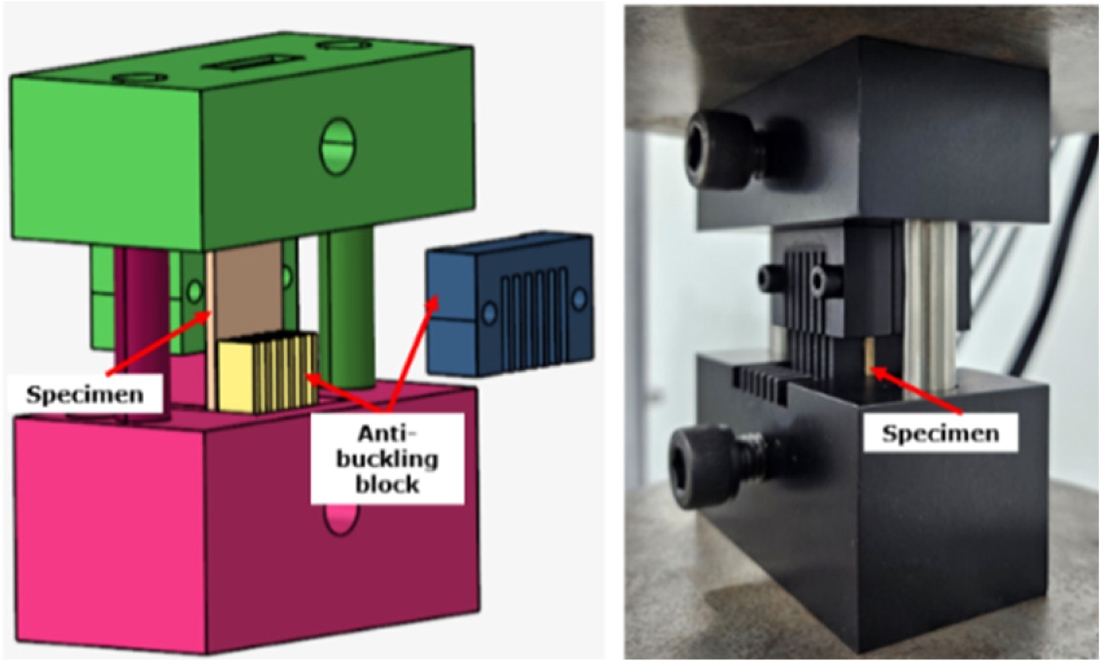
펄프몰드 소재의 압축 거동은 인장 거동과 차이를 보이며, 특히 두께 방향 압축보다 면내 압축 거동이 펄프몰드의 완충 특성에 더 큰 영향을 미친다. 이에 본 연구에서는 면내 압축 거동을 평가하기 위해 면내 압축 시험을 수행하였다. 면내 압축 시험의 경우 시편 두께가 2.0 mm로 얇아 좌굴 억제가 중요하므로, Fig. 4에 나타낸 바와 같이 빗살 형태의 두께 방향 블록을 적용하여 좌굴을 억제하였다. 압축 시편은 두께 2.0 mm의 직사각형 형상(20 mm × 90 mm)으로 제작하였으며, 게이지 길이는 10 mm로 설정하여 좌굴이 억제된 상태에서 약 10 mm의 압축 변형이 가능하도록 설계하였다.
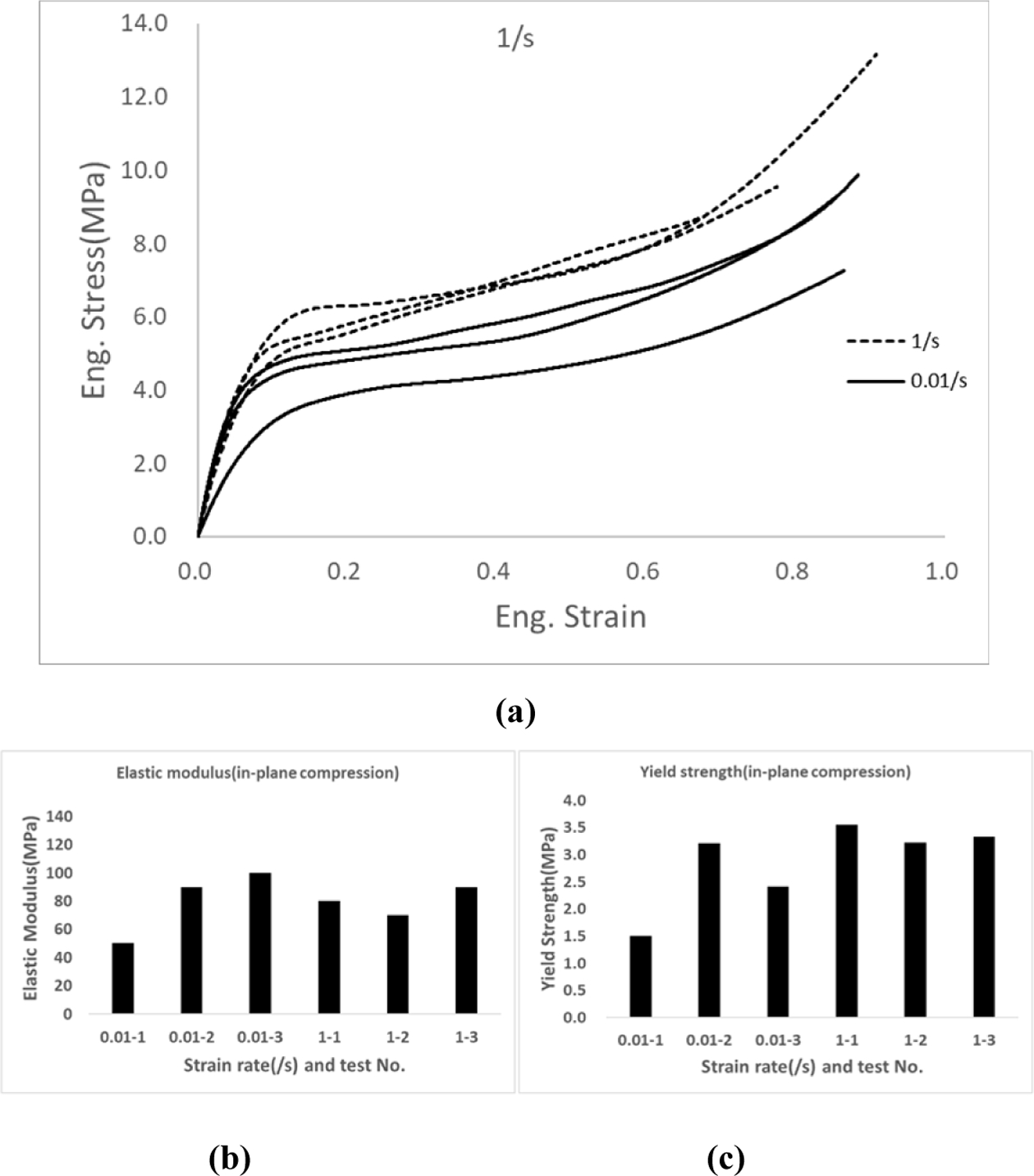
면내 압축 시험은 고속 인장 시험과 달리 0.01/s–100/s 범위의 변형률 속도에서 수행하기가 실험적으로 제한적이므로, 본 연구에서는 0.01/s와 1/s의 변형률 속도 조건에서 시험을 실시하였다. 측정되지 않은 변형률 속도 구간의 거동은 인장 시험 결과를 기준으로 내삽 또는 외삽하여 추정하였다. Fig. 5는 면내 압축 시험 중 시편의 변형 형상을 나타낸 것으로, 시험 과정에서 좌굴이 효과적으로 억제되었음을 확인할 수 있다. Fig. 6은 면내 압축 시험으로부터 얻어진 응력–변형률 선도와 탄성계수 및 항복 강도를 나타낸 것이다. 인장 시험에서의 탄성계수가 약 1,500 MPa인 반면, 면내 압축의 경우 약 90 MPa로 나타나 인장 탄성계수의 10% 이하 수준임을 확인하였다.
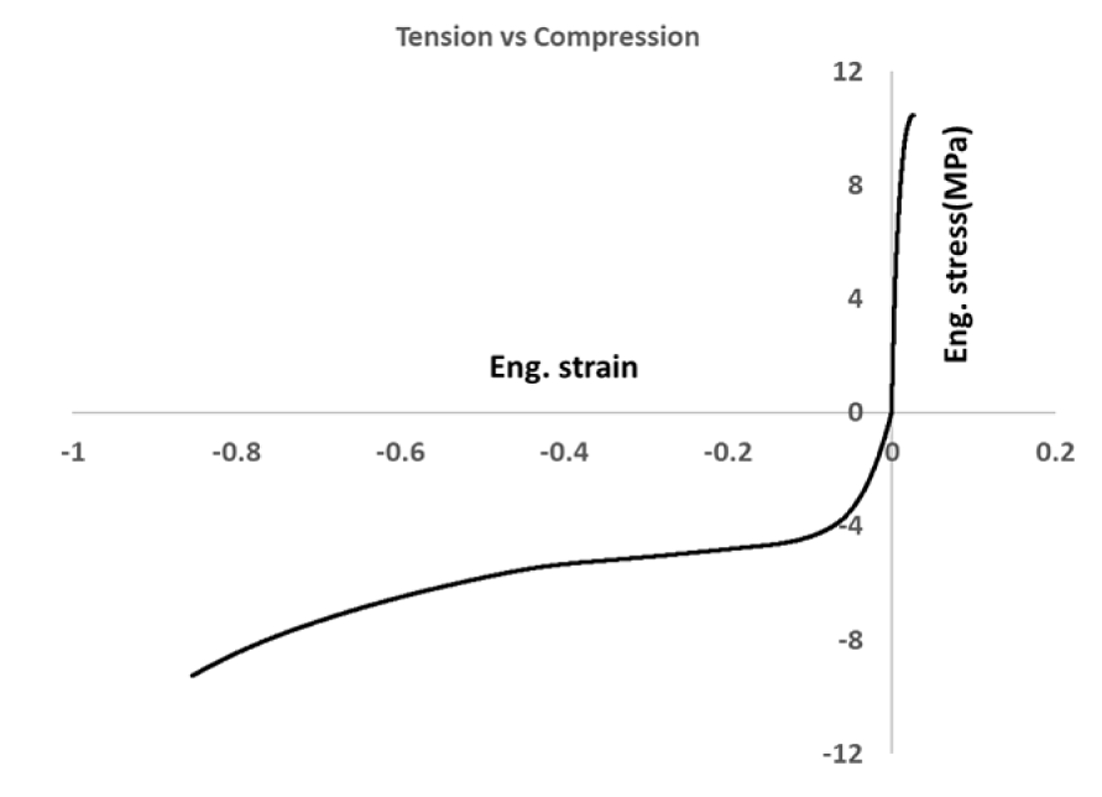
Fig. 7은 변형률 속도 0.01/s 조건에서 인장과 압축의 응력–변형률 선도를 비교한 결과로, 펄프몰드 소재가 인장과 압축에서 현저히 상이한 거동을 나타냄을 보여준다. 이러한 특성을 고려할 수 있는 구성방정식의 적용이 필요함을 확인하였다.
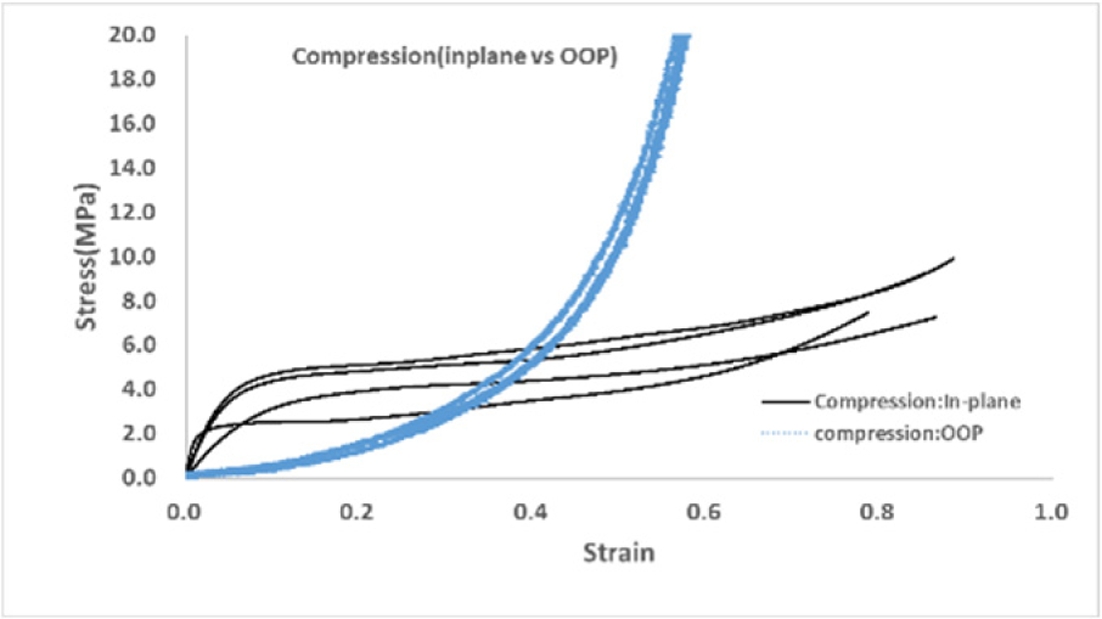
Fig. 8은 면내 압축과 두께 방향 압축 거동을 비교한 결과를 나타낸 것이다. 변형 초기에는 두께 방향 압축 강도가 상대적으로 낮게 나타나지만, 압축이 진행됨에 따라 소재의 밀도가 증가하면서 강도가 급격히 증가하는 거동의 차이가 확인된다. 이러한 두께 방향 압축에서의 급격한 강도 증가는 펄프몰드 제품의 보호 기능이 상실된 이후에 나타나는 특성으로 판단되므로, 본 연구에서 수행한 펄프몰드 제품의 충격 해석에서는 이를 고려하지 않았다.

낙하 충격시험기를 이용하여 펄프몰드 제품의 충격 실험을 수행하였다. 낙하 질량은 14 kg으로 모든 시험 조건에서 동일하게 유지하였으며, 충격 속도는 1 m/s와 2 m/s의 두 조건으로 설정하였다. 각 속도 조건에서 1차 충격을 가하여 하중–변위 데이터를 획득한 후, 변형된 시편에 대해 2차 충격을 추가로 가하는 방식으로 누적 충격 시험을 수행하였다.
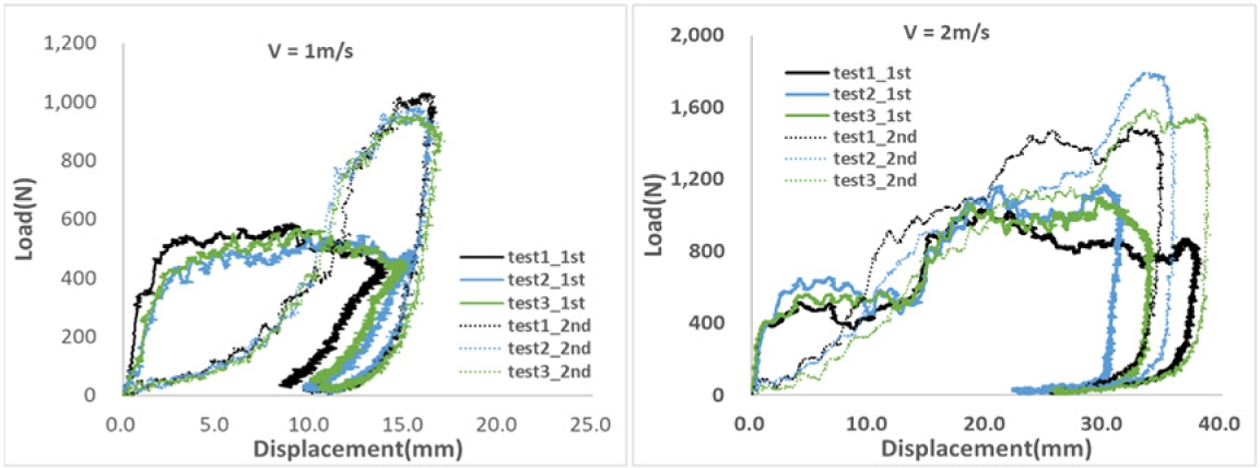
Fig. 9는 낙하 충격시험기와 충격 전·후 시편의 형상을 나타낸 것이며, Fig. 10은 시험 중 계측된 하중–변위 선도를 제시한다. 펄프몰드 제품은 일반적으로 단계적인 에너지 흡수가 가능하도록 설계되며, 본 시험에 사용된 제품의 경우 약 12 mm의 변형을 기준으로 1단계와 2단계 충격 에너지 흡수 구간으로 구분됨이 확인되었다.
충격 속도 1 m/s 조건의 누적 충격 시험에서는 시편의 전체 변형이 크지 않았으며, 일부 국부적인 파손이 관찰되었음에도 불구하고 충격 에너지 흡수 능력은 상당 부분 유지되는 것으로 나타났다. 하중–변위 선도 분석 결과, 1차 충격에서는 주로 1단계 에너지 흡수가 발생하였고, 2차 충격에서 2단계 변형이 진행되었음이 확인되었다.
충격 속도 2 m/s 조건의 누적 충격 시험에서는 1차 충격 단계에서 이미 2단계 변형까지 진행되었으며, 시편의 찢어짐과 같은 심각한 손상이 광범위하게 관찰되었다. 이에 따라 해당 조건에서는 1차 충격 이후 충격 에너지 흡수 능력이 대부분 상실되는 것으로 나타났다.

펄프몰드 소재의 물성 시험 결과, 인장과 압축 거동 간에 현저한 차이가 나타났으며 변형률 속도 효과 또한 뚜렷하게 관찰되었다. 이러한 펄프몰드 소재의 특성을 유한요소해석에 반영하기 위해, 본 연구에서는 LS-DYNA에서 제공하는 등방성 탄소성 물성 모델인 MAT_PLASTICITY_ COMPRESSION_TENSION 모델을 적용하였다. 본 재료 모델은 요소에서 계산된 압력의 부호에 따라 인장 및 압축 상태를 구분함으로써, 인장과 압축 거동의 차이를 고려할 수 있다. 또한 인장과 압축에 대해 서로 다른 탄성계수를 적용할 수 있으며, 변형률 속도 효과를 함께 고려할 수 있어 펄프몰드 소재의 재료 거동 특성을 효과적으로 반영할 수 있다.
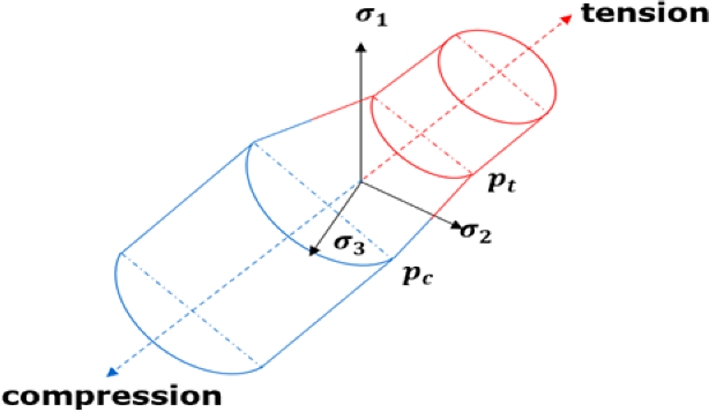
Fig. 11 및 식 (1)에 나타낸 바와 같이, 계산된 요소의 압력에 따라 인장 또는 압축 항복 곡선을 각각 적용할 수 있으며, 사용자가 정의한 천이 구간을 통해 해석의 안정성을 확보할 수 있다. 본 연구에서는 인장 임계 압력과 압축 임계 압력 값을 각각 0.3 MPa로 설정하여 해석을 수행하였다.



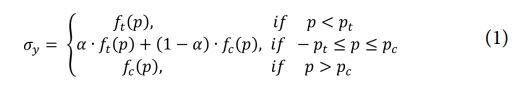
여기서 f_t(p)와 f_c(p)는 유효 소성 변형률에 따른 인장 및 압축 항복강도 곡선을 나타내며, p_t, p_c는 각각 인장 임계압력(tension cutoff pressure)과 압축 임계압력(compression cutoff pressure)을 나타낸다. 이때, α는 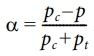로 정의된다[12].
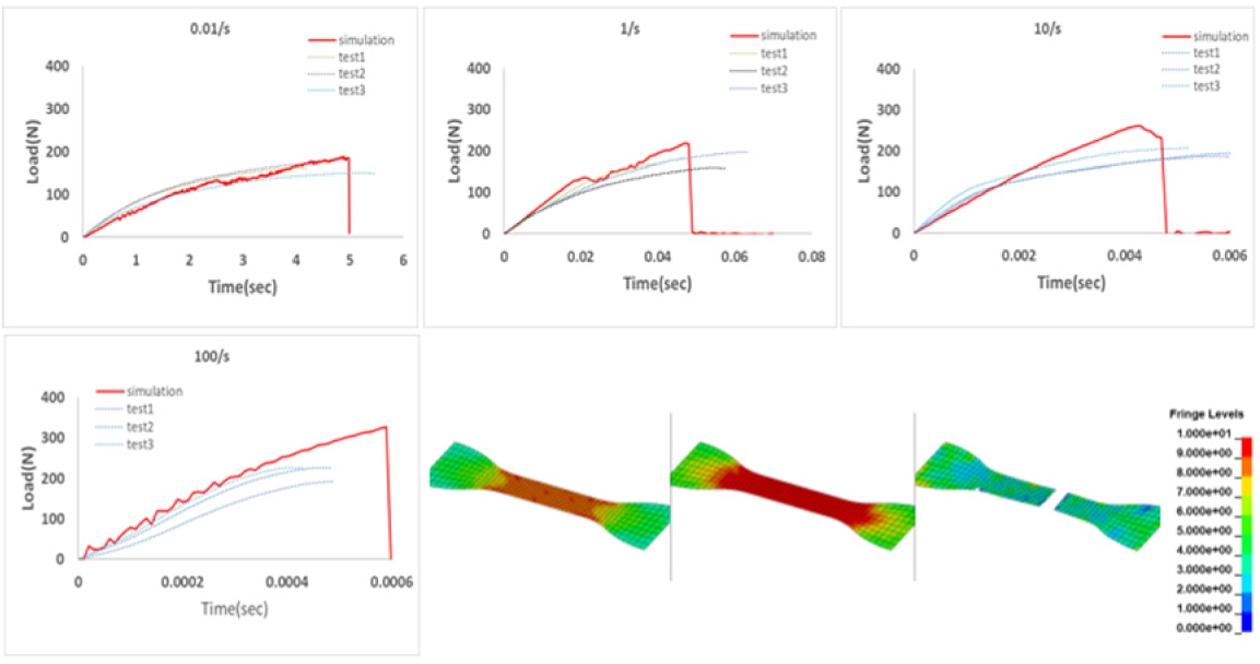
본 물성모델을 적용한 인장 시험 상관성 해석 결과, Fig. 12와 같이 시험 결과와 해석 결과가 높은 상관성을 보였으며, 이를 통해 LS-DYNA의 GISSMO 모델을 적용함으로써 파단 거동을 효과적으로 고려할 수 있음을 확인하였다.
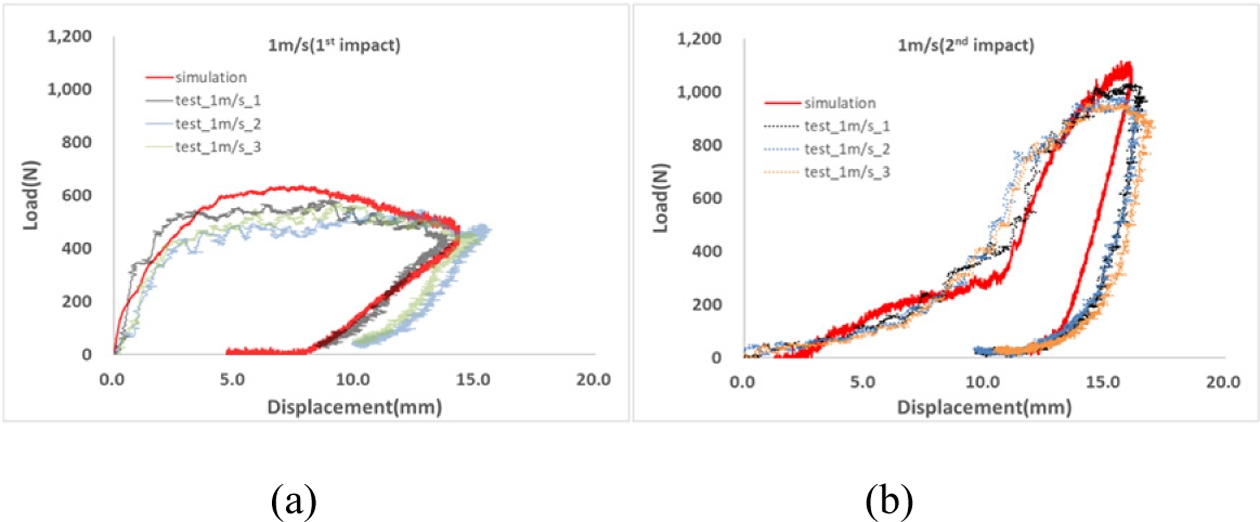
Fig. 13은 1 m/s 누적 충격 조건에 대한 해석 결과를 나타내며, MAT_PLASTICITY_COMPRESSION_TENSION 모델이 시험 결과와 높은 상관성을 보임을 확인할 수 있다. 누적 충격 해석의 경우, 1차 해석 결과를 2차 충격 해석의 초기조건으로 적용하여 해석을 수행하였으며, 그 결과 시험 결과와 해석 결과가 전반적으로 잘 일치하였다.
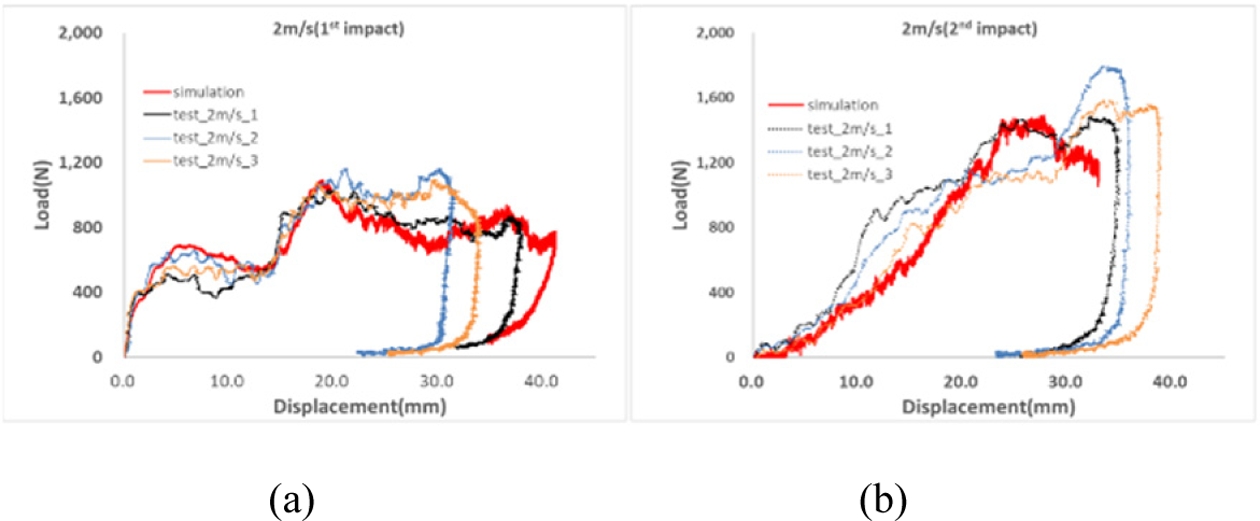
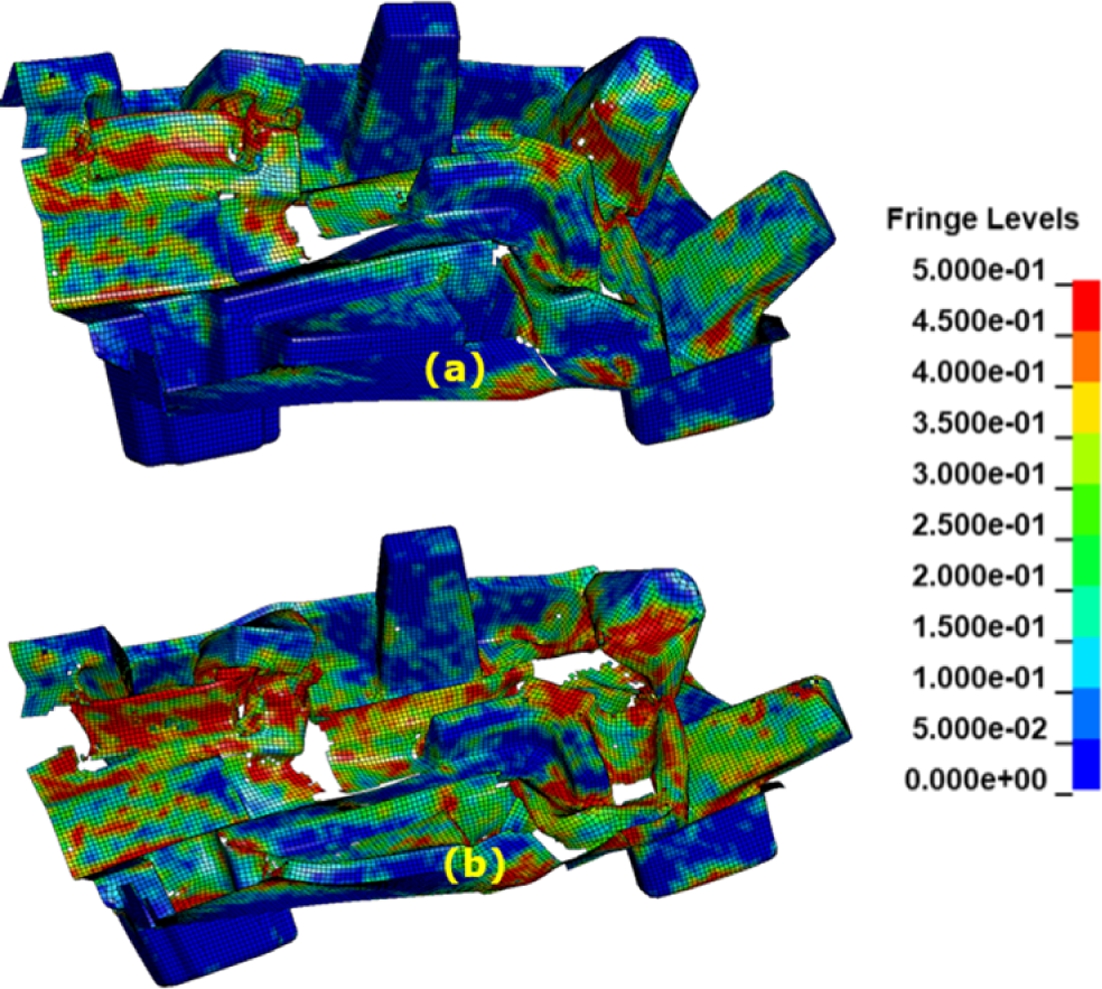
Fig. 14는 2 m/s 충격 조건에서의 하중–변위 선도에 대한 시험 및 해석 결과의 비교를 나타내며, 1차 및 2차 누적 충격 해석 결과 모두 시험 결과와 우수한 일치성을 보였다. 또한 Fig. 15와 Fig. 16에 나타난 바와 같이, 변형 형상과 GISSMO 모델을 이용한 파손 형태의 모사 결과 역시 실험 결과와 높은 상관성을 나타냈다.
MAT_PLASTICITY_COMPRESSION_TENSION 모델을 적용한 펄프몰드 소재의 유한요소해석 결과는 충격 실험 결과와 전반적으로 잘 일치하였다. 펄프몰드 제품의 완충 특성을 분석하기 위해서는 반복적인 누적 충격 거동을 고려할 필요가 있으며, 직전 충격 해석 결과를 다음 충격 해석의 초기조건으로 적용할 경우 실험 결과와 높은 상관성을 갖는 해석 결과를 얻을 수 있을 것으로 판단된다. 또한 본 모델은 GISSMO를 이용한 파단 거동의 고려가 가능하므로, 제품의 찢어짐 현상을 반영한 완충 능력 평가가 가능하다.

본 논문에서는 펄프몰드 소재의 충격 거동을 예측하기 위하여 LS-DYNA의 MAT_PLASTICITY_COMPRESSION_ TENSION 모델을 적용한 유한요소해석을 수행하고, 이를 낙하 충격 실험 결과와 비교·검증하였다. 1 m/s 및 2 m/s 충격 조건에서의 단일 및 누적 충격 해석 결과는 하중–변위 선도와 변형 형상에서 실험 결과와 전반적으로 잘 일치하였다. 특히 누적 충격 해석 시 직전 충격 해석 결과를 다음 충격 해석의 초기조건으로 적용함으로써, 반복 충격을 받는 펄프몰드 제품의 실제 거동을 보다 현실적으로 재현할 수 있음을 확인하였다.
또한 GISSMO 기반의 파단 모델링을 통해 충격 과정에서 발생하는 찢어짐을 고려한 완충 거동 평가가 가능하였으며, 이는 펄프몰드 제품의 에너지 흡수 능력과 구조적 안정성을 정량적으로 분석하는 데 유효함을 보여주었다. 따라서 MAT_PLASTICITY_COMPRESSION_TENSION 모델과 GISSMO를 결합한 유한요소해석 기법은 펄프몰드 소재 및 제품의 반복 충격 거동과 완충 성능을 신뢰성 있게 예측할 수 있는 해석 방법임을 확인하였으며, 향후 포장 설계 최적화 및 충격 안전성 평가에 효과적으로 활용될 수 있을 것으로 기대된다.

본 연구를 위한 2025년도 교육부 및 경상북도 지역혁신중심 대학지원체계(RISE)-(특화산업 Scale-up, 2025-RISE-15)의 지원에 감사드립니다.